复杂度分析
大O复杂度表示法
算法的执行效率,粗略地讲,就是算法代码执行的时间。我们知道所有代码执行的时间T(n)与每行代码的执行次数n成正比。
T(n)=O(f(n))
T(n)表示代码执行的时间;n表示数据规模的大小;f(n)表示每行代码执行的次数总和。公式中的O表示代码的执行时间T(n)与f(n)表达式成正比。
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度,简称为时间复杂度。当n很大时,你可以把它想象成10000,1000000。而公式中的低阶、常量、系数三部分并不会左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了。例如:以下两个简单例子。


时间复杂度分析
如何分析一段代码得时间复杂度,这里列举三个比较实用的方法。
只关注循环执行次数最多的一段代码
大 O 这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略公式中的常量、低阶、系数,只需要记录一个最大阶的量级就可以了。所以,我们在分析算法,代码的时间复杂度的时候,也只需要关注循环次数最多的那一段代码就可以了。这段核心代码执行次数的n的量级,就是整段代码的时间复杂度。
例如案例一,第2,3行代码都是常量级的执行时间,与n的大小无关,所以对于复杂度没有影响。循环执行次数最多的是第4,5行代码,所以这块代码要重点分析。这两行代码都是被执行了n次,所以子昂的时间复杂度是O(n)
加法法则:总复杂度等于量级最大的代码的复杂度

乘法法则:嵌套代码的复杂度等于其嵌套内外代码复杂度的乘积

几种常见时间复杂度实力分析

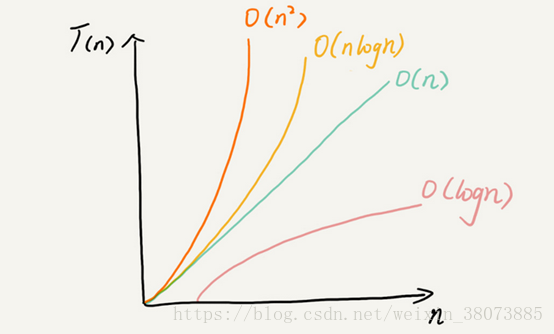
对于刚罗列的复杂度量级,我们粗略的分为两类,多项式量级和非多项式量级。其中非多项式量级只有两个:O(2n)和O(n!)
我们把时间复杂度为非多项式量级的算法问题叫做NP(Non-Deterministic Polynomial,非确定多项式)问题。
当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增加。所以,非多项式时间复杂度的算法其实是非常低效的算法。
1.O(1)
O(1)是一个常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。只要这样的代码的时间复杂度不随n的增长为增长,无论是执行1,10000,100000000次,它的时间复杂度都记作O(1).
小结:只要算法中不存在循环语句、递归语句,即使有成千上万的代码,其时间复杂度也是O(1)。
2.O(logn)、O(nlogn)

O(m+n)、O(m*n)
案例六

复杂度分析法则
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
空间复杂度分析
空间复杂度较之时间复杂度简单许多。
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。与此类似,空间复杂度全称是渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系。
案例七

浅析最好、最坏、平均时间复杂度
最好时间复杂度:代码在最理想情况下执行的时间复杂度。
最坏时间复杂度:代码在最坏情况下执行的时间复杂度
平均时间复杂度:用代码在所有情况下执行的次数的加权平均值表示。


利用之前的知识,得到的平均时间复杂度是O(n)
常见的时间复杂度
O(1)
int n=1/2/…/1000; // print(“*****”);
O(n)
for(int i=0;i<n;i++){ print(“*****”); }
O(n^2)
for(int i=0;i<n;i++){ for(int j=10;j<n;j++) print(“*****”); }
O(logn)
for(int i=1;i<n;i=i*2){ Println(“****”); }
O(2^n)又或者称为O(k^n)
for(int i=1;i>=Math(2,n);i++){ println(“***”); }
O(n!)
for(int i=1;i<=factorial(n);i++){ Println(“***********”); }