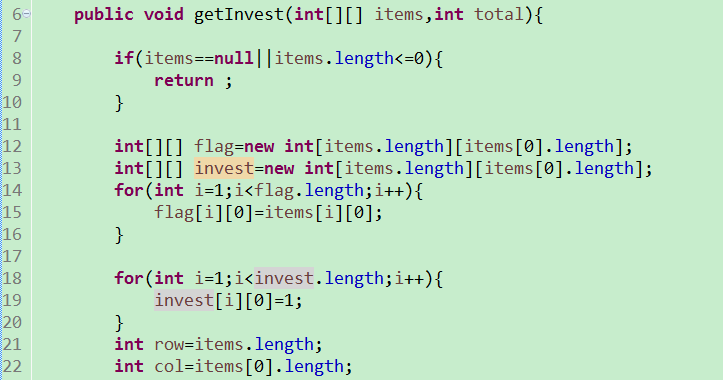
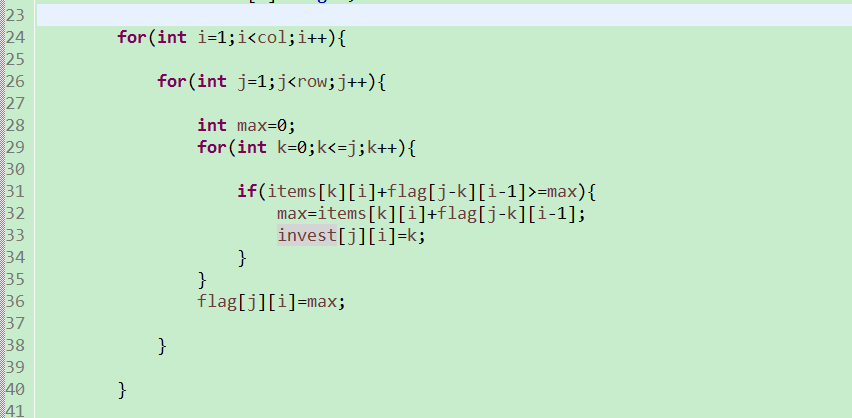
课件的内容来自于这位老师的课堂: https://www.youtube.com/watch?v=CalFvXOteNY&list=PLvdLBjhf_tgqq0ESrSd4rH8bXLmOlxN2J&index=3
以下的内容是我听课的笔记以及自己的理解,有错误或者争议的地方,欢迎 留言~共同学习,共同进步
投资问题的描述: fi(x)表示的是 把 x 元钱投资到第 i 个项目 所获得的收益。课堂上老师说,约束条件必须满足 投资的钱数 等于 总共的钱数,我认为应该是 小于或等于。继续往下面看。

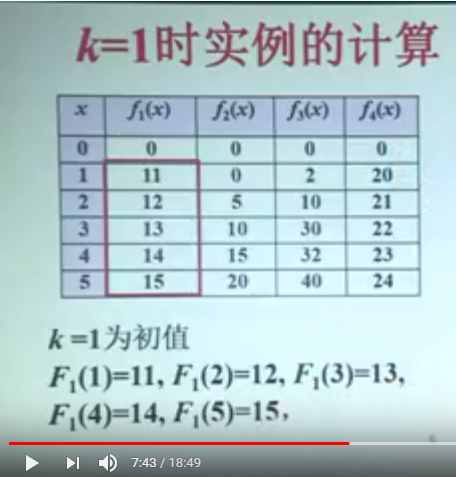
举例说明,更容易理解: 在这个表格中, 比如 坐标 (1,0)对应的值为11,这个含义就是说 把 1 万元投资到项目1中,获得的收益是 11万元。
坐标 (3,4)的值为 22, 这个含义就是说 把 3 万元 投资到 项目 4 中,获得的收益是 22万元。

子问题的界定:
k代表的含义是 ,你到底考虑到第几个项目
x代表的含义是: 你投资的钱数不超过 x
所以,这里的 k 和 x 是两个性质不同的参数。
我们之前学的矩阵链相乘, 问题中的 i ,j 是矩阵的下标。是同样类型的参数。
再讨论计算顺序, 先定下 所要投资的项目,是前 k 个,从1,2,3......k
当k 的值确定以后,再让 x 变化。比如,当k的值为5时,我们考虑 x 为1,2,3,4,。。。。。m 时,获得的收益。

优化函数的递推方程: Fk(x)表示的意思是 把 x 元 投资给 前 k 个项目 获得的最大收益。
x的范围(投资的总的钱数) 是0 到 x
k 的范围是 1 到 n (总共有 n 个项目)
那么 Fk(x) 的值应该是 对 第k个项目投资 了 xk 元 后的收益 + 把剩下的钱(x-xk)投给 前 k-1个项目的总的收益 Fk-1(x-xk)
那么,这个 xk的值 可以从 0 到 x,就是说,可以一分钱也不投资给 第k个项目,也可以把所有钱都投资给 这个项目,所以,这里要遍历 x+1次 才可以获得收益的最大值。

下面举例说明,当 k=1 时, 就是说 考虑前面 第一个 项目。只投资第一个项目。
把 0元投资给第一个项目,收益为0元,
把 1 元投资给第一个项目,收益为 11元
把 2 元投资给第一个项目,收益为 12 元,以此类推
举例说明,当K=2 时, 我们考虑把 钱投资给 前 2 个项目。
K确定以后,我们就要来遍历 x ,x是投资的总的钱数,范围是 从 0 到 5.
当 x= 5时,我们分析情况:
方案有 :(0,5),(5,0),(1,4),(4,1),(2,3),(3,2)
F2( x=5)=max{ f1(0)+f2(5) , f1(5)+f2(0) , f1(1)+f2(4) , f1(4)+f2(1) , f1(2)+f2(3) , f1(3)+f2(2) }
max { 0 +20 , 15+0 , 11 +15 , 14 +0 ,12 + 10 , 13+5 } ,所以,此时最大的收益是 26 万元。

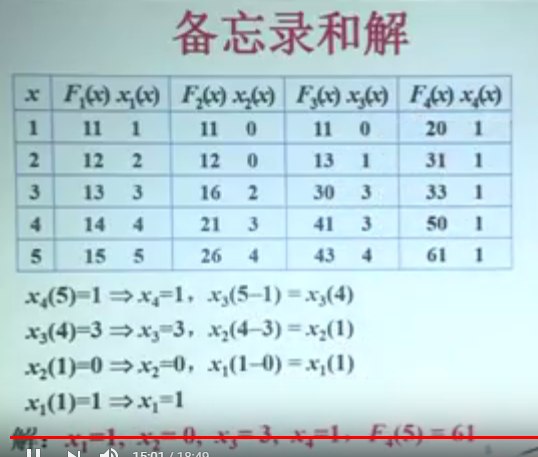
备忘录 和解:
F1(x )就是我们刚刚提到的, 把 x万元投在到 前 k 个项目中,这里 k=1
那么 , x 1(x) 是什么意思呢,这是标记函数, 表示的意思是, 你得到当前的最大收益时,你给了最后一个项目多少钱
比如 ,我们刚刚算的 F 2(5) ,我们把5万元投资到前 2 个项目中, 当获得最大收益 26 万元时, 我 们给第二个项目
投资的是4万元。 上面已经说的很清楚了。
那我们来举个不同的例子分析一下。
比如我要追踪 我投资 4万元给 这四个项目获得的最大收益,显然是 50万元。
此时,给第四个项目的投资是1 万元, x 4( 4)=1, 也就是说, x4=1,d第四个项目投资 1万元
x3(3)= 3, 也就是说,我们把剩余的3 万元全部投资给了 第三个项目
剩下的钱为 0 ,无法投资
时间复杂度分析:
有两种分析方法,



小结:

代码稍后加上! 感谢老师耐心的讲解,学到很多东西~