Q:怎么理解数据结构?
- 技术点:数据结构
- 思路:数据结构的定义、分类
- 参考回答:研究数据的逻辑结构和物理结构以及它们之间相互关系,并对这种结构定义相应的运算,而且确保经过这些运算后所得到的新结构仍然是原来的结构类型。
- 按照逻辑结构分类
- 线性结构:线性表、栈、队列
- 非线性结构:树、图
- 按照存储结构分为顺序结构、链式结构、索引结构、哈希结构
Q:什么是斐波拉契数列?
- 技术点:递归和循环
- 思路:斐波那契数列的定义
- 参考回答:斐波那契数列指的是这样的数列1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...即这个数列从第3项开始,每一项都等于前两项之和,数学表示F(1)=1,F(2)=1, F(3)=2,F(n)=F(n-1)+F(n-2)(n>=4,n∈N*)
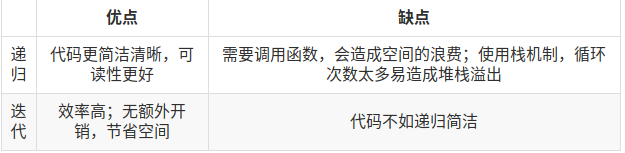
Q:迭代和递归的特点,并比较优缺点
- 技术点:递归和循环
- 参考回答:递归和迭代都是循环的一种,特点:
- 递归就是通过重复调用函数自身实现循环;满足终止条件时会逐层返回来结束循环
- 迭代通过函数内某段代码实现循环;使用计数器结束循环
Q:了解哪些查找算法,时间复杂度都是多少?

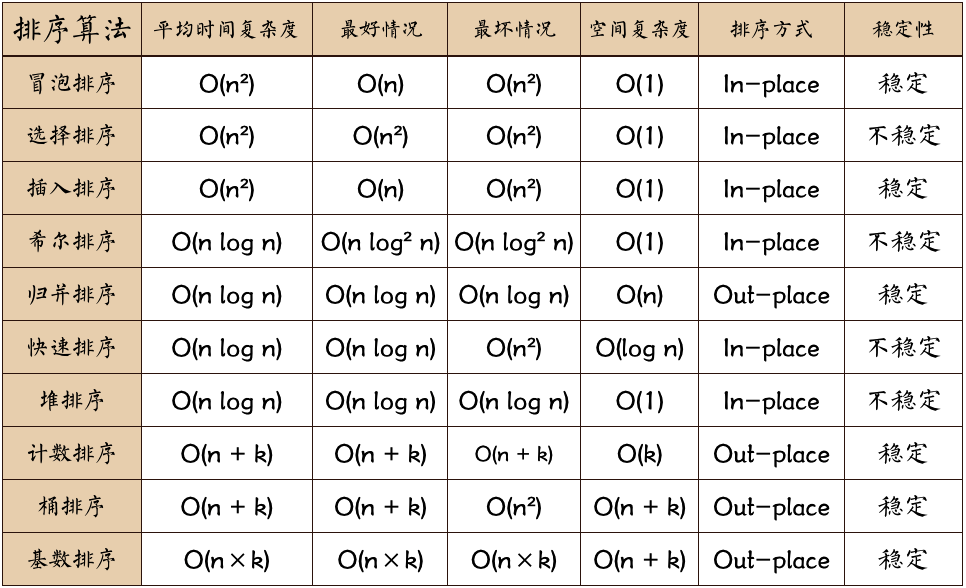
Q:了解哪些排序算法,并比较一下,以及使用场景
Q:二叉排序树插入或删除一个节点的过程是怎样的?
- 技术点:查找
- 参考回答:
- 二叉排序树插入操作:先查找该元素是否存在于二叉排列树中并记录其根节点,若没有则比较其和根节点大小后插入相应位置
- 二叉排序树删除操作:
- 待删除节点是叶子节点,直接删除即可
- 待删除节点是仅有左或右子树的节点 ,上移子树即可
- 待删除节点是左右子树都有的节点 ,用删除节点的直接前驱或直接后继来替换当前节点
Q:什么是红黑树?
- 技术点:查找
- 参考回答:红黑树是一种自平衡二叉查找树,包含性质:
- 节点是红色或黑色
- 根节点是黑色
- 叶子节点是黑色
- 每个红色节点的两个子节点都是黑色
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
Q:100盏灯问题
- 题目描述:问题描述:有100盏灯,编号依次为1,2,3.100,电灯全部关着。现在来了100个人,第一个人把所有的灯开关按下;第二个人隔一个灯按下(2,4,6…);第三个人每隔两个灯按下(3,6,9…).第100个人隔99个灯按下(100),最后还有几盏灯,那几盏灯亮着?
- 问题分析:
对于每个人在拉关开关就是将原来的变反。
现在第一个人走后,所有的灯全亮;
第二个人走后,2 的倍数的灭。。。。
以此类推。。。。。
- 对于每盏灯,拉动的次数是奇数时,灯就是亮着的,拉动的次数是偶数时,灯就是关着的。
- 每盏灯拉动的次数与它的编号所含约数的个数有关,它的编号有几个约数,这盏灯就被拉动几次。
- 1~100这100个数中有哪几个数,约数的个数是奇数。我们知道一个数的约数都是成对出现的,只有完全平方数约数的个数才是奇数个。
所以这100盏灯中有10盏灯是亮着的。
它们的编号分别是: 1、4、9、16、25、36、49、64、81、100。
它们的编号分别是: 1、4、9、16、25、36、49、64、81、100。
代码:
import java.util.*; public class test{ private static int count = 0; public static void main(String[] args) { int a[] = new int[100]; //100盏灯的状态 Arrays.fill(a, 0); for (int i = 1; i <= a.length; i++){ //100个人 for (int j = 0; j < a.length; j++){ //100盏灯 if ((j+1) % i == 0){ //第(j+1)盏灯对于被第i个人的行为后的状态。 if (a[j] == 0){ //原来的状态取反 a[j] = 1; }else{ a[j] = 0; } } } } for (int c : a){ if (c == 1){ count ++; } } System.out.println(count); } }
Q:海量数据问题
- 技术点:海量数据问题
- 思路:分治、哈希、bit、堆
Q:二分查找(手写)
public static int binarySearch(int[] a, int key){ int low, mid, high; low = 0; high = a.length - 1; //最大下标 while (low <= high){ mid = (high + low) / 2; //折半下标 if (key > a[mid]){ low = mid + 1; //关键字比折半值大,则最小下标调成折半下标的下一位 }else if (key < a[mid]){ high = mid - 1; //关键字比折半值小,则最大下标调成折半下标的前一位 }else{ return mid; } } return -1; }
Q:反转链表(手写)
- 技术点:链表
- 思路:
- 方法1:重复将首节点的下一个节点调整到最前面,如链表1->2->3->4,调整过程为2->1->3->4,3->2->1->4,4->3->2->1
- 方法2:递归,使链表从尾节点开始指向前一个节点
- 参考代码:
//节点类 public class ListNode{ int val; ListNode next = null; ListNode(int val){ this.val = val; } } //方法1 public ListNode reverseLinkedList(ListNode head){ if (head == null || head.next == null){ return head; } ListNode p = new ListNode(-1); //拟1个头节点 p.next = head; ListNode nextNode = head.next; while (nextNode != null){ //后一个节点调整到最前 head.next = nextNode.next; nextNode.next = p.next; p.next = nextNode; nextNode = head.next; } return p.next; } //方法2,递归 public ListNode reverseLinkedList(ListNode head){ if (head == null || head.next == null){ return head; } ListNode pNode = reverseLinkedList(head.next); head.next.next = head; head.next = null; return pNode; }
Q:用两个栈实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。(手写)
- 技术点:栈和队列
- 思路:
- 入队:将元素进栈A
出队:判断栈B是否为空,如果为空,则将栈A中所有元素pop,并push进栈B,栈B出栈, 反之栈B直接出栈
- 参考代码:
public class Solution{ Stack<Integer> stack1 = new Stack<Integer>(); Stack<Integer> stack2 = new Stack<Integer>(); //入队 public void add(int node){ stack1.push(node); } //出队 public int poll(){ if (stack1.empty(0 && stack2.empty())){ throw new RuntimeException("Queue is empty!"); } if (stack2.empty()){ while (!stack1.empty()){ stack2.push(stack1.pop()); } } return stack2.pop(); } }
- 技术点:线程同步
- 思路:加锁进行限制,并配合wait()和notifyAll()
- 参考代码:
private static char c = 'A'; private static int i = 0; public static void main(String[] args) { Runnable runnable = new Runnable(){ public void run(){ synchronized(this){ //加锁 try{ int threadId = Integer.parseInt(Thread.currentThread().getName()); while (i < 26){ if (i % 3 == threadId - 1){ System.out.println(threadId +""+ (char) c++); i++; notifyAll();// 唤醒处于等待状态的线程 }else{ wait(); //释放当前锁并进入等待状态 } } }catch(InterruptedException e){ e.printStackTrace(); } }//执行结束释放当前锁 } }; Thread t1 = new Thread(runnable, "1"); Thread t2 = new Thread(runnable, "2"); Thread t3 = new Thread(runnable, "3"); t1.start(); t2.start(); t3.start(); }
