使用教材:《learn you a Haskell》,中文1-8章戳我
准备工作。
编译器&调试器:安装Haskell Platform,也就是著名的GHC;
文本编辑器:
①安装Eclipse(最新的是4.2),安装EclipseFP,根据Extra configuration steps安装一些必要的插件;
②安装GVIM,调教一下_vimrc;
③安装leksah,虽然这是一个IDE,但是仍然需要和GHC配合工作;
④使用其他Editor,比如Emacs、Yi甚至notepad等;
其实像Haskell这种小众语言,还是用Vim或者Emacs更好一些,这里推荐一个已经调教好的VIM,里面已经修正了对haskell的一些支持,并且加入了补全系统。 不过如果写大的工程文件的话,个人感觉Eclipse更方便一些。
第一章 入门
Haskell的基本思想:高等抽象,不依赖于计算机模型。语法尽量接近数学上的表达式。
例如,在数学上一元函数表达式为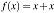 ,在haskell中对应的函数就是f x = x + x,除了将括号换成空格,其余都一样。二元函数也类似,
,在haskell中对应的函数就是f x = x + x,除了将括号换成空格,其余都一样。二元函数也类似,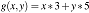 对应的Haskell函数也就表示为 g x y = x*3 + y*5,我们也可以定义
对应的Haskell函数也就表示为 g x y = x*3 + y*5,我们也可以定义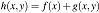 ,在Haskell中对应的也就是:h x y = f x + g x y,很明显具有形式上的一致性。
,在Haskell中对应的也就是:h x y = f x + g x y,很明显具有形式上的一致性。
条件函数:
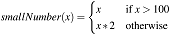
条件函数对应Haskell中的if语句,与其他编程语言不通但是与数学上的函数相同的是:每个if必须对应一个else,不可以省略。对于上述函数,这里的表达式显然是:
- smallNumber x = if x>100
- then x
- else x*2
在haskell中,如果一个函数没有参数,那么它是一个"定义",也就是其他语言中的"常量"(在ghci下使用关键字let来定义)。
为了书写的方便,可以通过使用`操作符将前缀函数变成中缀函数,例如div x y=x/y,在实际调用时可以写成 x `div` y。
另外需要注意的是,在Haskell中所有函数的首字母都不能大写。
List入门
list(序列)与其他语言中的array(数组)是相对应的,虽然在STL中list表示的是"链表"。list的特点:单类型,这点和array显然是一致的,不同的是list可以嵌套list,而且这些list的长度可以不同(类型必须相同)。list的表达形式如:[1,2],在方括号中放入元素,以comma分隔。字符(串)字面值的表达方式与C一致。字符串就是字符的list,所有适用于list的操作都可以直接用在字符串上。
list的特性比较像stack,可以使用 ++ 操作符进行pushback操作,但是haskell需要遍历整个list,效率很低。但是如果使用 : 操作符进行pushfront操作,速度就很快。需要注意的是++操作符的右表达式必须也为list,如果是单个元素,就放入[],而 : 操作符的左表达式必须为元素,如果需要插入多个元素,就按次序分开插入(:表达式的执行顺序是自右向左)。下标运算符!!,下标从0开始计算。list的比较方式同C中strcmp。
与C语言中array最大的不同之处在于list是haskell原生支持类型,也就是可以直接以"字面值"存在的类型,而C中的array必须以variable形式存在。所以在haskell中可以直接使用函数操作list,常用的几个函数:
head:返回头部;
tail:返回去掉头部的其他部分(尾部);
last:返回最后一个元素;
init:返回除了最后一个元素的其他部分;
length:返回长度;
null:检测是否为空;
reverse:反转序列;
take n list:从list中取前n个元素组成list,n>=0,如果n=0,得到一个空list;
maximum/minimum:得到最大/小元素(list中的元素必然可以比较);
sum:求和;
elem x list:判断x是否存在于list中;
区间
list的Range特性仍然是来源于数学,比如常数集{x},x取1到100,一般写作{x}={1,2,3..100},在list中也可以这么干,写出前两个元素确定step,两个点号表示range,最后是上/下界(由于计算机本身的限制,最好不要在浮点数中使用range特性)。如果不标上/下界的话,我们会得到一个无限长的list(显然这在数学上是合法的),haskell为了尽量与数学抽象一致,引入了"惰性求值"的特性,也就是说,haskell不会管这个无限长的list,只在你需要它的一部分时,再处理这个一部分。
生成list的一些函数:
cycle list:生成重复的无限长序列;
repeat n:生成仅含有n的无限长序列
replicate n x:生成含有n个x的序列
List comprehension
list comprehension来源于数学中的集合表达式,如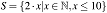 ,在haskell中表示为[x*2 | x <- [1,2..10] ].如果有多个条件,就用comma隔开,表示取所有满足条件集合的交集。例如
,在haskell中表示为[x*2 | x <- [1,2..10] ].如果有多个条件,就用comma隔开,表示取所有满足条件集合的交集。例如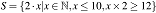 对应于[x*2 | x <- [1,2..10], x*2 >=12].在 | 左边是取值,右边是filter的条件。<-表示"属于",如果不关心取出的值,可以用_ <- []这种形式,可以省去一个变量名。对于嵌套的list类型,可以写出对应的嵌套list comprehension,用 | 隔开过滤条件。
对应于[x*2 | x <- [1,2..10], x*2 >=12].在 | 左边是取值,右边是filter的条件。<-表示"属于",如果不关心取出的值,可以用_ <- []这种形式,可以省去一个变量名。对于嵌套的list类型,可以写出对应的嵌套list comprehension,用 | 隔开过滤条件。
元组
Tuple(元组)与list的特性正好相反:每个tuple可以装不同类型的元素;两个tuple只有元素个数和对应次序的元素类型都相同时,才能视为同一类型。如果用C语言来比较的话,和一个defined的struct类型有行为上的一致性。如果要嵌套list和tuple,注意list要求类型的一致,而tuple类型一致的条件是很苛责的。tuple的表达行式是(x,y),括号内至少有两个元素,因为有一个元素没有什么意义(想一想只有一个元素的struct),空的tuple也就是()也算是一种类型。tuple不能增加或者减少元素,不同类型的tuple也不能相互比较。
只有两个元素的tuple通常称为pair(序对),和STL中的pair一致。pair常用的操作函数:
fst:返回首项;
snd:返回次项;
zip list1 list2:将两个list中的元素进行交叉配对,返回一个由pair组成的list;如果两个list中的元素个数不一致,以较短的那个为界;
第二章 类型与类型类
Haskell是静态类型语言,但是与C++或者java不同的是,haskell有类似动态语言中的自动类型推导特性(C++11中引入auto关键字后也有了此特性)。在ghci中可以使用:t 来解析表达式或者函数,返回形如 表达式::类型 的结构。其中 :: 符号表示类型约束,在声明函数时也可使用该符号来明确定义域和值域。
如:addThree :: Int->Int->Int->Int
addThree x y z= x+y+z
使用->符号分隔参数,返回值类型在最后(显然每个函数只能返回一个值)。常见类型包括:Char,Int,Integer(前者有界,后者无界但是效率不如前者),Float,Double,Bool。所有类型的首字母大写。
类型类,类型类的概念类似于java中的"接口",它规定了满足一系列特性的类的集合。常见的类型类包括:Eq(相等性),Ord(可比较性,返回LT、GT、EQ等),Show(可显示性,对应函数show),Read(与Show相反,对应函数read可以将字符串转为需要的类型,形式是read x ::type或者让read根据所在的表达式自己推断需要的类型如 read "3.5"+4),Enum(可枚举性,即可以用succ和pred得到后继或者前驱值),Bounded(有界性,可以使用minBound和maxBound函数获得上下界),Num(数字类型),Integral(整数类型),Floating(浮点类型)。
使用=>符号来声明类型类的约束,如fromIntegral :: (Integral a, Num b) => a -> b(这个函数用于将整数类转换成更通用的Num类型)
第三章 函数的语法
模式匹配
模式匹配的本质就是一大串swith…case,或者说if…else if…这些,遇到第一个匹配值后就会跳出该函数(有些类似C++中try…catch的匹配过程)。这里举著名的斐波那契数作为例子。我我们知道Fibonacci sequence的数学定义为

那么对应的Haskell代码为
- fibonacci :: ( Integral a) =>a->a
- fibonacci 0=0
- fibonacci 1=1
- fibonacci x=fibonacci (x-1) + fibonacci (x-2)
显然这段代码与公式(2)具有形式上的一致性。注意这里没有约束x>=0,所以匹配不是健全的。
对list进行模式匹配,常见的方法是将list分解为(x:xs),x匹配head,xs匹配tail,但是不能用++进行分割,原因很简单,因为++作用于list而不是元素。操作符@匹配全体引用,例如all@(x:xs),就意味着可以用all来代替(x:xs),这被称为as模式。
门卫
门卫(guard)是与模式匹配配合使用的,它的作用是增加过滤条件。对于区间匹配的条件函数,使用门卫是很简洁而恰当的。Guard的语法:在函数和=之间插入 | guard。
Where
关键字where用于在函数中进行变量或者函数的声明,一般放置在guard函数之后。在where函数中声明的辅助函数中可以嵌套使用where,这样就可以把一个复杂的表达式通过换元表达为几个符合的简单函数式。
完善上面的fibonacci函数,将第4行改为
- fibonacci x
- | x<0 = -1
- | otherwise = fibonacci (x-1) + fibonacci (x-2)
当然这里让x<0的时候返回一个负值并不是很恰当,不过这样不会有异常抛出了。
今天的复习就到这里:)