题意
给定 (n) 个点 (m) 条边的有向图,求出图中所有的强连通分量。
(n leq 25,m leq n(n-1))
题解
可以使用 (O(n)) 的 Tarjan 算法。
同样也可以使用更简洁的 Floyd 传递闭包。具体来讲,就是将普通 Floyd 松弛的过程 ( ext{dis}_{i,j} = min{ ext{dis}_{i,j}, ext{dis}_{i,k}+ ext{dis}_{k,j}}) 改为连通性判断。设 ( ext{f}_{i,j}) 表示 (i) 是否可以到达 (j),则松弛过程为 (f_{i,j}=f_{i,j} |(f_{i,k} & f_{k,j}))。其它和 Floyd 相同。
题意
给定 (n) 个点 (m) 条边的带权无向图,给定 (q) 组询问,每次询问两点间路径上边权最大的边的最小值。
(n leq 100,m leq 1000,q leq 10^4)
题解
将 Floyd 进行修改,松弛改为 (f_{i,j} = min{f_{i,j},max{f_{i,k},f_{k,j}}})。
题意
在三维空间中给定 (n) 个球形空间(可以相交)和两个点 (A,O)。在球形空间内部移动不消耗时间,否则每个单位距离需要 (10) 秒。求出从 (A) 到 (O) 的最短时间,答案保留整数。
(n leq 100),坐标、答案均在 ([-2^{31},2^{31}-1]) 范围内。
题解
(A) 和 (O) 可以看作半径为 (0) 的球形空间。然后对于这 (n+2) 个球形空间两两枚举建边,设球形空间 (i,j) 的距离为 ( ext{dis}),半径分别为 (r_i,r_j),那么:
- 当 ( ext{dis} leq r_i+r_j) 时,这两个球形空间相交或相切,可以不消耗时间地进行移动,建边 ((i o j,0))。
- 否则,建边 ((i o j, ext{dis} - r_i - r_j)),因为两球面距离即 两球心距离 (-) 两球半径。
以 (A) 为起点,(O) 为终点跑最短路,答案 ( imes 10) 即为答案。
题意
求 (n) 点 (m) 边带权无向图的最小环,输出环上的点,给出任意解均可。
(n leq 100,m leq 10000)
题解
求最小环是 Floyd 经典问题,不再赘述。这里来讲讲如何输出路径。
在求最小环时,中转点为 (k),那么最小环一定是 ( ext{mindist}(i,j) + (j o k) + (k o i)),其中 ( ext{mindist}) 表示两点间的最短路径。
我们可以在松弛的时候额外记录 (i,j) 两点的最短路中转点为 (k),如果最短路为 (i o j),那么中转点为 (0)。
然后,我们便可以递归求一条路径上经过了哪些点。
设计函数 (print(i,j)) 求出 (i) 到 (j) 的最短路径经过了哪些点。如果中转点为 (0),记录路径上经过点的数组 (p) 添加 (j),然后返回。否则,我们可以依次执行 (print(k,j)) 和 (print(i,k))((k) 为 (i,j) 两点最短路的中转点)。
观察到这样会让最外层的 (i) 被漏掉,所以手动补上即可。
题意
某个软件有 (n) 个错误,(m) 个补丁。每个补丁有四个集合 (B1_i,B2_i,F1_i,F2_i),当且仅当软件目前存在 (B1_i) 中所有错误,不存在 (B2_i) 中所有错误时,它会修复所有在 (F1_i) 中的错误,并加入在 (F2_i) 中的错误。使用每个补丁都需要花费时间。
求修复完所有错误最少需要的时间。
(n leq 20,m leq 100),答案不超过 (10^9)
题解
对软件当前的状态进行二进制压缩,第 (i) 位为 (1/0) 表示包含 / 不包含第 (i) 个错误。然后以最初状态为起点最短路即可,终点为状态 (0)。(2^{20}) 在 (10^6) 数量级,控制好常数即可通过。
题意
有 (n) 个火车站,还有 (m) 条经济线,(k) 条商业线,经济线和商业线均为双向路线。选择乘坐每一条路线都需要一定的时间。
只能坐最多一次商业线(可以不坐),但经济线可以坐无数次。求从火车站 (s) 到 (e) 的最短时间。
- (n leq 500,1 leq s,e leq n)
- (m,k leq 1000)
对于每个点 (i) 拆成两个 ((i,0)) 和 ((i,1)),分别表示在点 (i),没有坐 / 坐了商业线的最小时间。
对于一条 (u o v) 的经济线,建 ((u,0) o (v,0)) 和 ((u,1) o (v,1)) 两条边。商业线只需要建 ((u,0) o (v,1)) 一条边。
以 ((s,0)) 为起点最短路,记最短路为 ( ext{dis}),(min{ ext{dis}_{(e,0)}, ext{dis}_{(e,1)}}) 即为答案。
题意
给定 (n) 点 (m) 边的带非负权无向图。一个人要从点 (1) 到点 (2),他只会选择经过满足如下条件的边 ((u,v)),然后从 (u) 走到 (v):
- 记 ( ext{fdis}_i) 为点 (2) 到点 (i) 的最短路
- 边 ((u,v)) 需要满足 ( ext{fdis}_u > ext{fdis}_v)
求有多少种不同的路径。
(n leq 1000),边权 (leq 10^6)
题解
首先以 (2) 为起点,求出 ( ext{fdis})。然后将所有满足条件的边 ((u,v)) 建成一个新的 DAG(根据题意,新图显然满足 DAG 的定义),DAG 上 DP 即可。
题意
有 (n) 部电梯和 (100) 层楼,编号从 (0) 到 (99) 层。第 (i) 部电梯升降一层需要 (T_i) 秒。每部电梯只停靠一部分楼层。
在同一层换乘电梯需要 (60) 秒,为了使问题简单,要换乘的电梯在 (60) 秒内一定能赶到所在楼层,但要换乘的电梯必须在该楼层停靠。
在 (0) 层可以马上上电梯,不需要等待。
求从 (0) 层到 (k) 层需要花费的最少时间。
题解
拆点,((i,j)) 表示人在第 (i) 层的第 (j) 部电梯内。对于每部电梯,将其停靠的楼层依次连边,边权为楼层差 ( imes T_i)。对于每一层,将所有停靠该层的电梯两两连边,边权为 (60)。
因为在 (0) 层可以马上上电梯,且停靠 (0) 层的电梯可能有多个,所以需要建立虚拟源点 (S),将其和每一个停靠 (0) 层的电梯连边,边权为 (0)。
以 (S) 为起点跑最短路,答案即为 (minlimits_{电梯 i 停靠 k 层} ext{dis}_{(k,i)})。
题意
给定 (n) 点带权无向图,求平均值最小的环。
(n leq 50),边权 (leq 10^7)
题解
考虑二分答案。对于二分的值 (x),将所有边权减去 (x) 后最短路,如果出现负环,则存在平均值小于 (x) 的环。正确性是显然的。
题意
给定 (n) 行 (m) 列的矩阵 (w_{i,j})。给定非递减的 (t_1,t_2,...,t_T),对于每个 (t_i),求出有多少个 (w_{i,j} > t_i) 的点组成的四连通块。
(n,m leq 1000,T leq 10^5,t_i leq 10^9)
题解
随着 (t_i) 的增加,(w_{i,j} > t_i) 的点渐渐减少。可以删点、维护连通性的 LCT 并不好写,但可以加点、维护连通性的并查集要好写的多。考虑倒序处理,并查集维护即可。
题意
有一棵 (n) 个叶子的无权树,给出叶子间两两的距离,复原这棵树,输出每个非叶节点的度数。
(n leq 50)
题解
将 (1) 作为根考虑。首先确定 ([1,2]) 这一条链。然后对于后面的每一个叶子,枚举树中当前存在的非叶节点并判断当前要考虑的叶子是否能成为该节点的子孙。显然,这样的节点是唯一的。不断地填充非叶节点,构造出一条新的链。
填充非叶节点时顺便维护度数即可。
但代码实现较为困难,有许多要注意的小细节。

题意
给定 (52) 个点,(n) 条边的图。编号 (leq 26) 的点为城市,反之为乡镇。你携带着货物,要从 (S) 到 (T)。
进入城市的时候,需要交付身上 (dfrac{1}{20}) 的货物(向上取整),进入乡镇时,需要交付 (1) 个货物。
到达 (T) 时,你至少需要携带 (p) 个货物。问出发时至少需要带多少货物。
- 最坏是完全图,
- 答案超过 (2^{31}-1)
- (1 leq S,T leq 52,S eq T)
题解
从 (T) 出发最短路。记 ( ext{dis}_i) 表示从 (i) 出发到 (T) 至少要带的货物,那么对于边 (u o v),如果 (u) 是乡镇(注意是 (u)),那么边权为 (1),反之边权为 (left lceil dfrac{ ext{dis}_u}{19} ight ceil)。
这个玩意显然可以 Dijkstra 跑出来。也许可以二分然后从起点开始跑,然而我写挂了...
题意
给定各点连接如下的 (n imes m) 点阵,求左上角到右下角的最小割。
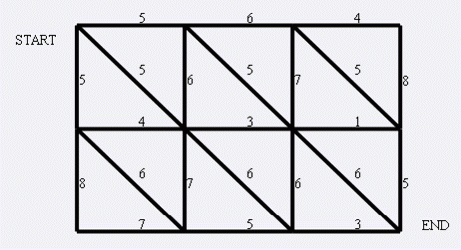
出处为 ICPC-Beijing 2006 狼抓兔子 题面。
(n,m leq 1000)
题解
可以网络流,但 LA / UVA 上会 TLE。
考虑将原图转对偶图,然后最短路即可。即:
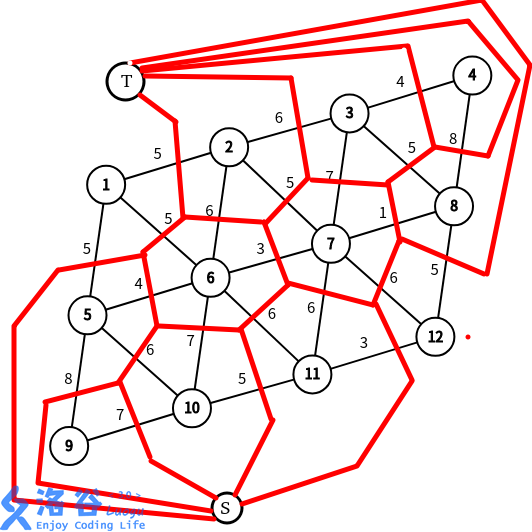
出处 https://www.luogu.com.cn/blog/Imakf/solution-p4001。感谢原作者 Imakf。

