HDU2196
树的直径:树上最远两点(叶子结点)的距离。
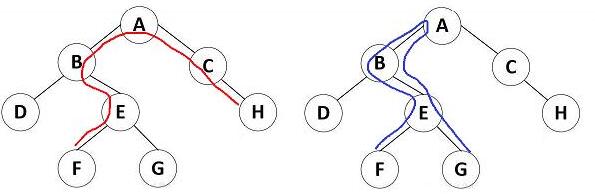
方法一:暴力求解,从每个点开始遍历图,可以得到每个点v所在的最长路径max1和次长路径max2,注意的是最长路径和次长路径除了点v没有其他公共结点。如下图所示,经过点A的最长路径应该是下图左所示的路径,而非下图右所示的路径,通过A的最长路径必须是来自不同分支。方法一,暴力破解,每个点做一趟DFS的话,时间复杂度为(O(n^2))
方法二:从树上任意点u开始DFS(BFS)遍历图,得到距离u最远的结点v,然后从v点开始DFS遍历图,得到距离v最远的结点w, 则v、w之间的距离就是树的直径。
证明:假设路径v-w为树的直径
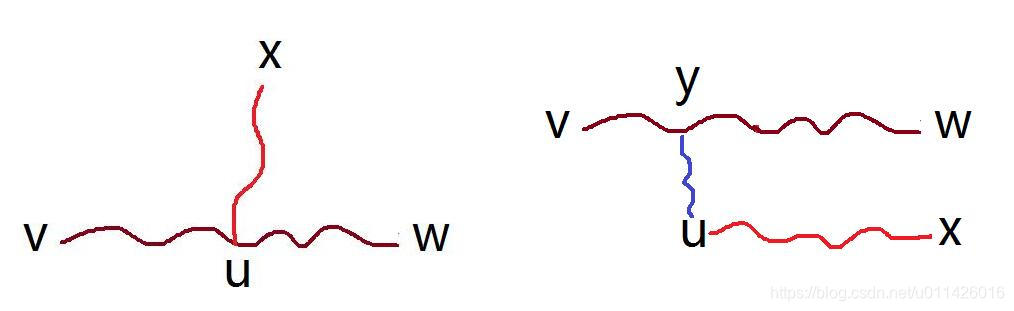
1)u位于v-w所在的路径上,如下图左图所示,那么从u点做DFS能访问到的最远点必然是v或w, 否则假设访问到的最远点为x, 如下图所示,有(,dist(u,x) geq dist(u,v), dist(u,x) geq dist(u,w))分两种情况讨论:
a) 如果只取大于号, (dist(u,x)>dist(u,v) ,dist(u,x)>dist(u,w)),
那么(dist(u,x)+dist(u,v)=dist(v,x)>dist(u,v)+dist(u,w)=dist(v,w)), 那么v-w不是树的是直径,跟假设矛盾。
b) 如果取大于等于号,(dist(u,x) geq dist(u,v) , dist(u,x)geq dist(u,w))
假设(dist(u,x) = dist(u,v))那么(dist(x,w)=dist(v,w)), 这样也没问题,树的直径不唯一而已,那么x依然位于树的直径的一个端点上。
2)u不位于v-w所在的路径上,如下图右图所示,那么有 (,dist(u,x)>dist(u,y,v),dist(u,x)>dist(u,y,w)),这里y是u到路径[v-w]的任意点,那么就有 (dist(u,x)+dist(u,y,w)=dist[x,w]>dist(v,y)+dist(y,w)=dist(v,w)), 那么说明那么v-w不是树的是直径,跟假设矛盾。
综上,方法二正确,且复杂度为2趟DFS,因此复杂度为(O(n))。比方法一快很多。
#include <iostream>
#include <cstring>
using namespace std;
//maxv:源点能到的最远点,maxdis:最远点对应的距离,
const int maxn = 1e4 + 5;
struct Edge { int to, next, w; }edges[2 * maxn];
int head[maxn], maxdis,maxv, ne;
void add(int u, int v, int w) {
edges[ne] = { v, head[u], w };
head[u] = ne++;
}
//u:dfs的源点,f: u点的父节点,d2s:u点到源点的距离
void dfs(int u, int f, int d2s) {
if (maxdis < d2s){
maxdis = d2s;
maxv = u;
}
for (int e = head[u]; e != -1; e = edges[e].next) {
int v = edges[e].to, w = edges[e].w;
if (v == f) continue; //父节点已经访问过,防止重复遍历,相反孩子不会重复遍历。
dfs(v, u, d2s + w);
}
}
int main() {
int e, u, v, w, s;
cin >> e;
memset(head, -1, sizeof(head));
for (int i = 1; i <= e; i++) {
cin >> u >> v >> w;
add(u, v, w), add(v, u, w);
}
dfs(1, -1, 0); //从结点1开始遍历,找到最远点maxv及对应的最远距离maxdis
maxdis = 0;
dfs(maxv, -1, 0);//从结点maxv开始遍历,找到最远点对应的距离maxdis
cout << maxdis << endl;
return 0;
}
给一棵树,有n个结点,结点之间的边有权值,问每个结点的最远结点距离其多远 介绍一个定义:树的直径指的是树上两个最远点对。
题解
求法1:任取点u,找到离他最远的点v,然 后再找离v最远的点w,则((v,w))为直径。
求法2:维护dp[u][0/1]为u子树内以u为端点 的最长路/次长路,答案就是 dp[u][0]+dp[u][1];
我们还有一个定理,对于树上任意一个点 它的最远点对必定为直径两个点之间的一个。 故复杂度三次dfs
P1077
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共(m)盆。通过调查顾客的喜好,小明列出了顾客最喜欢的(n)种花,从(1)到(n)标号。为了在门口展出更多种花,规定第(i)种花不能超过(a_i)盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试计算,一共有多少种不同的摆花方案。
题解
f[i][j]表示我取了前(i)种花,拿了(j)盆花的方案,则
f[i][j]+=f[i-1][j-k](0<=k<=ai)
#include<bits/stdc++.h>
using namespace std;
const int maxn=105, mod = 1000007;
int n, m, a[maxn], f[maxn];
int main()
{
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
f[0] = 1;
for(int i=1; i<=n; i++)
for(int j=m; j>=0; j--) //注意,是01背包
for(int k=1; k<=min(a[i], j); k++)
f[j] = (f[j] + f[j-k])%mod;
cout<<f[m]<<endl;
return 0;
}
未AC原因:
可能这题是个背包。我错了orz
P2014
https://www.luogu.com.cn/problem/U53204
现在有 (N) 门功课,每门课有个学分,每门课有一门或没有直接先修课(若课程a是课 程b的先修课即只有学完了课程( ext A),才能学习课程( ext B))。一个学生要从这些课程里选择( ext M)门课程学习,问他能获得的最大学分是 多少?
题解
树形背包O(nm)的做法
我们把原树叫做 A。
定义 多叉树的后序遍历指的是:在搜索某个结点的过程中,先记录它的所有子树,再记录它本身。注意,如果有多个子树,则后序遍历的顺序不限。
定义 多叉树的后序遍历序列指的是在上述过程中所记录下来的序列。
我们不妨在 DFS 后把结点按照后序遍历序列重新编号。下图就是一个例子,左图为原树 A,右图为重新编号的树 B。
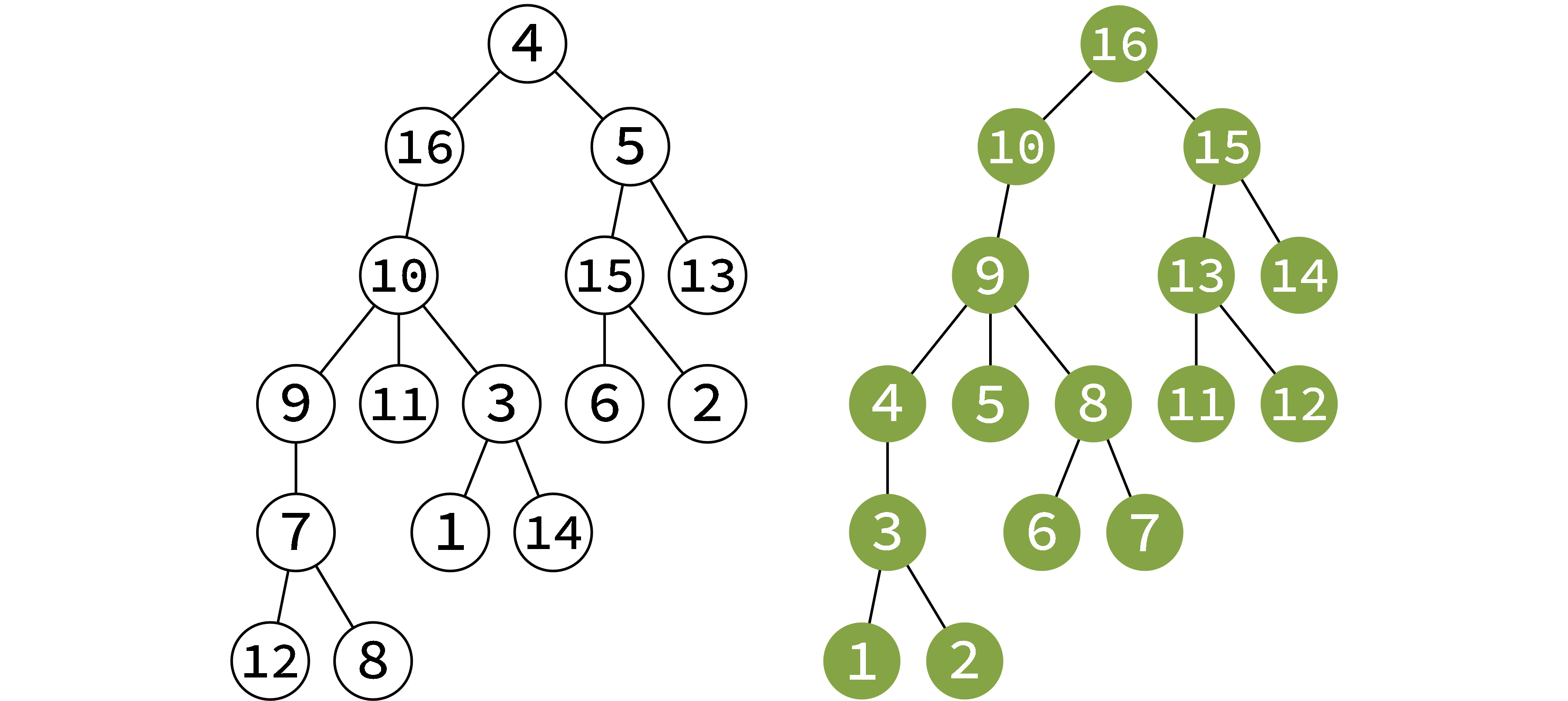
现在,如果我们要复制一棵树 B(不妨称复制品为 C),将新树 B 里面的结点按编号(也就是按照 A 树的后序遍历序列)依次加入 C 中,我们会发现,每次加入的结点在当前情况下都是根结点。下图展示了放入 4, 7, 8, 9 号结点时,新图的情况。
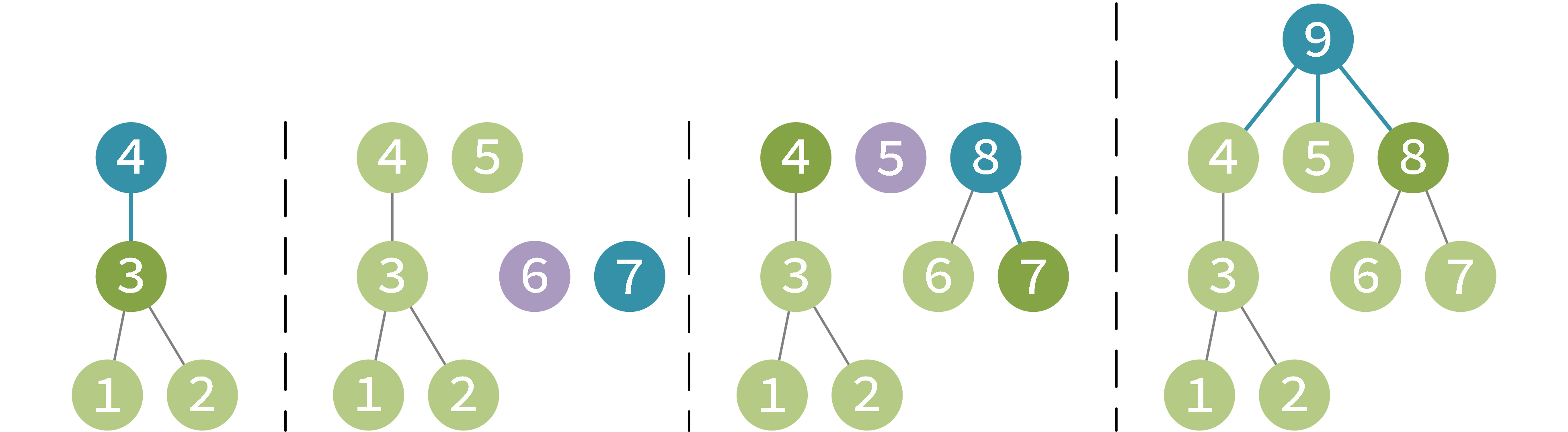
因此,设 (mathrm{dp}(i,j))表示将树 B 的结点 (1ldots i)放入新图,背包容量为 jj 时,所能取得的最大价值。设 (mathrm{size}_i)表示以 (i)为根的子树的大小。
若取物品 (i),则可以取它的子树,则
问题转化为「将结点 (1ldots i-1)加入 C,且背包容量为 (j-1)时,所能取到的最大价值」加上物品 (i) 的价值,
所以答案为 (mathrm{dp}(i-1,j-1)+v_i)
若不取物品 (i),则不可以取它的子树,则
问题转化为「将『结点 (1ldots i-1)中不属于 (i)的子树的结点』加入 C,背包容量不变时,所能取到的最大价值」
答案为 (mathrm{dp}(i-mathrm{size}_i,j))
综上可得 (mathrm{dp}(i,j)=max(mathrm{dp}(i-1,j-w_i)+v_i,;mathrm{dp}(i-mathrm{size}_i,j)))
易证其时间复杂度为 (O(NM))。
#include<iostream>
#include<cstdio>
#define maxn 1000
using namespace std;
int n,m,f[maxn][maxn],head[maxn],cnt;
struct edge
{
int to,pre;
}e[maxn];
inline int in()
{
char a=getchar();
while(a<'0'||a>'9')
{
a=getchar();
}
int t=0;
while(a>='0'&&a<='9')
{
t=(t<<1)+(t<<3)+a-'0';
a=getchar();
}
return t;
}
void add(int from,int to)
{
e[++cnt].pre=head[from];
e[cnt].to=to;
head[from]=cnt;
}
void dp(int now)
{
// f[now][0]=0;
for(int i=head[now];i;i=e[i].pre)
{
int go=e[i].to;
dp(go);
for(int j=m+1;j>=1;j--)
{
for(int k=0;k<j;k++)
{
f[now][j]=max(f[now][j],f[go][k]+f[now][j-k]);
}
}
}
}
int main()
{
n=in(),m=in();
for(int i=1;i<=n;i++)
{
int fa=in();
f[i][1]=in();
add(fa,i);
}
dp(0);
printf("%d
",f[0][m+1]);
return 0;
}
未AC原因:
情况讨论错了。DFS序需要复习。