目录
前言
目标: 掌握神经网络的基本概念, 学习如何建立神经网络(包含一个深度神经网络),以及如何在数据上面训练他们,最后将用一个深度神经网络进行辨认猫。
(1)了解深度学习的概念
(2)了解神经网络的结构,使用算法并高效地实现
(3)结合神经网络的算法实现框架,编写实现一个隐藏层神经网络
(4)建立一个深层的神经网络(一般把层数大于等于3的神经网络称为深层神经网络)
第一周(深度学习引言)
Deep Learning:
改变(应用):网络搜索和广告推荐
很好的示例:读取X光图像、精准化农业、自动驾驶等
突破:计算机视觉(图像识别),语音识别(机器翻译)
观点: 认为AI是最新的电力,大约在一百年前,我们社会的电气化改变了每个主要行业,从交通运输行业到制造业、医疗保健、通讯等方面,我认为如今我们见到了AI明显的令人惊讶的能量,带来了同样巨大的转变。
什么是神经网络?
我的初步理解:给定原始输入数据,按照特定的计算规则传递给神经元,后续经过相应的计算规则继续传递给下一层神经元,当到达最后一层时,得到的神经元中存储的数据即为需要输出的数据。
简单描述: 尝试输入一个x,即可把它映射成y。
例如,课程中给的关于预测房屋价格的神经网络示例,如下图:
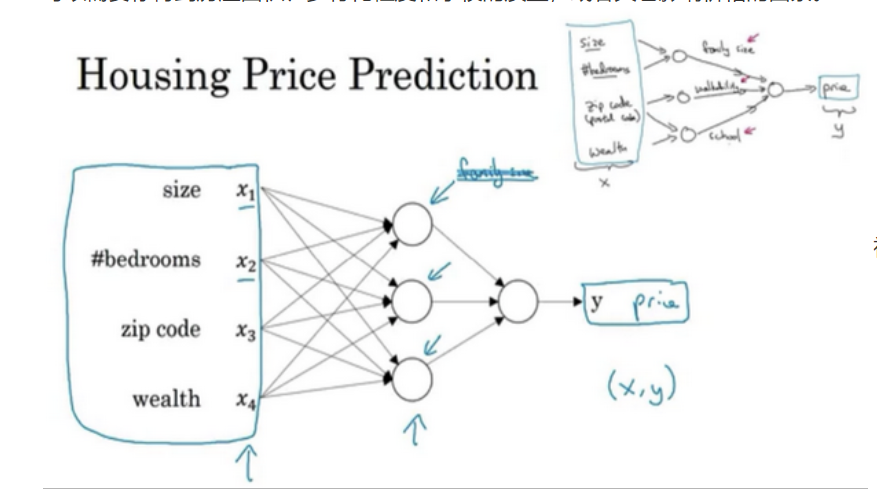
区分结构化数据和非结构化数据:
结构化数据: 数据的基本数据库, 例如在房价预测中,你可能有一个数据库,有专门的几列数据告诉你卧室的大小和数量,这就是结构化数据。
非结构化数据: 如音频,原始音频或者你想要识别的图像或文本中的内容。
什么是监督学习?
我的理解:给定大量得输入数据,以及对应得输出结果标记数据。来训练神经网络得到中间计算出对应输出结果的模型函数。成功得到该模型后,后续就可以使用该模型来预测新的输入数据的预测结果,从而得到实际价值。
简单描述:监督式学习的目标是在给定一个 (x, g(x))的集合下,去找一个函数g。
深度学习兴起条件:
- 可以获得更多的数据
- 硬件性能的提高,比如GPU
- 计算能力大大提高
- 激活函数的选择(从sigmoid函数转换到一个ReLU函数,是神经网络应用方面的一个巨大突破。因为在进行梯度下降计算时, sigmoid函数的梯度会接近零,所以学习的速度会变得非常缓慢,因为当你实现梯度下降以及梯度接近零的时候,参数会更新的很慢,所以学习的速率也会变的很慢。然而,使用ReLU函数恰恰解决这一问题)
第二周(神经网络的编程基础)
对于本周学习的内容,需要着重理解一下几个概念及背后的实现原理:
- 梯度下降
- 逻辑回归
梯度下降:
在逻辑回归算法第三步中需要使用梯度下降法,来求取代价函数J(w, b)的最小值。
梯度下降一个简单暴力的理解:在一个函数图像中沿着函数值不断减小的梯度方向下降(向下走)叫梯度下降。此处可见参考资料[1]
现在问题是要求取J(w, b)的最小值,可以看下面一个形象化的图像:
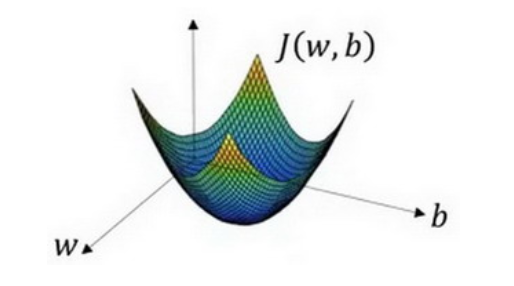
在这个图中,横轴表示你的空间参数w和b。要求J(w, b)最小值,即要求取图中曲面最低部的一点处的值即为最佳值。可以看出大小是按照梯度不断下降的方式变化。
对参数w的梯度下降更新公式(其中a是学习率,用来控制步长。:=表示更新参数):
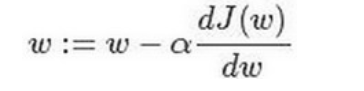
对参数b的梯度下降更新公式:
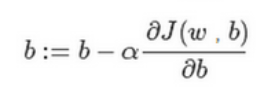
逻辑回归算法:
该算法分为三部分,分别是预测函数部分、损失函数、梯度下降法求取代价函数的最小值。此处可见参考资料[2]
首先说一下预测函数:
给定输入数据x,传递过程中的特征权重w和偏差b,计算最终的输出预测值y,这就是预测函数需要做的事情。
一般情况下,z = wx + b,你会发现函数z是一个线性函数,而且z值得大小依据x的取值大小而不断变化,不能给神经网络的最终预测结构提供帮助。
例如,识别一张猫的图片,最终的预测结果只有两种:不是,是。因此,我们可以类似处理,把最终输出的预测值y变为0和1两种,0表示是,1表示不是。
那么如何让z转化为最终的预测值y呢?
此处可以选择采用具有二分特性的sigmoid函数,sigmoid函数图像如下:
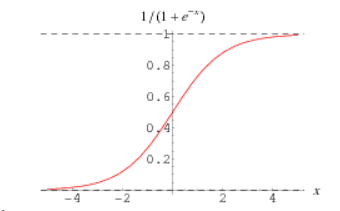
可以看出sigmoid函数的取值区间为(0,1),当x趋近正无穷大时,值趋近1,当x趋近负无穷大时,值趋近0。
那么我们可以把z值当作参数传递给sigmoid函数,如果sigmoid(z) >= 0.5就令y = 1, 否则令y = 0。
但是,逻辑回归做的处理是给出最终的估计值sigmoid(z),具体y的值大小是神经网络最后一步的最终输出结果。(PS:注意预处理函数此处给出的示例是sigmoid函数,对应其他情况需要选择其他合适的预处理函数)一般把y^ = o(z)(PS:这里是使用有y^表示数学字符y帽,o表示预处理函数)
总结,预测函数计算步骤:
z = wx + b, y^ = o(z),其中o是预处理函数。
损失函数:
损失函数又叫做误差函数,用来衡量算法的运行情况,Loss function:L(y^, y).
我们通过这个L称为的损失函数,来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中我们不这么做,因为当我们在学习逻辑回归参数的时候,会发现我们的优化目标不是凸优化,只能找到多个局部最优值,梯度下降法很可能找不到全局最优值,虽然平方差是一个不错的损失函数,但是我们在逻辑回归模型中会定义另外一个损失函数。
我们在逻辑回归中用到的损失函数是:
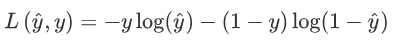
代价函数:
为了衡量算法在全部训练样本上的表现如何,我们需要定义一个算法的代价函数,算法的代价函数是对m个样本的损失函数求和然后除以m:
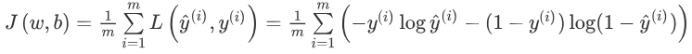
损失函数只适用于像这样的单个训练样本,而代价函数是参数的总代价,所以在训练逻辑回归模型时候,我们需要找到合适的w和b,来让代价函数J 的总代价降到最低。
最后,看几处课程中比较重要的几张图:
单个样本逻辑回归梯度下降计算过程:
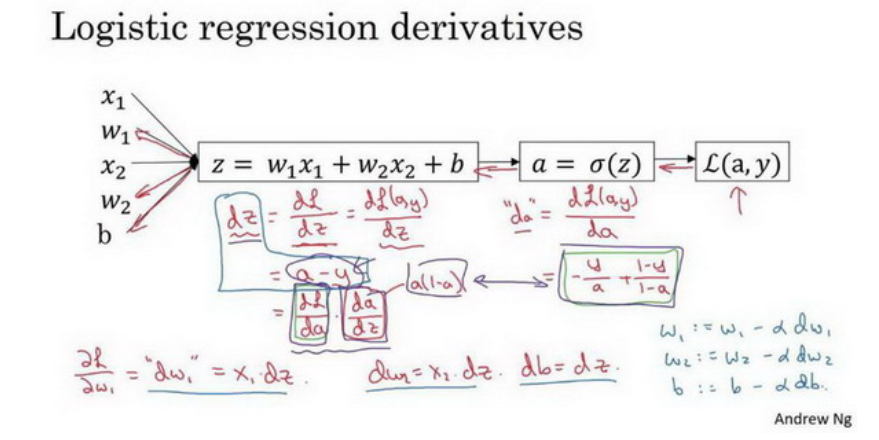
多个样本逻辑回归梯度下降计算过程:

第三周(浅层神经网络)
基于逻辑回归重复使用了两次及以上该模型就可得到神经网络,例如下图:
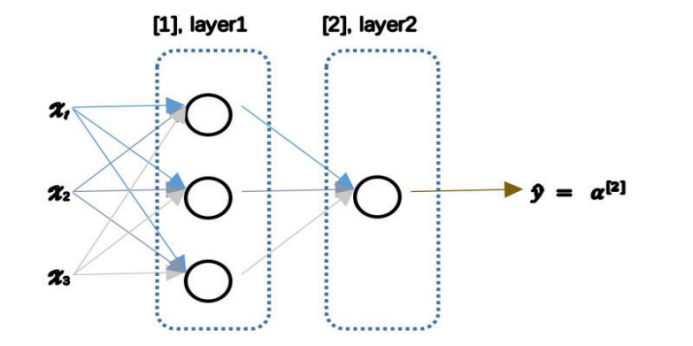
用圆圈表示神经网络的计算单元,逻辑回归的计算有两个步骤,具体如下图:
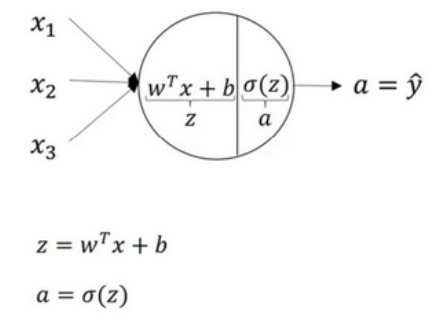
常见的激活函数:
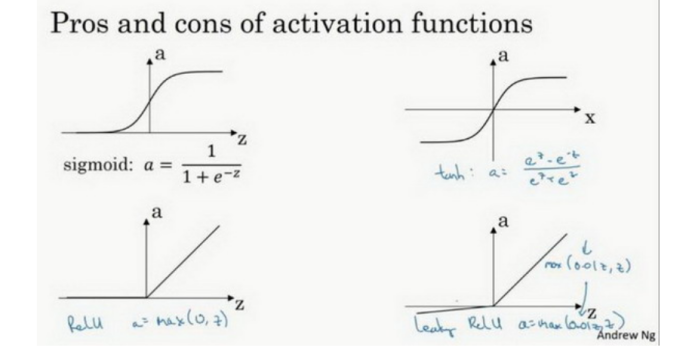
为什么需要非线性激活函数?
如果你使用线性激活函数或者没有使用一个激活函数,那么无论你的神经网络有多少层一直在做的只是计算线性函数,所以不如直接去掉全部隐藏层。(PS: 如果你是用线性激活函数或者叫恒等激励函数,那么神经网络只是把输入线性组合再输出。)
总而言之,不能在隐藏层用线性激活函数。 唯一可以用线性激活函数的通常就是输出层;除了这种情况,会在隐层用线性函数的,除了一些特殊情况,比如与压缩有关的,那方面在这里将不深入讨论。在这之外,在隐层使用线性激活函数非常少见。
当你训练神经网络时,权重随机初始化是很重要的。对于逻辑回归,把权重初始化为0当然也是可以的。但是对于一个神经网络,如果你把权重或者参数都初始化为0,那么梯度下降将不会起作用。
如果你要初始化成0,由于所有的隐含单元都是对称的,无论你运行梯度下降多久,他们一直计算同样的函数。这没有任何帮助,因为你想要两个不同的隐含单元计算不同的函数,这个问题的解决方法就是随机初始化参数。
第四周(深层神经网络)
有一个隐藏层的神经网络,就是一个两层神经网络。记住当我们算神经网络的层数时,我们不算输入层,我们只算隐藏层和输出层。
在做深度神经网络的反向传播时,一定要确认所有的矩阵维数是前后一致的,可以大大提高代码通过率。
为什么使用深层表示?
深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西。比如你录在音频里的单词、词组或是句子,然后就能运行语音识别了。同时我们所计算的之前的几层,也就是相对简单的输入函数,比如图像单元的边缘什么的。到网络中的深层时,你实际上就能做很多复杂的事,比如探测面部或是探测单词、短语或是句子。
想要你的深度神经网络起很好的效果,你还需要规划好你的参数以及超参数。
什么是超参数?
比如算法中的learning rate a(学习率)、iterations(梯度下降法循环的数量)、L(隐藏层数目)、n[l](隐藏层单元数目)、choice of activation function(激活函数的选择)都需要你来设置,这些数字实际上控制了最后的参数W和b的值,所以它们被称作超参数。
参考资料:
[1]https://blog.csdn.net/songhaoaa/article/details/48085083
[2] https://blog.csdn.net/ligang_csdn/article/details/53838743