看完郝斌老师的数据结构,特来做做笔记(有写的不好的地方请大佬指教)
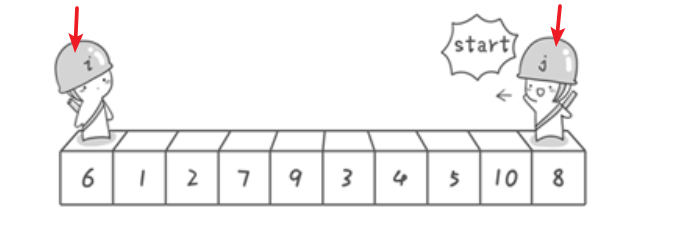
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序,将这10个数存入数组a[10],这个时候我们要设置一个临时变量val = a[0]
不一定是a[0],随便一个数都可以。
我们选中这个一个数val 是为了求出在排完序后val的真正位置,即val左边的数都小于val ,val 右边的数都大于val。
我们要研究的就是这个。
设定两个位置 i,j。分别存储数组元素的第一个和最后一个。
步骤:
让j所指的元素的值和i所指的元素的值比大小,
情况1:若a[j] < a[i] 则将 a[i]=a[j]
然后i位置+1
情况2:若a[j] > a[i] ,则将j位置左移,直到找到一个位置满足a[j] < a[i],将 a[i]=a[j]
然后再i位置+1
基于两种情况,我们分析一下:
初始位置:i = 0,j = 9;
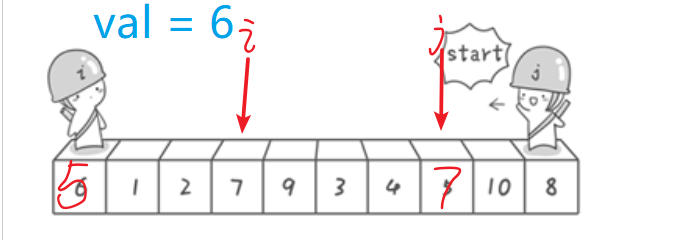
令val = a[i]
比较a[j]<val,否,此时将j--
再次比较,a[j]<val. 否,此时j--
再次比较,a[j] <val,此时将 a[i] = a[7] = 5;此时 j的位置在7位置
然后:
比较a[i] >val ,5不大于6,否,继续i++;
比较a[i] >val ,1不大于6,否,继续i++;
比较a[i] >val ,2不大于6,否,继续i++;
比较a[i] >val ,发现7大于6,a [3] >val,此时将a[j] = a[3],即a[7] = 7;
此时i的位置为3即a[3] = 7
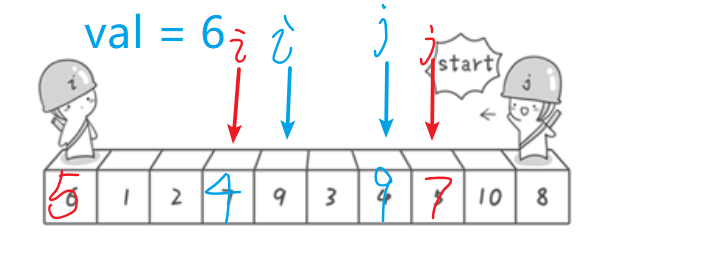
此时 i =3,j = 7;
比较a[j] < val 否,继续j--
比较a[j] <val 是,则将 a[i] = a[6],此时a[3] = a[6] = 4,j的位置此时为6
然后:
比较a[i] > val ,4不大于6,否,i++
比较a[i] >val 是,则将a[j] = a[i] 此时a[j] = 9,i的位置为4
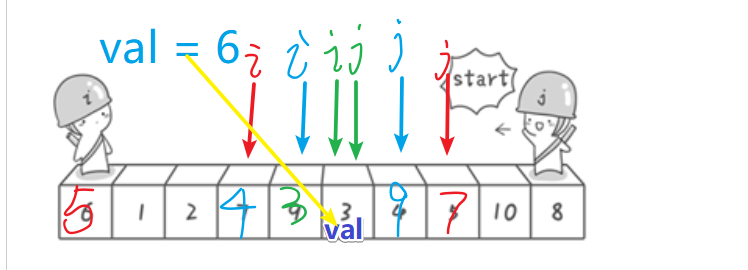
此时 i = 4,j=6
同理我们接着比较a[j] <val,9不小于6,j--
a[j]<val ,3小于6,所以 a[i] = a[j] =3,此时j的位置5,i的位置为4
然后
比较a[i] > val ,3不大于6 ,i++
此时a[i] = a[j] 终止比较。令a[i] = a[j] =val
比较到现在,我们只进行了一轮就将数组一分为二,确定了val的位置了。也可以发现在val左边的数都是小于val,右边的数都是大于val的。
利用递归的思想,重复以上步骤就可以将数组进行排序。
代码:
1 #include<stdio.h>
2 #include "stdafx.h"
3
4 int FindPos(int* a,int low,int high);
5 void QuickSort(int* a,int low,int high);
6
7 void QuickSort(int* a,int low,int high){
8
9 while(low < high){
10 int pos = FindPos(a,low,high);
11 //一分为二
12 QuickSort(a,low,pos-1);
13 QuickSort(a,pos+1,high);
14 }
15 }
16
17 //查找基数位置
18 int FindPos(int* a,int low,int high){
19
20 int val = a[low];
21 while(low < high){
22 while(low < high && a[high] >= val){
23 high--;
24 }
25 a[low] = a[high];
26
27 while(low < high && a[low] <= val){
28 low++;
29 }
30 a[high] = a[low];
31
32 }
33
34 a[high] = val;
35
36 return low;
37 }
38
39 int main(){
40
41 int a[10] = {2,4,1,5,7,9,11,24,70,12};
42
43 QuickSort(a,0,9);
44
45 for(int i=0;i<10;i++)
46 printf("%d ",a[i]);
47 printf("
");
48
49 return 0;
50 }
快速排序的算法复杂度分析:
快速排序的时间性能取决于快速排序递归的深度,可以用递归数来描述算法的执行情况。如图9-9-7,它是{50,10,90,30,70,40,80,60,20}快排的递归过程。
由于我们第一个数是50,正好是待排序序列的中间值,因此递归数是平衡的,此时的性能也比较好。
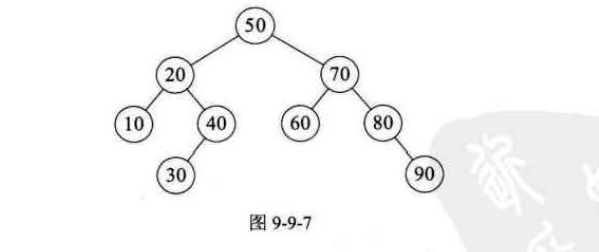
最坏的情况是,当待排序列是逆序或或者正序时,每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。如果递归树画出来,将是一颗斜树。

最优的情况下,第一次对整个数组扫一下,做n次比较,然后获取枢纽后将数组一份为二,那么各自还需要T(n/2)的时间,这个时间是最好的情况下的时间,所以平分两半,
以此类推,我们有了下面不等式的推断:

平均的情况:设置枢轴的关键位置在k上(1<k<n),那么
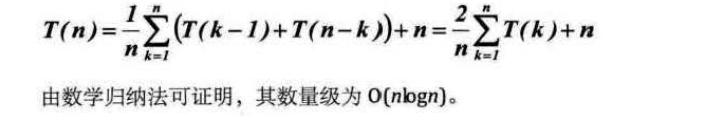


性能的优化
1、优化选取的枢轴val
由于上面我们选择的val = a[0] 刚好是整个数列集合的中间位子。所以可以将大小数一分为二。但是如果我们的a[0]不是一个中间位置的数呢?
如数组{9,1,5,8,3,7,4,6,2},这个时候如果把 val = a[low] ,low = 0,会是怎么样的呢?
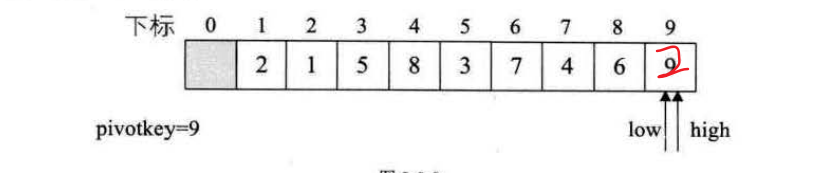
这个时候就发现low++了好多次,但是没有实质性的改变,像是在做无用功。
所以这种选择枢轴偏大数会影响程序的性能,选择偏小也一样。
那我们如何解决这个问题呢?我们可以选择介于偏大和偏小的数之间即可。这个数怎么找呢?
我们可以这样取头,中,尾三个元素进行排序,将中间数作为枢轴。这个办法称为三数取中法。
即在选择枢轴前面加上代码
1 //查找基数位置
2 int FindPos(int* a,int low,int high){
3
4 int m = low +(high-low)/2; //计算中间下标
5 /*比较大小*/
6 if(a[low] > a[high]){
7 swap(&a[low],&a[high]); //交换左与右端的数据,保证左端较小
8 }
9 if(a[m] > a[high]){
10 swap(&a[high],&a[m]); //交换中间与右端的数据,保证中间较小
11 }
12 if(a[m] > a[low]){
13 swap(&a[low],&a[m]); //交换中间与左端的数据,保证左端较小
14 }
15 /*此时low的位置即为三个数的中间位置的值了*/
16
17 int val = a[low]; //这边存在缺陷
18 while(low < high){
19 while(low < high && a[high] >= val){
20 high--;
21 }
22 a[low] = a[high];
23
24 while(low < high && a[low] <= val){
25 low++;
26 }
27 a[high] = a[low];
28
29 }
30 a[high] = val;
31 return low;
32 }
注意我们求枢轴的方法,但是当数据比较多的时候,那么枢轴的选取将变得更加重要,常见的有9数取中法,原理和3数取中类似。
这里就把快排的一些知识点写完了,快排是最常见的排序算法之一,也是难点之一,须重点掌握。
全部代码实现:

1 #include<stdio.h> 2 3 int FindPos(int* a,int low,int high); 4 void QuickSort(int* a,int low,int high); 5 void swap(int* low,int* high); 6 7 void QuickSort(int* a,int low,int high){ 8 9 if(low < high){ 10 11 int pos = FindPos(a,low,high); 12 //一分为二 13 QuickSort(a,low,pos-1); 14 QuickSort(a,pos+1,high); 15 } 16 } 17 18 //查找枢轴位置 19 int FindPos(int* a,int low,int high){ 20 21 int m = low +(high-low)/2; //计算中间下标 22 /*比较大小*/ 23 if(a[low] > a[high]){ 24 swap(&a[low],&a[high]); //交换左与右端的数据,保证左端较小 25 } 26 if(a[m] > a[high]){ 27 swap(&a[high],&a[m]); //交换中间与右端的数据,保证中间较小 28 } 29 if(a[m] > a[low]){ 30 swap(&a[low],&a[m]); //交换中间与左端的数据,保证左端较小 31 } 32 /*此时low的位置即为三个数的中间位置的值了*/ 33 34 int val = a[low]; //这边存在缺陷 35 while(low < high){ 36 while(low < high && a[high] >= val){ 37 high--; 38 } 39 a[low] = a[high]; 40 41 while(low < high && a[low] <= val){ 42 low++; 43 } 44 a[high] = a[low]; 45 46 } 47 a[high] = val; 48 49 return low; 50 } 51 52 53 void swap(int* low,int* high){ 54 int t =0; 55 t = *low; 56 *low = *high; 57 *high = t; 58 } 59 int main(){ 60 61 int a[10] = {2,4,1,5,7,9,11,24,70,12}; 62 63 QuickSort(a,0,9); 64 65 for(int i=0;i<10;i++) 66 printf("%d ",a[i]); 67 printf(" "); 68 69 return 0; 70 }
小结:
分治法的基本思想是:将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。
快排比较复杂,特别是复杂度的计算(这个我还是有点懵)和性能的优化,希望自己学习到后面的时候可以理解(迭代学习),可能是自己的数学功底不好,啧啧啧,先留个![]() 吧!!
吧!!
借鉴图片:
https://blog.csdn.net/adusts/article/details/80882649
参考资料:
《大话数据结构》
郝斌视频讲解:https://www.bilibili.com/video/av6159200?from=search&seid=9738629568092698275
