二叉树的三种遍历
链式二叉树又称二叉链表,遍历有三种,分别是前序(先序),中序,后序。
首先创建二叉树,没有建立,何谈遍历?
定义二叉树的存储结构为链式存储
1 typedef struct BiNode{
2 int data;
3 BiNode *lchild,*rchild; //左孩子和右孩子
5 }BiNode;
6 typedef struct BiNode* BiTree;
我们往往在创建之前要先初始化一下
1 /*初始化并建立二叉树*/
2 int index=0;
3 void CreateBiTree(BiTree* T,char data[]){
4 *T =NULL; //初始化为空
5 char ch;
6 if(index<strlen(data)){
7 ch = data[index++];
8 }else{
9 return;
10 }
11 if(ch =='#') //此节点为空
12 *T =NULL;
13 else{
14 *T = (BiTree)malloc(sizeof(BiNode));
15 if(!*T)
16 exit(0);
17 (*T)->data=ch; //生成根节点
18 CreateBiTree(&(*T)->lchild,data);
19 CreateBiTree(&(*T)->rchild,data);
20 }
21 }
先序
先序: 1.访问根结点
2.访问左子树
3.访问右子树
总结三个字:中左右


1 /*先序遍历*/ 2 void PreOrderTraverse(BiTree T){ 3 if(T ==NULL) 4 return; 5 printf("%c ",T->data); 6 PreOrderTraverse(T->lchild); 7 PreOrderTraverse(T->rchild); 8 }
中序
中序:1.访问左子树
2.访问根结点
3.访问右子树
总结三个字:左中右
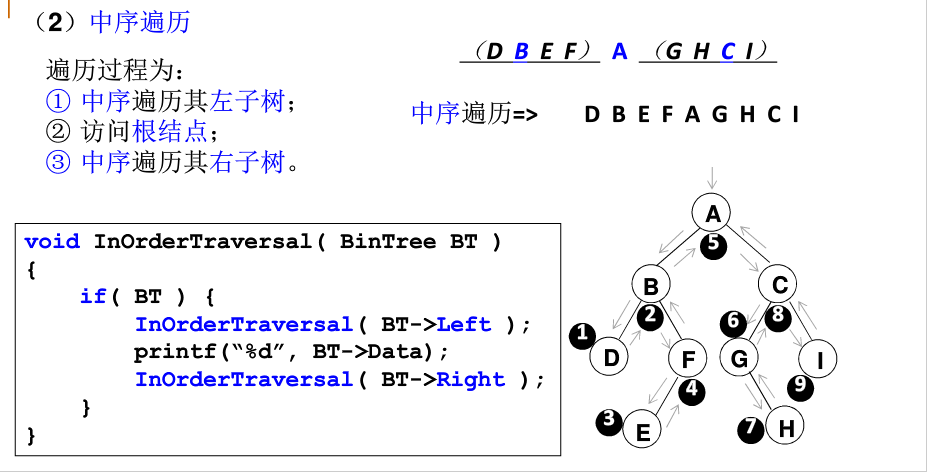

1 /*中序遍历*/ 2 void InOrderTraverse(BiTree T){ 3 if(T ==NULL) 4 return; 5 InOrderTraverse(T->lchild); 6 printf("%c ",T->data); 7 InOrderTraverse(T->rchild); 8 }
后序
后序:1.访问左子树
2.访问右子树
3.访问根
总结三个字:左右中


1 /*后序遍历*/ 2 void PostOrderTraverse(BiTree T){ 3 if(T ==NULL) 4 return; 5 PostOrderTraverse(T->lchild); 6 PostOrderTraverse(T->rchild); 7 printf("%c ",T->data); 8 }
对二叉树进行一些其他的操作
销毁二叉树

1 /* 初始条件: 二叉树T存在。操作结果: 销毁二叉树T */ 2 void DestroyBiTree(BiTree *T){ 3 if(*T){ 4 if((*T)->lchild){ //有左孩子 5 DestroyBiTree(&(*T)->lchild); //销毁左孩子子树 6 } 7 if((*T)->rchild){ 8 DestroyBiTree(&(*T)->rchild); 9 } 10 free(*T); /* 释放根结点 */ 11 *T = NULL; //指向0 12 } 13 }
判断是否为空树

1 /*判断是否为空二叉树*/ 2 int BiTreeEmpty(BiTree T){ 3 if(T){ 4 return 0; 5 } 6 return 1; 7 }
求树的深度

1 /* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */ 2 int BiTreeDepth(BiTree T){ 3 int i,j; 4 //没有根节点 5 if(!T){ 6 return 0; 7 } 8 if(T->lchild){ 9 i = BiTreeDepth(T->lchild); 10 }else{ 11 j=0; 12 } 13 if (T->rchild){ 14 j = BiTreeDepth(T->rchild); 15 }else{ 16 i=0; 17 } 18 return i>j ?i+1:j+1; 19 }
全部代码实现

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 5 typedef struct BiNode{ 6 int data; 7 BiNode *lchild,*rchild; 8 9 }BiNode; 10 typedef struct BiNode* BiTree; 11 12 /*初始化并建立二叉树*/ 13 int index=0; 14 void CreateBiTree(BiTree* T,char data[]){ 15 *T =NULL; //初始化为空 16 char ch; 17 if(index<strlen(data)){ 18 ch = data[index++]; 19 }else{ 20 return; 21 } 22 if(ch =='#') //此节点为空 23 *T =NULL; 24 else{ 25 *T = (BiTree)malloc(sizeof(BiNode)); 26 if(!*T) 27 exit(0); 28 (*T)->data=ch; //生成根节点 29 CreateBiTree(&(*T)->lchild,data); 30 CreateBiTree(&(*T)->rchild,data); 31 } 32 } 33 34 /*判断是否为空二叉树*/ 35 int BiTreeEmpty(BiTree T){ 36 if(T){ 37 return 0; 38 } 39 return 1; 40 } 41 42 /* 初始条件: 二叉树T存在。操作结果: 返回T的根 */ 43 char Root(BiTree T){ 44 if(BiTreeEmpty(T)) 45 return NULL; 46 else 47 return T->data; 48 } 49 50 /* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */ 51 int BiTreeDepth(BiTree T){ 52 int i,j; 53 //没有根节点 54 if(!T){ 55 return 0; 56 } 57 if(T->lchild){ 58 i = BiTreeDepth(T->lchild); 59 }else{ 60 j=0; 61 } 62 if (T->rchild){ 63 j = BiTreeDepth(T->rchild); 64 }else{ 65 i=0; 66 } 67 return i>j ?i+1:j+1; 68 } 69 70 /*先序遍历*/ 71 void PreOrderTraverse(BiTree T){ 72 if(T ==NULL) 73 return; 74 printf("%c ",T->data); 75 PreOrderTraverse(T->lchild); 76 PreOrderTraverse(T->rchild); 77 } 78 79 /*中序遍历*/ 80 void InOrderTraverse(BiTree T){ 81 if(T ==NULL) 82 return; 83 InOrderTraverse(T->lchild); 84 printf("%c ",T->data); 85 InOrderTraverse(T->rchild); 86 } 87 /*后序遍历*/ 88 void PostOrderTraverse(BiTree T){ 89 if(T ==NULL) 90 return; 91 PostOrderTraverse(T->lchild); 92 PostOrderTraverse(T->rchild); 93 printf("%c ",T->data); 94 } 95 96 /* 初始条件: 二叉树T存在。操作结果: 销毁二叉树T */ 97 void DestroyBiTree(BiTree *T){ 98 if(*T){ 99 if((*T)->lchild){ //有左孩子 100 DestroyBiTree(&(*T)->lchild); //销毁左孩子子树 101 } 102 if((*T)->rchild){ 103 DestroyBiTree(&(*T)->rchild); 104 } 105 free(*T); /* 释放根结点 */ 106 *T = NULL; //指向0 107 } 108 } 109 110 int main(){ 111 BiTree tree; 112 int i; 113 char data[] = "ABDH#K###E##CFI###G#J##"; 114 //InitBiTree(&tree); 115 CreateBiTree(&tree,data); 116 printf("树是否为空:(1 或 0):%d ",BiTreeEmpty(tree)); 117 printf("树的深度为:%d ",BiTreeDepth(tree)); 118 printf("此时树的头结点为:%c ",Root(tree)); 119 120 printf("先序遍历:"); 121 PreOrderTraverse(tree); 122 printf(" "); 123 124 printf("中序遍历:"); 125 InOrderTraverse(tree); 126 printf(" "); 127 128 printf("后序遍历:"); 129 PostOrderTraverse(tree); 130 printf(" "); 131 132 printf("销毁二叉树 "); 133 DestroyBiTree(&tree); 134 printf("树是否为空:(1 或 0):%d ",BiTreeEmpty(tree)); 135 return 0; 136 }
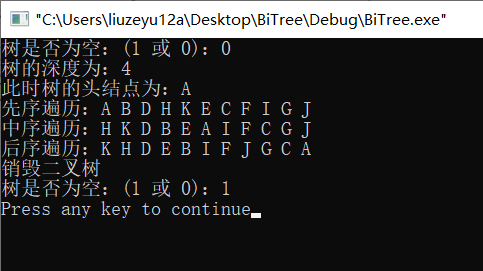
核心要理解的是递归思想,层层调用,并且层层返回,至于函数的调用和堆栈之间的关系,后期在汇编语言里面会解释。
