manacher算法的理解

题目描述

Catcher是MCA国的情报员，他工作时发现敌国会用一些对称的密码进行通信，比如像这些ABBA，ABA，A，123321，但是他们有时会在开始或结束时加入一些无关的字符以防止别国破解。比如进行下列变化 ABBA->12ABBA,ABA->ABAKK,123321->51233214　。因为截获的串太长了，而且存在多种可能的情况（abaaab可看作是aba,或baaab的加密形式），Cathcer的工作量实在是太大了，他只能向电脑高手求助，你能帮Catcher找出最长的有效密码串吗？

解法

题目本质就是求最大回文子串，可以使用manacher算法进行求解。

manache算法图解；如何找到最长子回文；manacher算法总结

我理解的Manacher算法

寻找最长回文子串，我最先想到的是从外向内比对字符串，但看了其他的说法都是中心向外扩散判断是否回文，相对而言，从中心向外扩张会更好（也是manacher算法的关键），但不管哪一个时间复杂度都是o(n²)。而manacher算法可以在o(n)时间内找到最大回文字符串。

要想在o(n)时间内找到最大回文字符串，那么必须要有效的利用已知的信息，这也是manacher算法的关键。思考下面这种情况，当我们访问字符串中以第i个字符为中心的回文时，如何有效利用前面遍历过的字符呢？Manacher算法的解答就是利用回文的特性--对称，来利用先前遍历过的信息。

假设我们正在访问第i个字符，我们需要找出以第i字符为中心的回文，如果此时的字符i正好在之前访问过的某个回文里边，那么我们就可以利用回文对称的特性，找到与位置i相对应的字符，因为这个字符已经访问过了，我们可以直接知道字符i的回文。当已知的回文中心为j那么，字符i对称的位置为k=2*j-i。

  

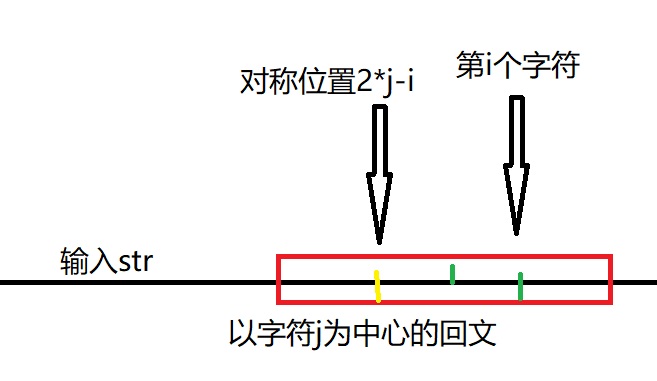
当字符k为中心的回文完全落在字符j的回文中时，此时，字符i的回文长度就等于对称位置的字符长度。

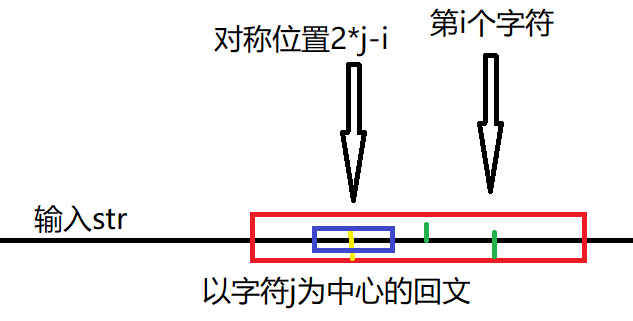
当字符k的回文有部分字符落在了外边，那么需要对在外边的字符进行判断，看看是不是仍属于回文。

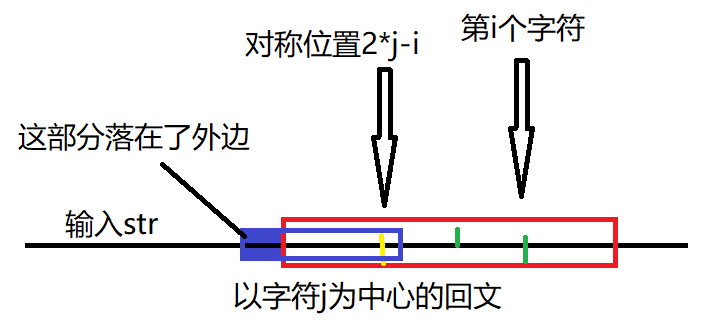
上面是字符i落在某个回文里边的情况，当没有落在某个回文里边时，还是用暴力直接判断以字符i为中心的回文。

题解

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNext()) {
            int maxLen = 0;
            String code = in.next();
            StringBuilder sb = new StringBuilder();
            for (char c : code.toCharArray()) {//处理奇偶回文
                sb.append('#');
                sb.append(c);
            }
            sb.append('#');

            int[] len = new int[sb.length()];//len[i]表示在第i个位置右半径，不包含中心，初始为0
            int center = 0, rb = 0;

            for (int i = 1; i < sb.length()-1; i++) {
                if (i < rb) {
                    len[i] = Math.min(len[2 * center - i], rb - i);//当前字符i包含在最大的回文子串中
                }

                while(i+len[i]+1<sb.length()&&i-len[i]-1>=0&&sb.charAt(i+len[i]+1) == sb.charAt(i-len[i]-1)){//进行扩增
                    len[i] ++;
                }
                if (len[i] > len[center]) {//更新最大长度
                    center = i;
                    rb = center + len[center];
                    maxLen = len[i];
                }
            }
            System.out.println(maxLen);
        }

    }
}