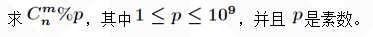组合数取模运算

参考博客：

大数量级组合数的快速计算方法,log转化

 　　组合数取模

　　组合数取模2

组合公式

c(n,m)=p(n,m)/m!=n!/((n-m)!*m!)

c(n,m)=c(n,n-m)

c(n,m)=c(n-1,m)+c(n-1,m-1)

欧拉定理  （<---自家博客）

欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:

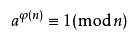
φ(n)表示1~n中与n互质的数的个数

看一个基本的例子。令a = 3，n = 5，这两个数是互素的。比5小的正整数中与5互素的数有1、2、3和4，所以φ(5)=4（详情见[欧拉函数]）。计算:a^{φ(n)} = 3^4 =81，而81= 80 + 1 Ξ 1 （mod 5）

这个定理可以用来简化幂的模运算。比如计算7^{222}的个位数，实际是求7^{222}被10除的余数。7和10[[互素]]，且φ(10)=4。由欧拉定理知7^4Ξ1(mod 10)。所以7^{222}=(7^4)^55*(7^2)Ξ1^{55}*7^2Ξ49Ξ9 (mod 10)。

后话：欧拉定理其实是费马小定理的推广     

 参考：  欧拉-费马小定理定理（证明及推论）

 费马小定理：

　　对于质数p，任意整数a，均满足：a^p≡a（mod p）

 #欧拉定理的推论：

　　若正整数a，n互质，那么对于任意正整数b，有a^b≡a^{b mod φ（n）}（mod n）

ps: 这个推论可以帮助我们在求幂运算的时候缩小数据范围和计算次数。具体的说：在求乘方运算时，可以先把底数对mod取模，再把指数对b mod φ（n）取模。

　　特别的，如果a，mod不互质，且b>φ（n）时，a^b≡a^{b mod φ（n）+ φ（n）}（mod n）

乘法逆元 (目前不会)

介绍：如果ax≡1 (mod p),且gcd(a,p)=1（a与p互质），则称a关于模p的乘法逆元为x。

(a/b) mod p=(a*b^(p-2)) mod p  

条件：p是素数，gcd(b,p)=1，a%b=0

定义： 满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元。

 (PS：p一定是个素数才能对a有乘法逆元（除1），特别注意：当p是1时，对于任意a，k都为1） 

为什么要有乘法逆元呢？ 

当我们要求（a/b） mod p的值（a/b一定是个整数），且a很大，无法直接求得a/b的值时，我们就要用到乘法逆元。 

我们可以通过求b关于p的乘法逆元k，将a乘上k再模p，即(a*k) mod p。 

其结果与(a/b) mod p等价。 

接下来进入正题： 

Lucas定理针对该取值范围较大又不太大的情况 （Lucas定理是用来求 c(n,m) mod p，p为素数的值。）
定理描述 

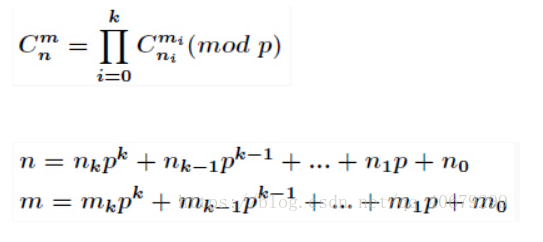
这样将组合数的求解分解为小问题的乘积，下面考虑计算C(ni, mi) %p.

　已知C(n, m) mod p = n!/(m!(n - m)!) mod p。当我们要求（a/b）mod p的值，且b很大，无法直接求得a/b的值时，我们可以转而使用乘法逆元k，将a乘上k再模p，即(a*k) mod p。 其结果与(a/b) mod p等价。

ACM数论之旅10---大组合数-卢卡斯定理（在下卢卡斯，你是我的Master吗？(。-`ω´-) ）

卢卡斯说：

C(n, m) % p  =  C(n / p, m / p) * C(n%p, m%p) % p

对于C(n / p, m / p)，如果n / p 还是很大，可以递归下去，一直到世界的尽头

上代码：

ll Lucas(ll n, ll m, ll p){
    return m ? Lucas(n/p, m/p, p) * C(n%p, m%p, p) % p : 1;
}

....................算了直接给模板吧（Lucas组合数取模运算函数）

ll fact(ll n, ll p){//n的阶乘求余p 
    ll ret = 1;
     for (ll i = 1; i <= n ; i ++) ret = ret * i % p ;
    return ret ;
}
void ex_gcd(ll a, ll b, ll &x, ll &y, ll &d){
    if (!b) {d = a, x = 1, y = 0;}
    else{
        ex_gcd(b, a % b, y, x, d);
        y -= x * (a / b);
    }
}
ll inv(ll t, ll p){//如果不存在，返回-1 //求逆元 
    ll d, x, y;
    ex_gcd(t, p, x, y, d);
    return d == 1 ? (x % p + p) % p : -1;
}
ll comb(ll n, ll m, ll p){//C(n, m) % p
    if (m < 0 || m > n) return 0;
    return fact(n, p) * inv(fact(m, p), p) % p * inv(fact(n-m, p), p) % p;
}

ll Lucas(ll n, ll m, ll p){//Lucas定理求C(n, m) % p 
    return m ? Lucas(n/p, m/p, p) * comb(n%p, m%p, p) % p : 1;
}

关于拓展卢卡斯，也就是卢卡斯的升级版，卢卡斯限定只能取余一个素数，而拓展卢卡斯则没有限定 

其求解方法如下：

　　若不是素数，将p分解质因数，将C(n,m)分别按照Lucas定理中的方法求对p的质因数的模，然后用中国剩余定理合并。

 上模板：

ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(!b){x=1;y=0;return a;}
    ll res=exgcd(b,a%b,x,y),t;
    t=x;x=y;y=t-a/b*y;
    return res;
}

inline ll power(ll a,ll b,ll mod)
{
    ll sm;
    for(sm=1;b;b>>=1,a=a*a%mod)if(b&1)
        sm=sm*a%mod;
    return sm;
}

ll fac(ll n,ll pi,ll pk)
{
    if(!n)return 1;
    ll res=1;
    for(register ll i=2;i<=pk;++i)
        if(i%pi)(res*=i)%=pk;
    res=power(res,n/pk,pk);
    for(register ll i=2;i<=n%pk;++i)
        if(i%pi)(res*=i)%=pk;
    return res*fac(n/pi,pi,pk)%pk;
}

inline ll inv(ll n,ll mod)
{
    ll x,y;
    exgcd(n,mod,x,y);
    return (x+=mod)>mod?x-mod:x;
}

inline ll CRT(ll b,ll mod,ll p){return b*inv(p/mod,mod)%p*(p/mod)%p;}

const int MAXN=11;

static ll w[MAXN];

inline ll C(ll n,ll m,ll pi,ll pk)
{
    ll up=fac(n,pi,pk),d1=fac(m,pi,pk),d2=fac(n-m,pi,pk);
    ll k=0;
    for(register ll i=n;i;i/=pi)k+=i/pi;
    for(register ll i=m;i;i/=pi)k-=i/pi;
    for(register ll i=n-m;i;i/=pi)k-=i/pi;
    return up*inv(d1,pk)%pk*inv(d2,pk)%pk*power(pi,k,pk)%pk;
}

inline ll exlucus(ll n,ll m,ll p)//求C(n, m) % p 
{
    ll res=0,tmp=p,pk;
    static int lim=sqrt(p)+5;
    for(register int i=2;i<=lim;++i)if(tmp%i==0)
    {
        pk=1;while(tmp%i==0)pk*=i,tmp/=i;
        (res+=CRT(C(n,m,i,pk),pk,p))%=p;
    }
    if(tmp>1)(res+=CRT(C(n,m,tmp,tmp),tmp,p))%=p;
    return res;
}

附加：快速乘（如果直接乘会爆ll）

ll mul(ll a, ll b, ll p){//快速乘，计算a*b%p 
    ll ret = 0;
    while(b){
        if(b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

　

实战一下吧

hdu 5446

http://acm.hdu.edu.cn/showproblem.php?pid=5446

题意：

给你三个数n, m, k

第二行是k个数，p1,p2,p3...pk

所有p的值不相同且p都是质数

求C(n, m) % (p1*p2*p3*...*pk)的值

范围：1≤m≤n≤1e18，1≤k≤10，pi≤1e5，保证p1*p2*p3*...*pk≤1e18

AC代码：

#include<cstdio>
typedef long long LL;
const int N = 100000 + 5;
LL mul(LL a, LL b, LL p){//快速乘，计算a*b%p 
    LL ret = 0;
    while(b){
        if(b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}
LL fact(int n, LL p){//n的阶乘求余p 
    LL ret = 1;
     for (int i = 1; i <= n ; i ++) ret = ret * i % p ;
    return ret ;
}
void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
    if (!b) {d = a, x = 1, y = 0;}
    else{
        ex_gcd(b, a % b, y, x, d);
        y -= x * (a / b);
    }
}
LL inv(LL t, LL p){//如果不存在，返回-1 
    LL d, x, y;
    ex_gcd(t, p, x, y, d);
    return d == 1 ? (x % p + p) % p : -1;
}
LL comb(int n, int m, LL p){//C(n, m) % p
    if (m < 0 || m > n) return 0;
    return fact(n, p) * inv(fact(m, p), p) % p * inv(fact(n-m, p), p) % p;
}
LL Lucas(LL n, LL m, int p){
        return m ? Lucas(n/p, m/p, p) * comb(n%p, m%p, p) % p : 1;
}
LL china(int n, LL *a, LL *m){//中国剩余定理 
    LL M = 1, ret = 0;
    for(int i = 0; i < n; i ++) M *= m[i];
    for(int i = 0; i < n; i ++){
        LL w = M / m[i];
        //ret = (ret + w * inv(w, m[i]) * a[i]) % M;//这句写了会WA，用下面那句 
        ret = (ret + mul(w * inv(w, m[i]), a[i], M)) % M;
        //因为这里直接乘会爆long long ,所以我用快速乘(unsigned long long也是爆掉，除非用高精度)
    }
    return (ret + M) % M;
}
int main(){
    int T, k;
    LL n, m, p[15], r[15];
    scanf("%d", &T);
    while(T--){
        scanf("%I64d%I64d%d", &n, &m, &k);
        for(int i = 0; i < k; i ++){
            scanf("%I64d", &p[i]);
            r[i] = Lucas(n, m, p[i]);
        }
        printf("%I64d
", china(k, r, p));
    }
}

我们知道题目要求C(n, m) % (p1*p2*p3*...*pk)的值

其实这个就是中国剩余定理最后算出结果后的最后一步求余

那C(n, m)相当于以前我们需要用中国剩余定理求的值

然而C(n, m)太大，我们只好先算出

C(n, m) % p1 = r1

C(n, m) % p2 = r2

C(n, m) % p3 = r3

.

.

.

C(n, m) % pk = rk

用Lucas，这些r1,r2,r3...rk可以算出来

然后又是用中国剩余定理求答案

附上大佬博客->>>>dalao

这是巨佬的ACM数论之旅