OO第一次单元总结
前三次的OO作业的内容总的来说都是围绕着多项式求导,从最简单的x的幂函数的求导逐渐增加难度,最后完成含有三角函数和嵌套因子的多项式求导。但是在这三次的程序编写和debug中,我也出现了大大小小的问题,所以在此,我对于OO前三次作业的完成做一个总结,使自己对于存在的问题能够认识得更加清晰。
第一次作业
(1)总体概括
-
题目要求
简单多项式求导,多项式的每一项中只含常数和x的幂函数。
-
思路
在第一次作业中,多项式的构造比较简单,所以在这个时候为了更加直观、方便,我选择了正则表达式作为主要的工具对于多项式的每一项进行获取(这也为第三次作业遇到的困难埋下了伏笔),具体的正则表达式如下
(第一项符号比较特殊,单独判断)
第一项的正则表达式:
Pattern p0 = Pattern.compile(
"([+-]?[ \t]*)([+-]?)(\d*)([ \t]*[*]?)" +
"([ \t]*x?)" +
"((?:[ \t]*\^[ \t]*[+-]?\d+)?)");
Matcher m0 = p0.matcher(str);
其他各项的正则表达式:
Pattern p1 = Pattern.compile(
"([+-][ \t]*)([+-]?)(\d*)([ \t]*[*]?)" +
"([ \t]*x?)" +
"((?:[ \t]*\^[ \t]*[+-]?\d+)?)");
Matcher m1 = p1.matcher(str);
(以上正则表达式中存在对于空格的判断问题,在bug分析部分将会具体分析)
在分离出每一项之后,开始进行常规的求导获得每一项求导后的系数和幂指数,最后将这些结果存入一个ArrayList中(同时进行合并同类项),最后进行输出。
-
优化
因为这次作业中只包括常数项和x的幂指数项,所以在优化上主要进行了常数项的合并以及幂指数相同的项系数的合并。
(2)基于度量分析程序结构
-
总体结构介绍
由于第一次作业需要完成的实现比较简单,并且在OO学习的开始面向对象的思想还没有建立起来,所以在第一次作业中我主要还是按照计算过程建了四个类,分别进行每一项的提取、求导、计算长度,以及结果的输出。
-
类图
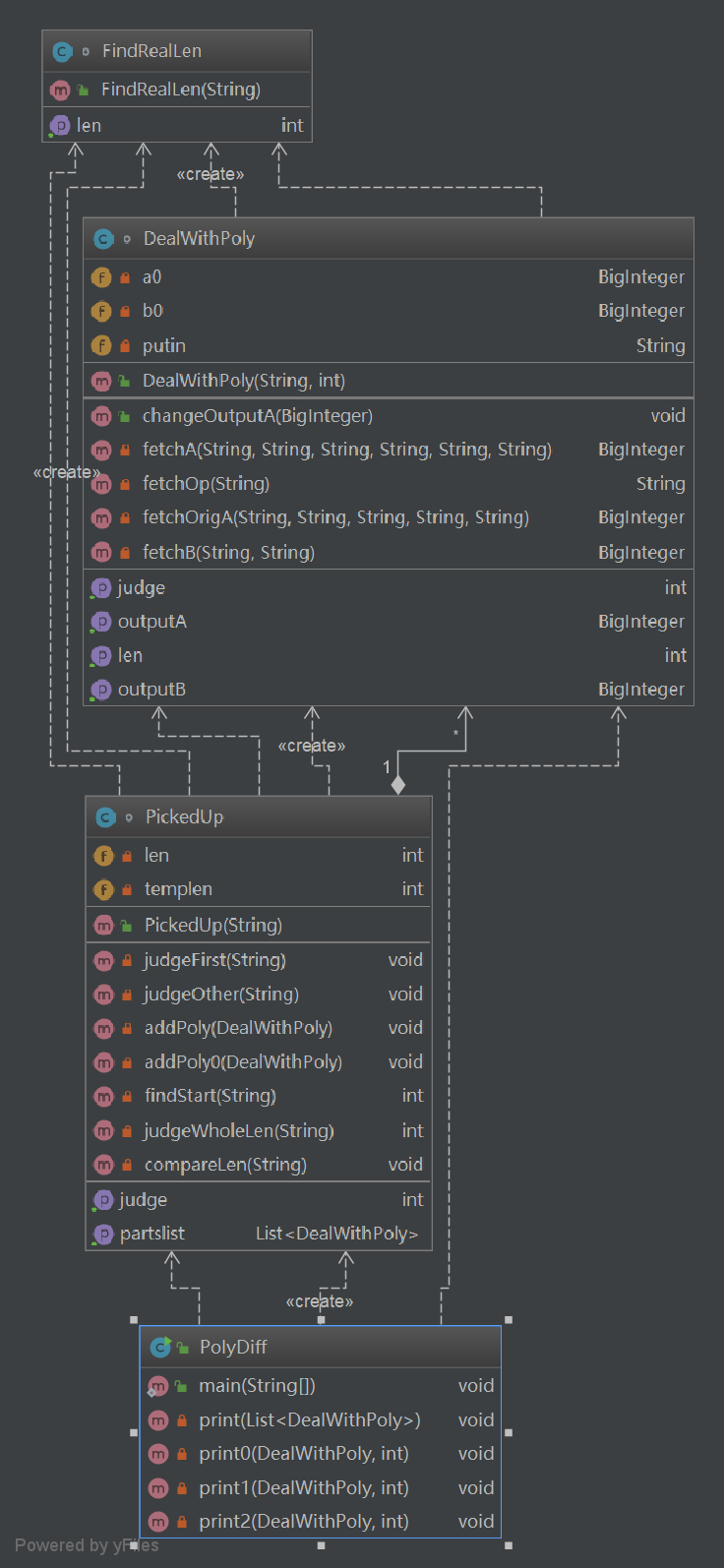
从类图中可以看出,程序主要还是以面向过程的开发为主,并且没有更具体细化每一个类的功能。
-
主要度量图
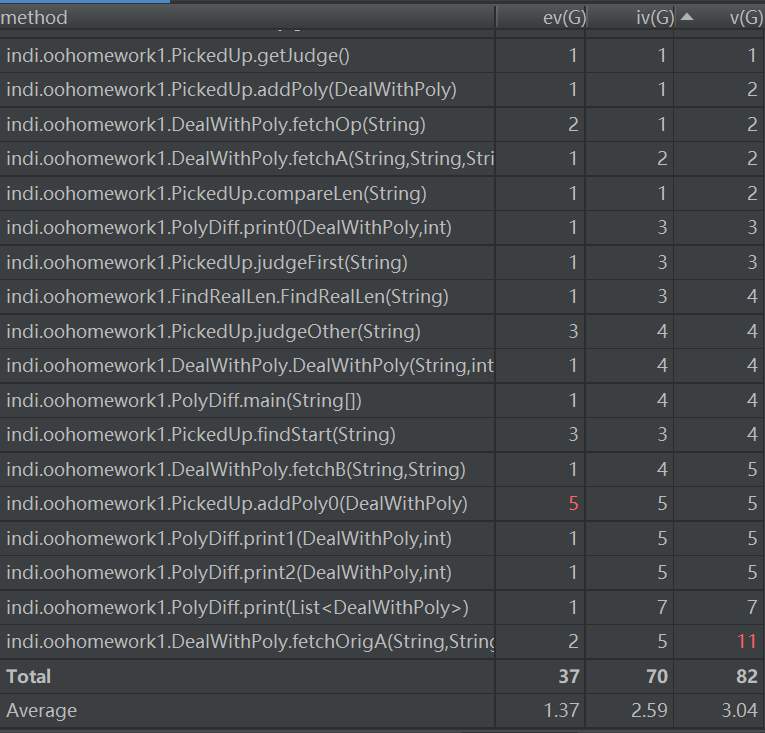

由度量图可以看出,在代码中的一些方法中,ev(G)和v(G)的值过大,说明这些方法的非结构化程度较高、独立路径过多,这也为代码之后的维护带来了困难。除此之外,代码中的类的WMC值普遍偏高,PolyDiff类的Ocavg值也偏高,这也表明着代码的复杂度过高,代码在设计上存在不少不合理的地方。
(3)bug分析
-
自己出现的bug
在第一次作业中,我的程序全部栽在了空格的识别上。
- 没有正确理解指导书的含义,没有在识别空格时将除
<space>和 - 在其中一处正则表达式中忘记加入
\s*.
其实上述的错误都是一些由于理解或粗心而造成的错误,这也充分体现出了我在写代码时对于寻找自己的bug过于忽视,想当然地认为程序已经达到自己的预期效果。需要警醒!!!
- 没有正确理解指导书的含义,没有在识别空格时将除
-
他人的bug——以此为戒
由于第一次的作业比较简单,所以大家的bug都属于比较粗心的错误(比如允许指数中负号与数字间有空格),主要引发这些错误的原因还是因为对于指导书的理解不足。这也体现出了理解题意的重要性,并且在写程序前也应该先预计好可能引发bug的数据从而更好地避开这些致命的小bug。
第二次作业
(1)总体概括
-
题目要求
对于含有常数、x的幂函数、sin(x)的幂函数、cos(x)的幂函数的多项式进行求导。
-
思路
由于第二次作业的因子只有固定、较为规则的四种类型,所以我在最开始读入多项式时将所有的项分为了四个部分,并运用了一个数组存入每个项分别的整个项的系数、x的指数、sin(x)的指数、cos(x)的指数(这也使第三次作业需要重新进行构造)。接着通过求导的公式,对于每一项进行求导,最终得到一个ArrayList并将其输出。
下面是正则表达式的格式(此时已经去掉了表达式中的空格)(由于排版问题,正则表达式的格式可能出现问题):
String teststr1 = "[+-](?:(?:[+-]?[+-]?\d+)|(?: [+-]?" + "(?:(?:sin\(x\))|(?:cos\(x\))|x) (?:\^[+-]?\d+)?))"; String teststr2 = "\*(?:(?:[+-]?\d+)|" + "(?:(?:(?:sin\(x\))|(?:cos\ (x\))|x)(?:\^[+-]?\d+)?))"; String teststr = teststr1 + "(?:" + teststr2 + ")" + "*"; Pattern p = Pattern.compile(teststr); Matcher m = p.matcher(str); -
优化
值得注意的是,这次作业中的sin(x)和cos(x)的格式都非常固定,所以还可以对于(sin(x)^2+cos(x)^2=1)进行化简。在此我的化简策略是在将每一项求导结果加入最终的list的时候就通过查找将符合(sin(x)^2+cos(x)^2=1)的输出项合并,所得新的项在此进行list的插入操作,运用一个递归将最终输出的内容尽可能化为最简。
(2)基于度量分析程序结构
-
总体结构介绍
在本次作业中,我建立了五个类,分别进行输入、输出、提取项、提取因子、对于因子进行求导等操作。但是可以看出,在编程思想上这次作业还是受到了很多面向过程的思想,并且程序的复用性极差。
-
类图
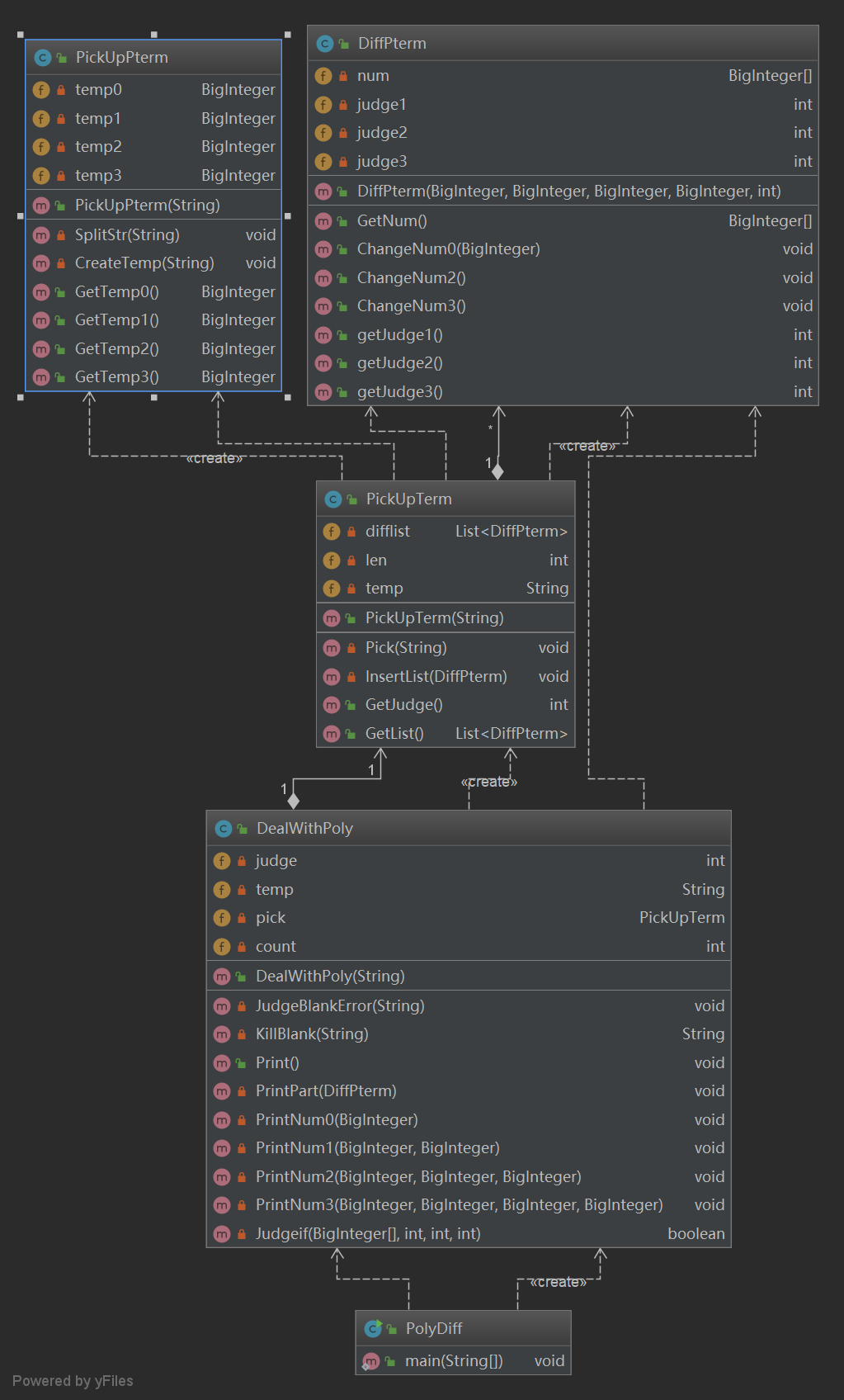
在本次作业中总共建立了5个类,但是每个类的功能还是不够具体,这也导致在下一次作业中无法对于这些类进行沿用。
-
主要度量图
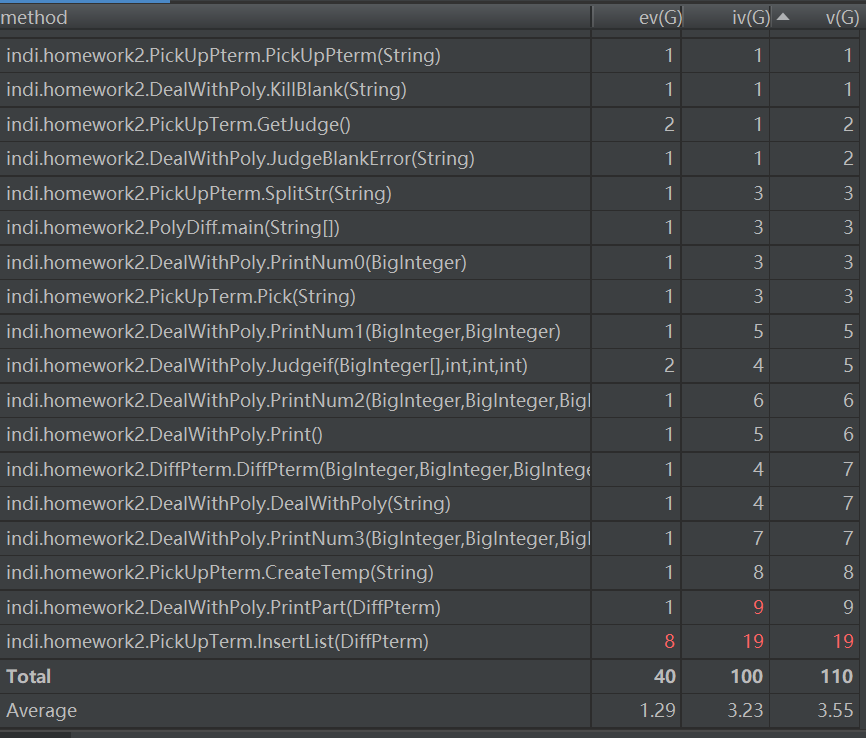

由这次作业的度量图中可以看出方法PrintPart和InsertList的复杂度都过高,这也与其内部带有递归相关。同时对于类的复杂度,可以明显地看到DealWithPoly类的复杂度过高,这也是由于在DealWithPoly类中进行输出时运用过多判断语句,使代码过于冗长。
(3)bug分析
-
自己的bug
在第二次作业中总共出现了两个bug:
- 第一个bug为输出格式错误,错误在输出中换行了,主要为粗心和测试不全面而产生的问题;
- 第二个bug由于沿用了第一次的求导方法而产生的错误:在第一次作业中,由于最终结果不会出现x^-1,所以在输出中我直接将x^-1作为0输出,这种方法在第一次作业的处理中固然简便,然而对于第二次作业却是致命的,因为在第二次作业的结果中会存在x^-1,然而这样的操作却忽视了所有含有x^-1的输出项。
-
他人的bug
这次互测中我发现的他人的bug只要还是格式判断的错误,其原因还是没有对于指导书中的格式要求考虑全面。
第三次作业
(1)总体概括
-
题目要求
这次作业的主要要求仍是进行多项式求导,主要的求导部分仍是常数、x的幂函数、三角函数的幂函数。但是不同之处在于在这次作业中加入了嵌套因子以及表达式因子,表达式的读取方式需变为一种递归处理。
-
思路
刚开始拿到题目时,自己一直在思索应该怎么运用正则表达式来表示出表达式的形式从而判断表达式的格式是否正确,但是苦苦思索无果(java的正则表达式中无法进行递归,且运用正则表达式定会爆栈)。最终,通过理解指导书中推荐方法以及讨论区大佬们对题目的理解,我决定放弃掉在前两次作业中均使用到的长正则表达式,决定使用其他的方式来判断表达式格式是否正确,如判断括号、在局部运用小正则进行特殊格式判断。
判断格式是否错误的正则表达式举例:
Pattern p = Pattern.compile("\*[\+-]+(?:x|s|c)"); Matcher m = p.matcher(str); Pattern p1 = Pattern.compile("\*[\+-]{2,}\d+"); Matcher m1 = p1.matcher(str); Pattern p2 = Pattern.compile("\^[\+-]{2,}\d+"); Matcher m2 = p2.matcher(str); Pattern p3 = Pattern.compile("[\+-]{4,}\d+"); Matcher m3 = p3.matcher(str); Pattern p4 = Pattern.compile("[\+-]{3,}(?:x|s|c)"); Matcher m4 = p4.matcher(str); Pattern p5 = Pattern.compile("sin\([\+-]{2,}\d+"); Matcher m5 = p5.matcher(str); Pattern p6 = Pattern.compile("cos\([\+-]{2,}\d+"); Matcher m6 = p6.matcher(str);在初步判断表达式的格式后,我通过
+和-将表达式分割为项,之后再通过*将每一项分为符合指导书要求的因子。之后再求导操作中,我按照指导书中的因子类型,将需要求导的因子分为常数型、x的幂函数型、多项式因子型、sin(factor)的幂函数型、cos(factor)的幂函数型,并为其建立各自的类,其中由于sin和cos的括号内部可以作为一个因子,所以我们可以再次调用因子求导的类,判断其中的因子是否满足格式要求并进行求导。 -
优化
在第三次作业中,由于我为了方便而在输出的list中没有将每项的系数和幂指数进行分开而是将每一项作为一个系数和字符串的结合体,所以这也使我在想要进行优化时带来了麻烦。但是考虑到本次作业除了常数项能够合并的同类项并不是很多,其实在进行优化时我们只考虑常数项的合并,并将能去掉的括号不进行输出,也能够取得不错的优化效果。
(2)基于度量分析程序结构
-
总体结构介绍
在本次作业中,面向对象的思想终于稍微出现。在作业代码中,总共有10个类,其中除了输入输出、获取因子和项之外,还创设了对于各种因子不同的求导类。
但是,在本次作业中,我忘记使用继承及接口(说到底还是没能理解继承和接口的精髓),导致很多相似的类中的相似代码多次出现,并且没有对于相似的类规定统一的接口。
-
类图
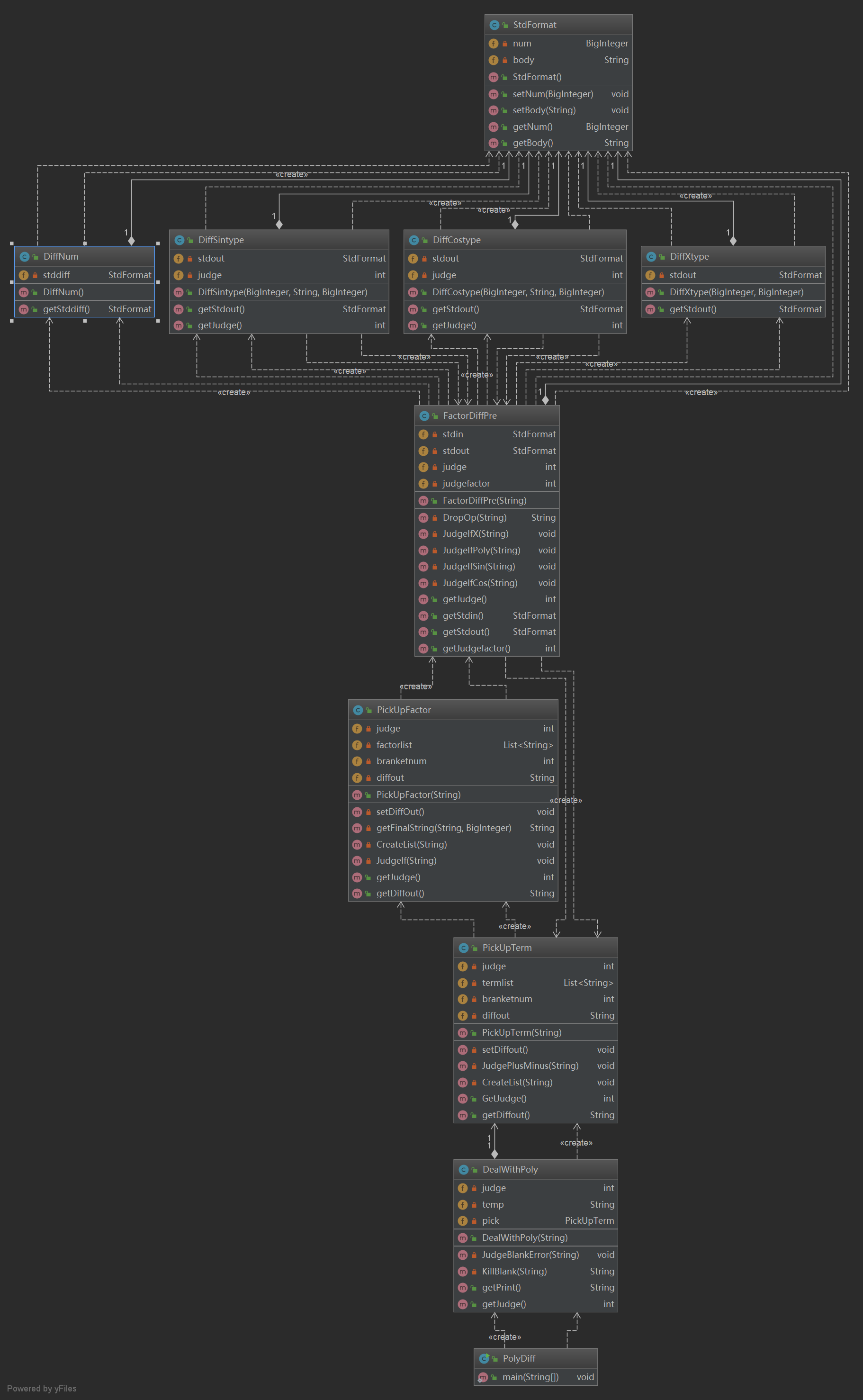
分析类图,可以清晰的看出,在程序中有许多相似的类没能进行程序代码和接口的统一。
-
主要度量图
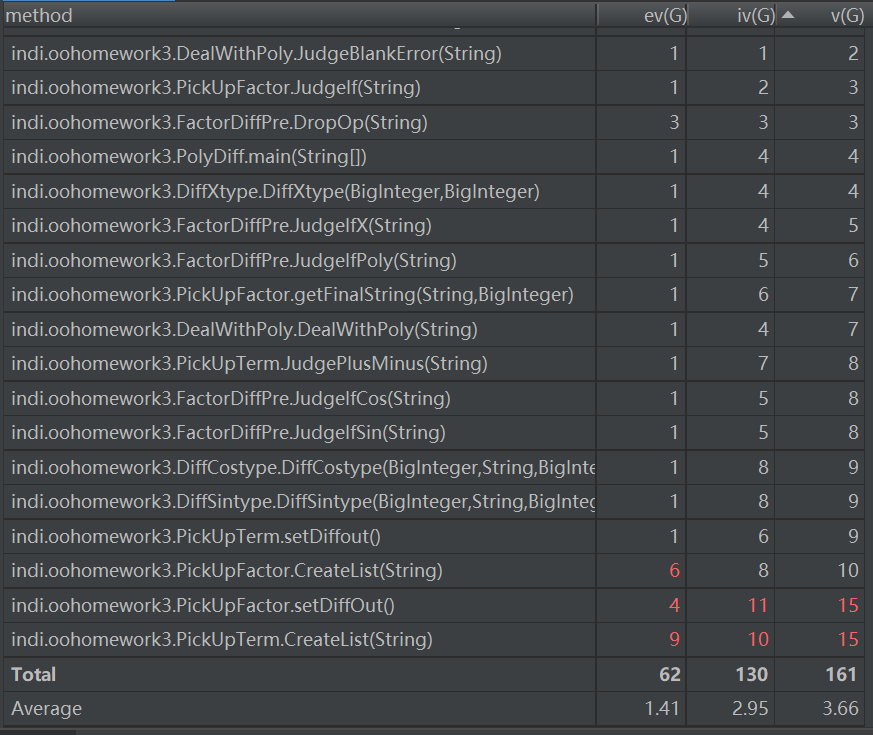

从方法的度量表中可以看出有关求导后结果的list创建的函数中的代码复杂度过高,方法难以进行模块化、难以进行测试和维护,方法的可复用性不高。这也是由于这些方法中的循环和判断语句使用过多造成的。除此之外,PickUpTerm类和PickUpFactor类也过于复杂,对于这些类,复杂度过高的主要原因主要还是运用了面向过程的方法,没有能很好的将它们的功能进行分割。
(3)bug分析
-
自己的bug
在这次作业中,由于在写代码时没有能够保持一个比较清醒的态度,代码也没有很好的模块化,导致有些前面考虑到的情况在后面写相关的代码时忘记了。体现在代码上便是,在进行表达式因子的读取时,没有考虑前面符号(其实在前面的代码中已经对于符号进行了判断)。由于这一行的错误导致强测和互测被刀到肉疼!
这也提醒我在写代码时一定先进行完备的考虑后再进行代码编写,并且在测试时也不能仅仅依靠现有的测试数据,要尽可能寻找可能出现的错误,并将其进行组合。
-
他人的bug
由于这次不允许wf数据的测试,让一些同学逃过了一劫,但是从我找到的错误来看,大家主要还是格式的判断的失误(像我这样由于求导过程的错误实在不多/(ㄒoㄒ)/~~)。主要的错误有:在三角函数中没能正确判断因子格式、在乘法中错误判断格式(主要都出现在常数项的符号判断上)。
(4)寻找他人bug的策略
就着第三次作业我来谈一谈自己在寻找bug时的策略:
- 整体来看,我在前两次作业中的hack策略为“黑盒测试”和“白盒测试”相结合:
- 黑盒测试:主要针对于格式的错误,比如wf的误判等。但是由于在前两次作业中格式的要求比较简单,所以这种测试的效率其实也不算很高,主要在于是否能构造出比
诡异奇特、容易考虑不到的测试点。 - 白盒测试:在前两次作业中,代码量还算比较小,所以进行白盒测试还是有一定的可行性的。但是要想真正完成看完每个人的代码还是不现实的。所以在进行白盒测试时,我主要着眼于空格等格式的判断以及正则表达式的构造、还有输出时符号的判断等。
- 在第三次作业中,由于代码量的增加,并且考虑到大家求导的思路有比较相似,求导步骤出错可能性较小,我只进行了对于格式方面的黑盒测试。运用我在写代码是所考虑到的特殊格式对于同组的代码进行测试。结果显示在第三次作业中,大家的错误的确集中在对于wrong format的判断上,黑盒测试在这次hack中效果还是不错的。
虽然目前为止,我通过现有的方法找到了不少bug,但是相比同组大佬还是相差甚远,所以我也需要在今后的debug之路上更进一步,可以对于程序产生随机数据上进行探索(虽然我觉得通过思考构造数据可能找到bug的效率更高)。
Applying Creational Pattern
在本次实验中,由于我们的求导操作通过因子的类型区分为不同的过程,但是总的来说都是在进行求导这一操作,所以我们可以选择使用工厂模式。
工厂模式:工厂模式是一种实例化对象模式,是用工厂方法代替new操作的一种模式。具体操作主要为建立一个工厂类,对实现了同一接口的一些类进行实例的创建。
重构具体方法:
- 首先我们先决定将哪些类放入一个工厂中——对因子求导的类。
- 之后先使这些类继承一个接口。
- 建立一个工厂,并通过判断条件决定在工厂中调用哪一个类。
- 便可创造出我们所需要的类。同时系统的可扩展性也大大提高。
总结
回顾完成这三次作业的过程,可以明显感受到自己在这一阶段的进步----从一个java小白到现在可以较为熟练地运用java的基本语法,并且对于面向对象编程有了初步的了解和实践。但是不可否认,自己目前还是一个小菜鸡,在程序的构造和debug的能力上有着很大的欠缺,编程的思路也经常很不清晰,对java的了解也不深入。
在接下来的学习中,我也需要有所针对,要不仅能学其所用,更能用其所学。