poj1009

题目大意：边缘检测

IONU卫星成像公司，公司记录和储存非常大的图片使用行程编码，你需要编写一个程序读取被压缩的图像，发现图像的边缘，描述如下，并且输出另一个发现的边缘压缩图像。

一个简单的边缘检测算法设置输出像素的值是它最大的差的绝对值与周围像素的，观看下面的图像

 

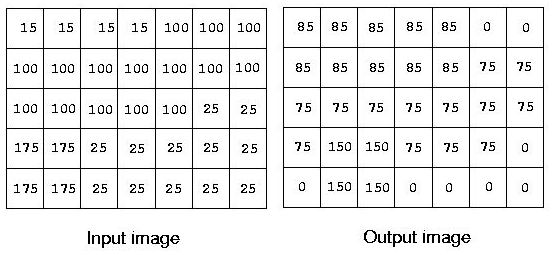
图像包含2-10^9个像素点，所有的像素值都在（0-255）之间，不过为了方便存储，使用相同的数字压缩到一起方式，比如上面图像第一行有4个15可以写成15 4，计算出来最终的图像，也是用压缩的方式写出来

分析：很明显不能够把图像还原，太占内存了，也没有办法计算，再想想吧........

发现可法通过判断上下是否属于同一集合来做，但是首位需要单独考虑，试试吧

8个小时，真心很麻烦啊，不过对了，嘎嘎，好爽

#include<iostream>
#include<queue>
#include<cmath>
#include<algorithm>
#include<string.h>
using namespace std;

#define maxn 1005
#define INF 0xfffffff

int dir[9][2] = {
    {-1,-1},{-1, 0},{-1, 1},
    { 0,-1},{ 0, 0},{ 0, 1},
    { 1,-1},{ 1, 0},{ 1, 1}
};

struct Set
{
    int L, R;
    int vl, cnt;
}a[maxn];

struct node
{
    int vl, cnt;
};

struct SQLine
{
    int Up, Down;
};

int FindSet(int L, int R, int e);           //查找e在第几个区间
int MaxAbs(int k, int wide, int Len, int n);                //与四周相比最大的绝对值
int FindLocation(int L, int R, int wide, int l, int r);   //查找与e相等的最右边的位置
node Fill(int k, int wide, int cnt, int Len, int n);        //填充
int OK(int x, int y, int wide, int Len);    //判断xy坐标是否合法

int main()
{
    int wide;

    while(cin >> wide)
    {
        int n=1;
        node s;
        queue<node> Q;

        if(wide == 0)
        {
            cout << "0" <<endl;
            continue;
        }
        a[0].L = -INF, a[0].R = -1;
        while(cin >> a[n].vl >> a[n].cnt, a[n].vl+a[n].cnt)
        {
            a[n].L = a[n-1].R+1;
            a[n].R = a[n-1].R+a[n].cnt;
            n++;
        }
        a[n].L = a[n-1].R+1, a[n].R=INF;
        int k=0, End = a[n-1].R;
        while(k <= End)
        {
            int indexK = FindSet(0, n, k);

            int Len = FindLocation(k, a[indexK].R, wide, 0, n);

            Q.push(Fill(k++, wide, 1, End/wide+1, n));

            if(Len - k == 0)
                Q.push(Fill(k++, wide, 1, End/wide+1, n));
            else if(Len - k > 0)
            {
                Q.push(Fill(k, wide, Len-k, End/wide+1, n));
                Q.push(Fill(Len, wide, 1, End/wide+1, n));
                k = Len+1;
            }
        }
        s.cnt = s.vl = 0;
        Q.push(s);
        s = Q.front();
        s.cnt = 0;

        cout << wide <<endl;

        while(Q.size())
        {
            node q = Q.front();Q.pop();
            if(s.vl == q.vl)
                s.cnt += q.cnt;

            if(s.vl != q.vl || Q.size() == 0)
            {
                cout<< s.vl << ' ' << s.cnt <<endl;
                s = q;
            }

            if(Q.size() == 0)
                cout << "0 0" <<endl;
        }
    }

    return 0;
}


int FindSet(int L, int R, int e)           //查找e在第几个区间
{
    while(L<=R)
    {
        int Mid = (L+R) / 2;

        if(e >= a[Mid].L && e <= a[Mid].R)
            return Mid;
        else if(e < a[Mid].L)
            R = Mid-1;
        else
            L = Mid+1;
    }

    return 0;
}
int MaxAbs(int k, int wide, int Len, int n)                //与四周相比最大的绝对值
{
    int i, x = k/wide, y=k%wide;
    int MaxNum=0;
    int t = FindSet(0, n, k);

    for(i=0; i<9; i++)
    {
        int nx = x+dir[i][0];
        int ny = y+dir[i][1];

        if(OK(nx, ny, wide, Len))
        {
            int j = nx * wide + ny;
            j = FindSet(0, n, j);
            MaxNum = max(MaxNum, abs(a[t].vl - a[j].vl));
        }
    }

    return MaxNum;
}
int OK(int x, int y, int wide, int Len)   //判断xy坐标是否合法
{
    if(x>=0&&x<Len && y>=0&&y<wide)
        return 1;
    return 0;
}
int FindLocation(int L, int R, int wide, int l, int r)   //查找与e相等的最右边的位置
{
    int Mid, up=FindSet(l, r, L-wide), down=FindSet(l, r, L+wide);
    int ans = L;

    while(L <= R)
    {
        Mid = (L+R) / 2;

        int i=FindSet(l, r, Mid-wide), j=FindSet(l, r, Mid+wide);

        if(up == i && down == j)
            L = Mid+1, ans=Mid;
        else
            R = Mid-1;
    }

    return ans;
}
node Fill(int k, int wide, int cnt, int Len, int n)        //填充
{
    node s;

    s.vl = MaxAbs(k, wide, Len, n);
    s.cnt = cnt;

    return s;

}