常见激活函数的介绍和总结

1、激活函数的概念

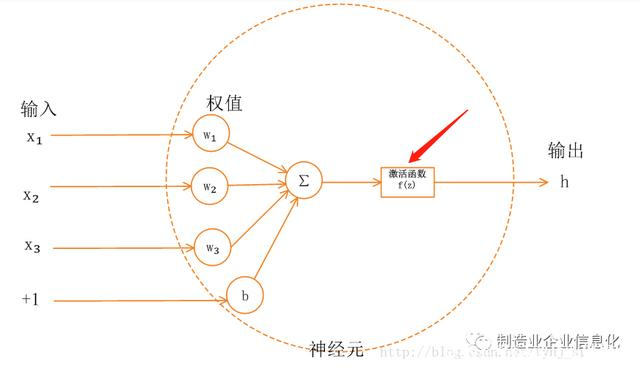
　　神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐层或输出层）。在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数Activation Function（又称激励函数）。

 2、激活函数的本质和作用 

 　　激活函数是来向神经网络中引入非线性因素的，通过激活函数，神经网络就可以拟合各种曲线。如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼*任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

　　为了解释激活函数如何引入非线性因素，接下来让我们以神经网络分割*面空间作为例子。

　　（1）无激活函数的神经网络

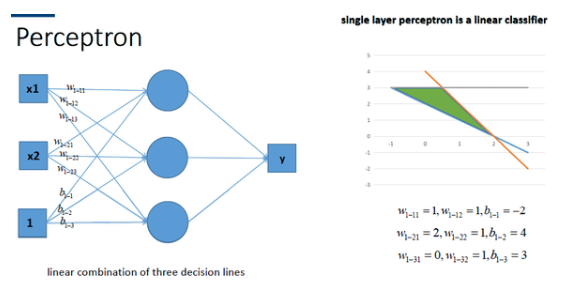
　　神经网络最简单的结构就是单输出的单层感知机，单层感知机只有输入层和输出层，分别代表了神经感受器和神经中枢。下图是一个只有2个输入单元和1个输出单元的简单单层感知机。图中x1、w2代表神经网络的输入神经元受到的刺激，w1、w2代表输入神经元和输出神经元间连接的紧密程度，b代表输出神经元的兴奋阈值，y为输出神经元的输出。我们使用该单层感知机划出一条线将*面分割开，如图所示：

　　同理，我们也可以将多个感知机（注意，不是多层感知机）进行组合获得更强的*面分类能力，如图所示：

 

　　再看看包含一个隐层的多层感知机的情况，如图所示：

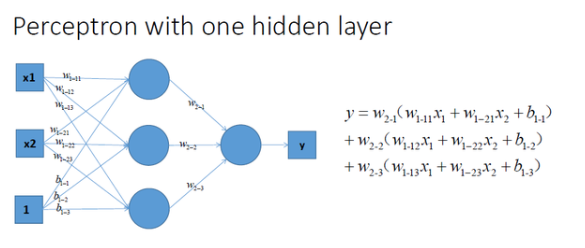
　　通过对比可以发现，上面三种没有激励函数的神经网络的输出是都线性方程，其都是在用复杂的线性组合来试图逼*曲线。

 　　（2）带激活函数的神经网络

　　让我们在神经网络每一层神经元做完线性变换以后，加上一个非线性激励函数对线性变换的结果进行转换，结果显而易见，输出立马变成一个不折不扣的非线性函数了，如图所示： 

 

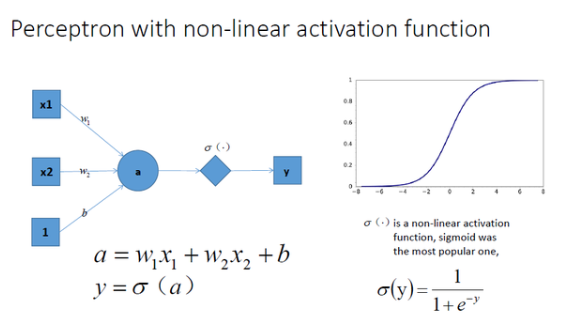
　　拓展到多层神经网络的情况, 和刚刚一样的结构, 加上非线性激励函数之后, 输出就变成了一个复杂的非线性函数了，如图所示： 

 

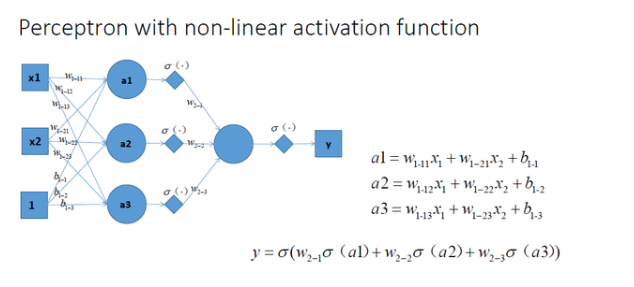
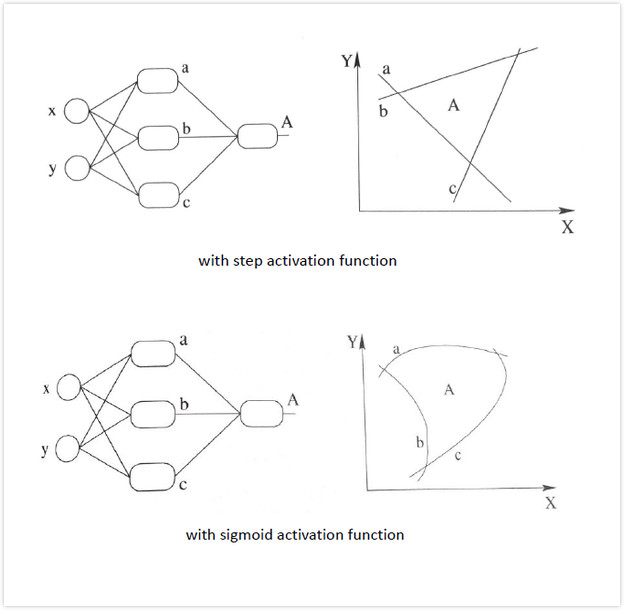
　　总结：加入非线性激励函数后，神经网络就有可能学习到*滑的曲线来分割*面，而不是用复杂的线性组合逼**滑曲线来分割*面，使神经网络的表示能力更强了，能够更好的拟合目标函数。 这就是为什么我们要有非线性的激活函数的原因。如下图所示说明加入非线性激活函数后的差异，上图为用线性组合逼**滑曲线来分割*面，下图为*滑的曲线来分割*面：

 

 3、几种常见的激活函数

　　3.1 sigmoid函数

　　公式： 

 

　　曲线：

 

 

　　Sigmoid函数也叫 Logistic 函数，用于隐层神经元输出，取值范围为(0,1)。它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。

　　Sigmoid函数在历史上曾经非常的常用，输出值范围为[0,1]之间的实数。但是现在它已经不太受欢迎，实际中很少使用。原因是sigmoid存在3个问题：

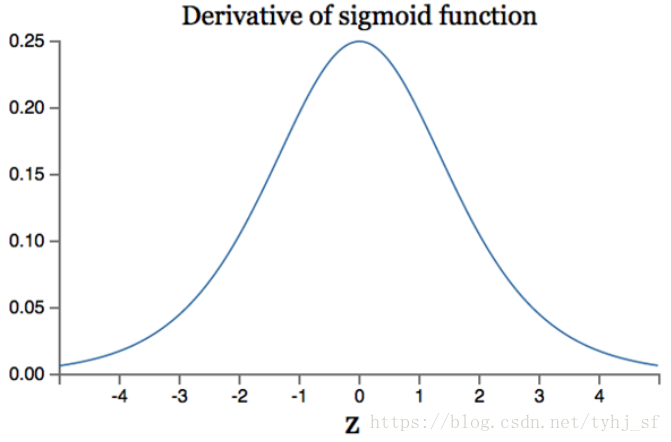
　　1）sigmoid函数饱和使梯度消失(Sigmoidsaturate and kill gradients)。我们从导函数图像中可以看出sigmoid的导数都是小于0.25的，那么在进行反向传播的时候，梯度相乘结果会慢慢的趋*于0。这样，几乎就没有梯度信号通过神经元传递到前面层的梯度更新中，因此这时前面层的权值几乎没有更新，这就叫梯度消失。除此之外，为了防止饱和，必须对于权重矩阵的初始化特别留意。如果初始化权重过大，可能很多神经元得到一个比较小的梯度，致使神经元不能很好的更新权重提前饱和，神经网络就几乎不学习。

　　2）sigmoid函数输出不是“零为中心”(zero-centered)。一个多层的sigmoid神经网络，如果你的输入x都是正数，那么在反向传播中w的梯度传播到网络的某一处时，权值的变化是要么全正要么全负。

　　如上图所示：当梯度从上层传播下来，w的梯度都是用x乘以f的梯度，因此如果神经元输出的梯度是正的，那么所有w的梯度就会是正的，反之亦然。在这个例子中，我们会得到两种权值，权值范围分别位于图8中一三象限。当输入一个值时，w的梯度要么都是正的要么都是负的，当我们想要输入一三象限区域以外的点时，我们将会得到这种并不理想的曲折路线（zig zag path），图中红色曲折路线。假设最优化的一个w矩阵是在图8中的第四象限，那么要将w优化到最优状态，就必须走“之字形”路线，因为你的w要么只能往下走(负数)，要么只能往右走(正的)。优化的时候效率十分低下，模型拟合的过程就会十分缓慢。　　　        3）指数函数的计算是比较消耗计算资源的。其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。

　　3.2 Tanh函数

　　tanh函数跟sigmoid还是很像的，实际上，tanh是sigmoid的变形,如公式5所示。tanh的具体公式如下：

$f(x)=tanh(x)\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$ 

$tanh(x)=2sigmoid(2x)-1$

Tanh函数及其导数的几何图像如下图：

　tanh读作Hyperbolic Tangent，它解决了Sigmoid函数的不是zero-centered输出问题，tanh是“零为中心”的。因此，实际应用中，tanh会比sigmoid更好一些。但是在饱和神经元的情况下，tanh还是没有解决梯度消失问题。

 　　优点：tanh解决了sigmoid的输出非“零为中心”的问题

 　　缺点：（1）依然有sigmoid函数过饱和的问题。（2)依然进行的是指数运算。 

　　3.3 ReLU

 　　*年来，ReLU函数变得越来越受欢迎。全称是Rectified Linear Unit，中文名字：修正线性单元。ReLU是Krizhevsky、Hinton等人在2012年《ImageNet Classification with Deep Convolutional Neural Networks》论文中提出的一种线性且不饱和的激活函数。它的数学表达式如7所示

　　函数图像如下图所示：

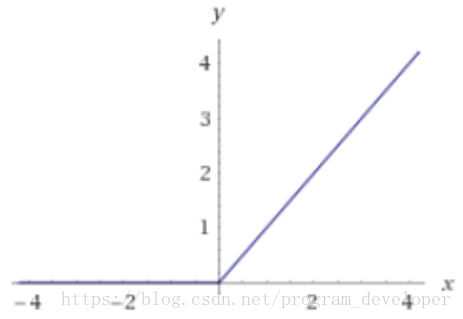
 　　优点：（1）ReLU解决了梯度消失的问题，至少x在正区间内，神经元不会饱和；（2）由于ReLU线性、非饱和的形式，在SGD中能够快速收敛；（3）算速度要快很多。ReLU函数只有线性关系，不需要指数计算，不管在前向传播还是反向传播，计算速度都比sigmoid和tanh快。

　　 缺点：（1）ReLU的输出不是“零为中心”(Notzero-centered output)。（2）随着训练的进行，可能会出现神经元死亡，权重无法更新的情况。这种神经元的死亡是不可逆转的死亡。

 　　总结：训练神经网络的时候，一旦学习率没有设置好，第一次更新权重的时候，输入是负值，那么这个含有ReLU的神经节点就会死亡，再也不会被激活。因为：ReLU的导数在x>0的时候是1，在x<=0的时候是0。如果x<=0，那么ReLU的输出是0，那么反向传播中梯度也是0，权重就不会被更新，导致神经元不再学习。也就是说，这个ReLU激活函数在训练中将不可逆转的死亡，导致了训练数据多样化的丢失。在实际训练中，如果学习率设置的太高，可能会发现网络中40%的神经元都会死掉，且在整个训练集中这些神经元都不会被激活。所以，设置一个合适的较小的学习率，会降低这种情况的发生。所以必须设置一个合理的学习率。为了解决神经元节点死亡的情况，有人提出了Leaky ReLU、P-ReLu、R-ReLU、ELU等激活函数。

　　引出的问题：神经网络中ReLU是线性还是非线性函数？为什么relu这种“看似线性”（分段线性）的激活函数所形成的网络，居然能够增加非线性的表达能力？

　　（1）relu是非线性激活函数。

　　（2）让我们先明白什么是线性网络?如果把线性网络看成一个大的矩阵M。那么输入样本A和B，则会经过同样的线性变换MA，MB（这里A和B经历的线性变换矩阵M是一样的）

　　（3）的确对于单一的样本A，经过由relu激活函数所构成神经网络，其过程确实可以等价是经过了一个线性变换M1，但是对于样本B，在经过同样的网络时，由于每个神经元是否激活（0或者Wx+b）与样本A经过时情形不同了（不同样本），因此B所经历的线性变换M2并不等于M1。因此，relu构成的神经网络虽然对每个样本都是线性变换，但是不同样本之间经历的线性变换M并不一样，所以整个样本空间在经过relu构成的网络时其实是经历了非线性变换的。 

　　3.3.1 Leaky ReLU

　　ReLU是将所有的负值设置为0，造成神经元节点死亡情况。相反，Leaky ReLU是给所有负值赋予一个非零的斜率。Leaky ReLU激活函数是在声学模型(2013)中首次提出来的。它的数学表达式如公式8所示：

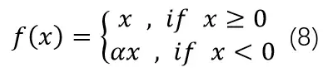
 　　其图像如下图：

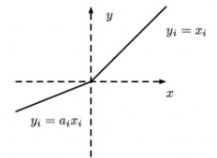
　　优点：

　　（1）神经元不会出现死亡的情况。

　　（2）对于所有的输入，不管是大于等于0还是小于0，神经元不会饱和。

　　（3）由于Leaky ReLU线性、非饱和的形式，在SGD中能够快速收敛。

　　（4）计算速度要快很多。Leaky ReLU函数只有线性关系，不需要指数计算，不管在前向传播还是反向传播，计算速度都比sigmoid和tanh快。

　　缺点：（1）.Leaky ReLU函数中的α，需要通过先验知识人工赋值。

　　总结：Leaky ReLU很好的解决了“dead ReLU”的问题。因为Leaky ReLU保留了x小于0时的梯度，在x小于0时，不会出现神经元死亡的问题。对于Leaky ReLU给出了一个很小的负数梯度值α，这个值是很小的常数。比如：0.01。这样即修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失。但是这个α通常是通过先验知识人工赋值的。 

　　3.3.2  RReLU

　　RReLU的英文全称是“Randomized Leaky ReLU”，中文名字叫“随机修正线性单元”。RReLU是Leaky ReLU的随机版本。它首次是在Kaggle的NDSB比赛中被提出来的,其图像和表达式如下图所示：

 

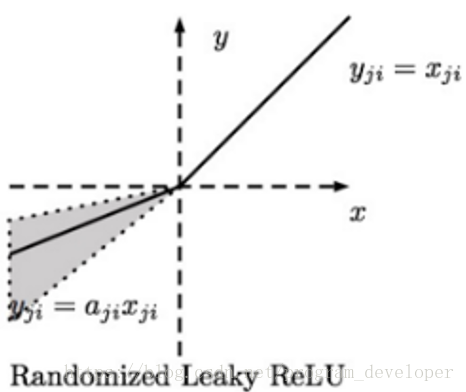
　　RReLU的核心思想是，在训练过程中，α是从一个高斯分布U(l,u)中随机出来的值，然后再在测试过程中进行修正。在测试阶段，把训练过程中所有的a_ji取个*均值。

　　特点：

　　（1）RReLU是Leaky ReLU的random版本，在训练过程中，α是从一个高斯分布中随机出来的，然后再测试过程中进行修正。

　　（2）数学形式与PReLU类似，但RReLU是一种非确定性激活函数，其参数是随机的

 

　　3.3.3  ReLU、Leaky ReLU、PReLU和RReLU的比较

 　　各自图像如下图所示：

 

　　总结：

　　（1）PReLU中的α是根据数据变化的；

　　（2）Leaky ReLU中的α是固定的；

　　（3）RReLU中的α是一个在给定范围内随机抽取的值，这个值在测试环节就会固定下来。 

　　3.4 ELU

　　ELU的英文全称是“Exponential Linear Units”，中文全称是“指数线性单元”。它试图将激活函数的输出*均值接*零，从而加快学习速度。同时，它还能通过正值的标识来避免梯度消失的问题。根据一些研究显示，ELU分类精确度是高于ReLU的。公式如12式所示。

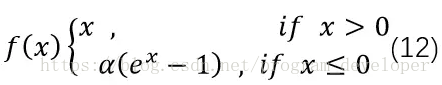
　　ELU与其他几种激活函数的比较图：

 

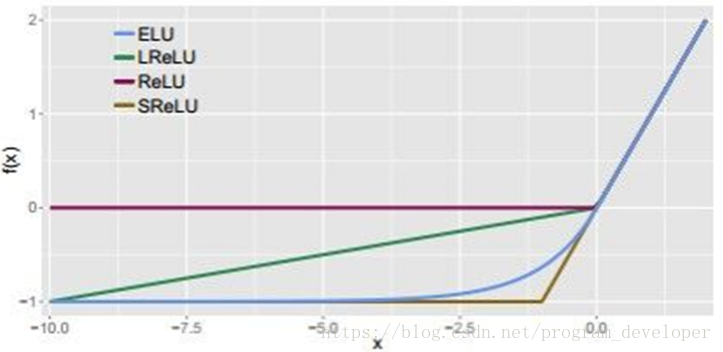
　　优点：

　　（1）ELU包含了ReLU的所有优点。

　　（2）神经元不会出现死亡的情况。

　　（3）ELU激活函数的输出均值是接*于零的。

 　　缺点：

　　（1）计算的时候是需要计算指数的，计算效率低的问题。 

　　3.5 Maxout

　　Maxout “Neuron” 是由Goodfellow等人在2013年提出的一种很有特点的神经元，它的激活函数、计算的变量、计算方式和普通的神经元完全不同，并有两组权重。先得到两个超*面，再进行最大值计算。激活函数是对ReLU和Leaky ReLU的一般化归纳，没有ReLU函数的缺点，不会出现激活函数饱和神经元死亡的情况。Maxout出现在ICML2013上，作者Goodfellow将maxout和dropout结合，称在MNIST，CIFAR-10，CIFAR-100，SVHN这4个数据集上都取得了start-of-art的识别率。Maxout公式如下所示：

$f_{i}(x)=max_{j\epsilon [1,k]}z_{ij}$

　　其中$z_{ij}=x^{T}W_{...ij}+b_{ij}$，假设w是2维的，那么我们可以得出公式如下：

$f(x)=max(w_{1}^{T}x+b_{1},w_{2}^{T}x+b_{2})$

　　分析上式可以注意到，ReLU和Leaky ReLU都是它的一个变形。比如的时候，就是ReLU。Maxout的拟合能力非常强，它可以拟合任意的凸函数。Goodfellow在论文中从数学的角度上也证明了这个结论，只需要2个Maxout节点就可以拟合任意的凸函数，前提是“隐含层”节点的个数足够多。

 　　 优点：

　　（1）Maxout具有ReLU的所有优点，线性、不饱和性。

　　（2）同时没有ReLU的一些缺点。如：神经元的死亡。

　　  缺点：

　　（1）从这个激活函数的公式14中可以看出，每个neuron将有两组w，那么参数就增加了一倍。这就导致了整体参数的数量激增。

　　3.6 softmax函数

　　Softmax - 用于多分类神经网络输出，公式 为：

 　　举个例子来看公式的意思： 

 　　就是如果某一个 zj 大过其他 z, 那这个映射的分量就逼*于 1,其他就逼*于 0，主要应用就是多分类。

　　为什么要取指数，第一个原因是要模拟 max 的行为，所以要让大的更大。第二个原因是需要一个可导的函数。

4、 sigmoid ，ReLU， softmax 的比较

　　Sigmoid 和 ReLU 比较：

　　sigmoid 的梯度消失问题，ReLU 的导数就不存在这样的问题，它的导数表达式如下： 

 　　曲线如图： 

 

　　对比sigmoid类函数主要变化是：
　　1）单侧抑制
　　2）相对宽阔的兴奋边界
　　3）稀疏激活性。

　　Sigmoid 和 Softmax 区别：

　　softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1。sigmoid将一个real value映射到（0,1）的区间，用来做二分类。而 softmax 把一个 k 维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中 bi 是一个 0～1 的常数，输出神经元之和为 1.0，所以相当于概率值，然后可以根据 bi 的概率大小来进行多分类的任务。二分类问题时 sigmoid 和 softmax 是一样的，求的都是 cross entropy loss，而 softmax 可以用于多分类问题

　　softmax是sigmoid的扩展，因为，当类别数 k＝2 时，softmax 回归退化为 logistic 回归。具体地说，当 k＝2 时，softmax 回归的假设函数为： 

 　　利用softmax回归参数冗余的特点，从两个参数向量中都减去向量θ1 ，得到： 

　　 最后，用 θ′ 来表示 θ2−θ1，上述公式可以表示为 softmax 回归器预测其中一个类别的概率为： 

 

另一个类别概率的为： 

 

　　这与 logistic回归是一致的。

　　softmax建模使用的分布是多项式分布，而logistic则基于伯努利分布。多个logistic回归通过叠加也同样可以实现多分类的效果，但是 softmax回归进行的多分类，类与类之间是互斥的，即一个输入只能被归为一类；多个logistic回归进行多分类，输出的类别并不是互斥的，即"苹果"这个词语既属于"水果"类也属于"3C"类别。 

5、如何选择合适的激活函数

　　如何选择合适的激活函数，目前还不存在定论，在实践过程中更多还是需要结合实际情况，考虑不同激活函数的优缺点综合使用。

　　（1）通常来说，不能把各种激活函数串起来在一个网络中使用。

　　（2）如果使用ReLU，那么一定要小心设置学习率(learning rate),并且要注意不要让网络中出现很多死亡神经元。如果死亡神经元过多的问题不好解决，可以试试Leaky ReLU、PReLU、或者Maxout。

　　（3）尽量不要使用sigmoid激活函数，可以试试tanh，不过tanh的效果会比不上ReLU和Maxout。

 

参考：

https://www.cnblogs.com/XDU-Lakers/p/10557496.html

https://baijiahao.baidu.com/s?id=1665988111893224009&wfr=spider&for=pc

https://www.jianshu.com/p/22d9720dbf1a