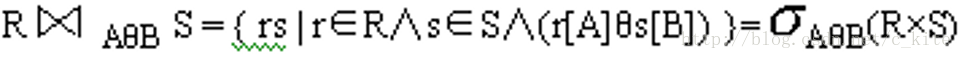关系运算
- 基于代数的定义:关系代数
- 基于逻辑的定义:关系演算
由于使用变量的不同,关系演算又分为元组关系演算和域关系演算。
关系代数
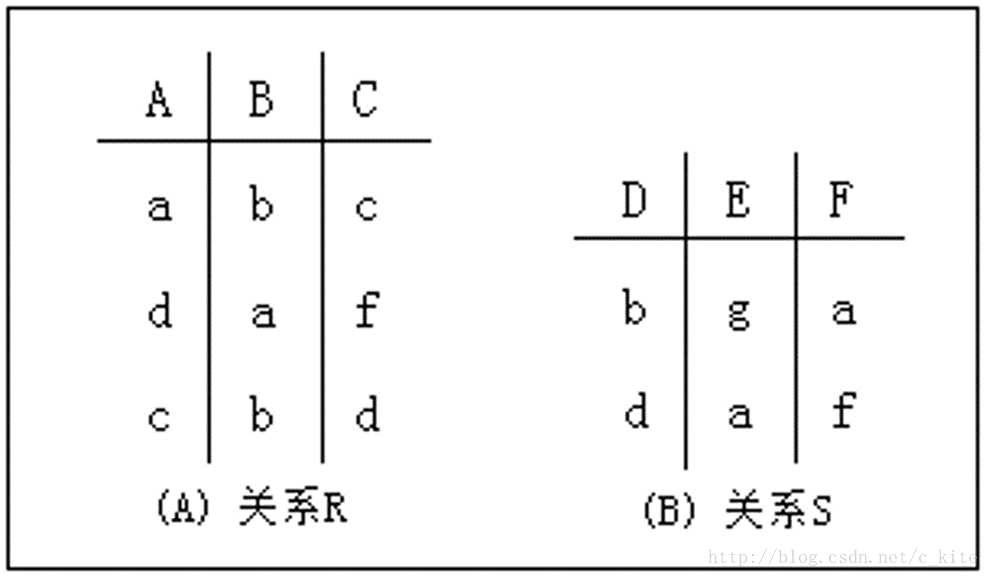
例: 两个关系实例
(1.) 并运算
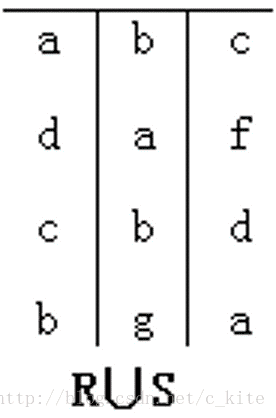
设R和S是n元关系,而且两者各对应属性的数据类型也相同。R和S的并操作定义为 R∪S = { t | t∈R∨t∈S }。
白话: R和S关系合一起, 相同的不写
(2.) 差操作
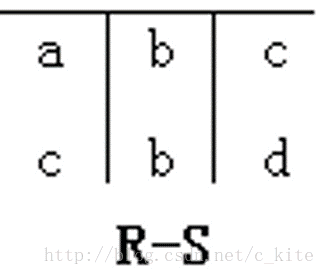
设R和S是n元关系,而且两者各对应属性的数据类型也相同。R和S的差定义为 R-S ={ t | t∈R∧tS}。
白话: 因为是R-S, 找R在S关系中没有的
(3.) 笛卡尔乘积
设R是n元关系,S是m元关系,R和S的的笛卡尔积定义为
R×S={(r1,…,rn,s1,…,sm)|(r1,…, rn )∈R∧(s1, …,sm )∈S}。
白话: 和普通的笛卡尔乘机差不多, 自己看看, 规律很好找.
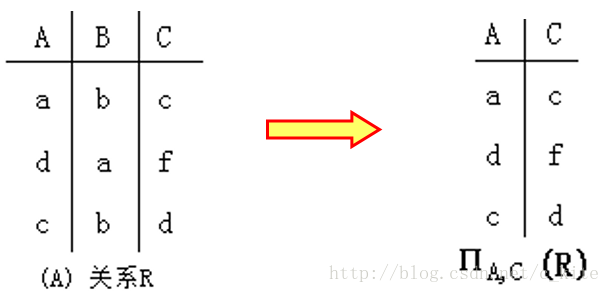
(4. ) 投影操作
设R是一个n元关系,R的投影操作定义为
∏i1,i2,…,im(R) = {(ri1, …,rim)|(r1 ,…,ri1,…,rim,…,rn)∈R}。
白话: 看横行, 如果有两个横行相同, 只写一个. 因此若是S关系投影操作的话, 也就是有b和a
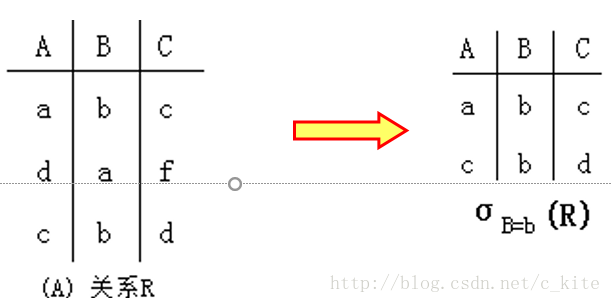
(5. ) 选择操作
设R是一个n元关系,F是一个形如riθc的公式,其中θ∈{=,≠,>,<,≤,≥},R的选择操作定义为F(R)={(r1,…,ri ,…,rn )|(r1,…,ri ,…,rn )∈R∧riθc }。
白话: 把符合条件的拿出来
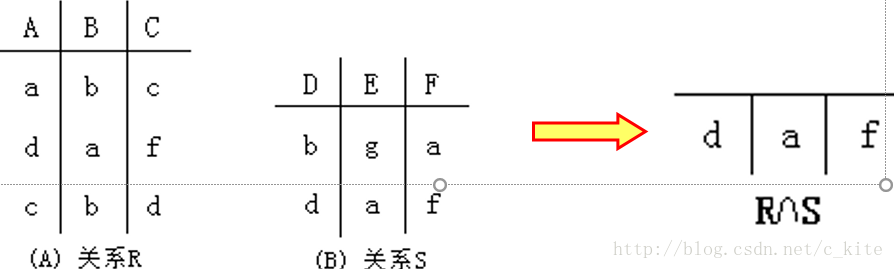
(6. ) 交操作
设R和S是n元关系,而且两者各对应属性的数据类型也相同。R和S的交操作定义为 R S = { t | t∈R∧t∈S }= R-(R-S)。
白话: 相同的拿出来
(7. ) 连接操作
设R是n元关系,S是m元关系,A是R的属性,B是S的属性,A和B的值域具有相同的数据类型,θ∈{=, ≠, >, <, ≤, ≥}。R和S的连接操作定义为
其中,r[A]表示元组r在属性A上的值,s[B]表示元组s在属性B上的值。我们称A和B是连接属性。
白话: 两个关系先做笛卡尔积运算, 然后再根据条件进行比对. 留下符合条件的
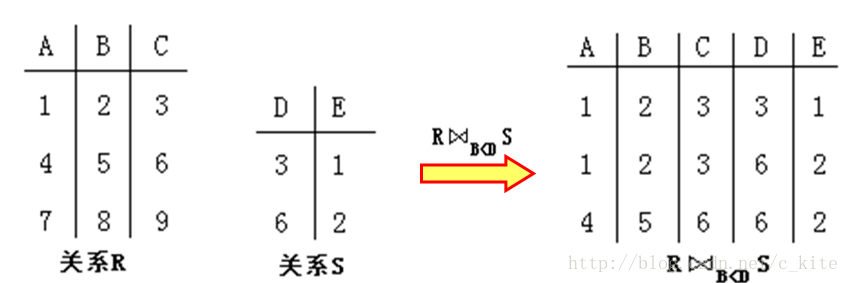
例子:
(7. 1) 几个特殊的连接操作
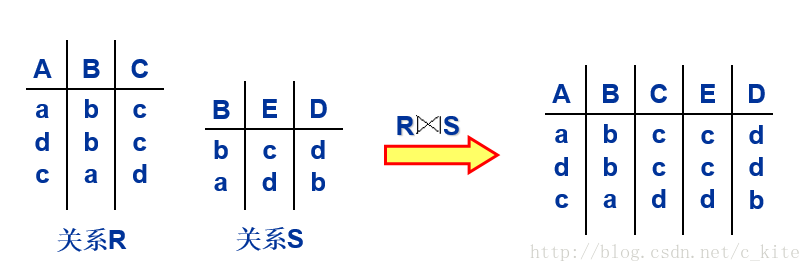
①自然连接 设Att(R)和Att(S)分别是R和S的属性集合。连接条件为R.B=S.B,连接的结果关系的属性集合为Att(R)∪(Att(S)-{B}),即B在结果关系中只出现一次。称这样的连接操作为自然连接操作,
白话: 找相同的然后拼在一起, 例如B属性, 看看下面的例子;
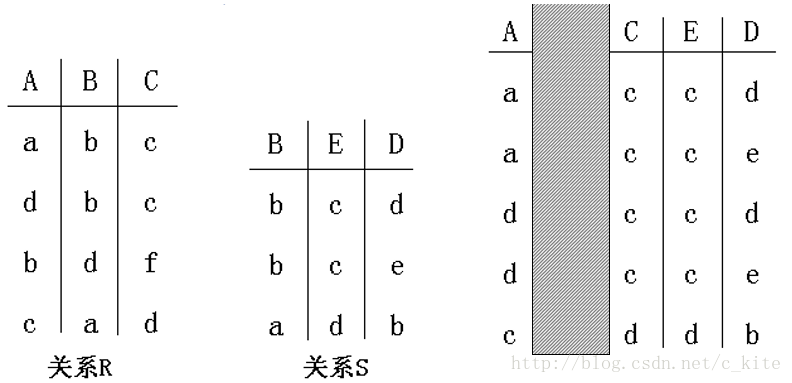
②复合连接 类似于自然连接,只是连接结果不包含连接属性。
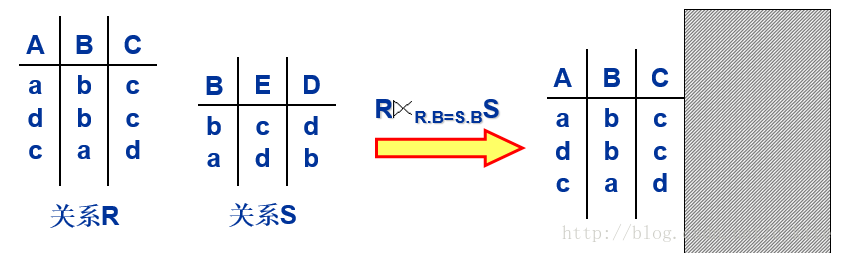
③半连接
白话: 下面的例子由于是R半链接S, 则因此拿R去和S所比较
(8. ) 商操作
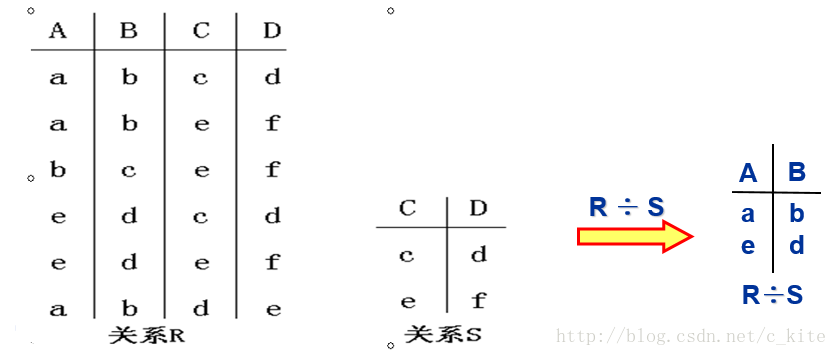
设R和S是两个关系,Z是R的属性集合,X是S的属性集合,XZ,Y=Z-X。R除以S的商定义为R÷S={t|t∏Y(R)且sS, tsR},其中,ts表示由t和s的各属性值构成的一个R关系元组。
白话: 看下面的例子, 因为C, D是关系S中的两个属性, 因此在R集合对除了C, D的属性, 即A, B两属性进行投影, 得到a, b; b, c; e, d;这三组, 然后用这个结果与关系S进行笛卡尔积运算, 发现b c c d这组在关系R中没有, 其余a, b; e, d; 做的运算在R中存在. 因此最后结果为a, b; e, d;