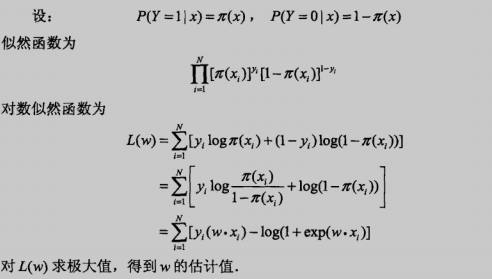一、从最普通的线性模型说起
给定由$d$个属性描述的变量$x=(x_{1};x_{1};...;x_{d};)$,其中$x_{d}$是$x$的第$i$个属性的取值,线性模型(linear model)是试图学习到一个属性的线性组合来进行预测的函数:
$y=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b=w^{T}x+b$
所谓的学习,就是学习其中的$w$和b,学得参数后,模型就得以确定。
但是线性模型并不仅仅满足于去拟合预测值y,也许有可能线性模型可以逼近y的衍生物,意思就是说,$w^{T}x+b$除了可以描述$y$以外,还可以描述$y$的函数,比如$logy$,$y^{2}$等。上面的模型可以叫做多元线性回归。
接下来介绍一种对数线性回归,就是说,预测值可能是随指数增长的,这种情况现实中也很多见,比如传染病的传播,就是指数增长的,当前感染人数越多,就意味着下一阶段感染人数会激增,这种情况就是指数增长。那我们可以用$y=e^{x}$这个简单的指数函数来描述,但是这里没有线性组合啊,于是我们用线性组合去替换x,得到:
$logy=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}$
这里省去了b,这个式子可以叫做对数线性回归,因为它是用线性组合来拟合y的对数形式。
二、逻辑斯蒂回归/对数几率回归
还有一种模型,是用线性组合来拟合y的几率,叫做对数几率回归:
$logfrac{y}{1-y}=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}$
如果我们经过一个简单的变换的话,可以得到:
$y=frac{exp(wx)}{1+exp(wx)}$
$1-y=frac{1}{1+exp(wx)}$
我们发现一个神奇的事情,右式是小于1的数,且和为1,既然我们的线性回归可以用来拟合y值,为什么不把y看做是输出某值的概率呢?所以上式可以做一下替换:
$P(y=1mid x)=frac{exp(wx)}{1+exp(wx)}$
$P(y=0mid x)=frac{1}{1+exp(wx)}$
$logfrac{P(y=1mid x)}{P(y=0mid x)}=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}$
这个模型的参数估计也比较容易,因为我们已经明确的把概率分布给写了出来: