某公司运筹优化岗位第一次面试

P问题， NP问题， NPC问题， NP-hard问题

1. 基本概念

• 复杂度级别: 1)多项式级别O(n^{k);2)非多项式级别，如，指数级O(a}n)和阶乘级别O(n!)。后者的复杂度无论如何都大于前者。
• 归约(约化)：如果能找到这样一个多项式变换法则，对任意一个程序A的输入，都能按这个法则变换为程序B的输入，使两程序的输出相同，那么我们说，问题A可归约为问题B。
  • 通俗解释：一个问题A可以归约为问题B指，可以用问题B的解法解决问题A，或者说，问题A可以“变成”问题B。
  • 特点：“问题A可归约为问题B”有一个直观意义，B的时间复杂度高于或者等于A的时间复杂度，既，问题A不比问题B难。
  • 性质：传递性。如果问题A可以归约为问题B，问题B可以归约为问题C，则问题A一定可以归约为问题C。

2. P问题， NP问题， NPC问题， NP-hard问题的定义和相互关系

• P问题(polynomial)：求解一个问题的时间复杂度是多项式级别
• NP问题(nondeterministic polynomial)：可以在多项式时间里验证解是否正确的问题。定义NP问题的意义在于，如果一个问题不能在多项式时间验证，则这个问题一定没有多项式时间的算法。
  • 图中某条路是否是Hamilton回路，可以在多项式时间验证，是NP问题图中
  • 是否不存在Hamilton回路，不可以在多项式时间验证。
• NPC问题(nondeterministic polynomial complete)：
  • 定义：一个问题1）它是NP问题；2）所有的问题都可以约化到它，这样的问题称为NPC问题。
  • 证明：1）先证明它是NP问题；2）再证明其中一个已知的NPC问题能约化到它（由约化的传递性，如果A能约化到B，则B的时间复杂度不低于A）。
  • 特点：NPC问题目前没有多项式的有效解法，只能有指数级或阶乘级复杂度的算法搜索
• NP-hard问题(nondeterministic polynomial - hard)：满足NPC问题的第2条但是不一定满足第1条。即使NPC问题获得了多项式级别的求解算法，NP-hard问题可能仍然找不到多项式级的算法。
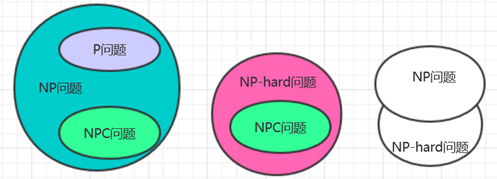
• 他们之间的关系：
  • P问题一定是NP问题，当前无法证明NP问题是否是P问题。但普遍认为P≠NP。于是NP问题包含P问题。
  • NP问题可以归约为NPC问题，所以NP问题包含NPC问题

参考资料：

• 什么是P问题、NP问题和NPC问题
• 最新证明面临质疑：P／NP问题为什么这么难?

动态规划解背包问题

一维背包问题

def dynamicAlgorithm_Knapscak(w, v, b):
    """用动态规划方法求解背包问题
    输入：
        w: 物品的重量 dtype int
        v: 物品的价值 dtype int
        b: 背包的重量
    输出：
        x：最优解，各个物品是否装入背包
        max_value：装入背包的物品的重量
    """
    # 判断异常
    if len(w)!=len(v):
        print('请检查输入')
        return -1,0
    
    # 边界条件
    n = len(w)
    # F[i,j] 当背包重量为j，可取前i个物品时,可装入物品的最大重量
    F = np.zeros((n+1, b+1), dtype=int) 
    # info[i,j],当背包重量为j，可取前i个物品时, 装入的物品的最大标号
    info = np.zeros((n+1, b+1), dtype=int)  
    F[:,0] = 0
    F[0,:] = 0
    
    # 递推 转移方程：F_k(y) = F_k(y-x) + v_k
    for y in range(1,b+1):
        for k in range(1,n+1):
            F[k, y] = F[k-1, y]
            info[k, y] = info[k-1, y]
            if (y-w[k-1] >= 0) & ( F[k-1, y-w[k-1]]+v[k-1] > F[k, y]):
                F[k, y] = F[k-1,y-w[k-1]] + v[k-1]
                info[k, y] = k
                
    # 追踪结果
    x = np.zeros(n, dtype=int)
    max_value = F[-1,-1]
    k = info[-1,-1]
    leftb = b
    while k > 0:
        x[k-1] = 1
        leftb = leftb - w[k-1]
        k = info[k-1, leftb]
    # 输出
    return x, max_value

• 测试用例

v = np.random.randint(1,100,1000,dtype=int)
w = np.random.randint(1,100,1000,dtype=int)
b = int(w.sum()*0.4)
x, max_value = dynamicAlgorithm_Knapscak(w, v, b)
print(x.sum(), max_value)

解二维背包问题

def dynamicAlgorithm_Knapscak(w, v, b):
    """
    w: 物品的重量和体积 多维数组，dtype int
    v: 物品的价值 dtype int
    b: 最大体积和最大重量
    F_k(y) = F_k(y-x) + v_k
    """
    if len(w[0])!=len(v):
        print('请检查输入')
        return -1,0
    
    # 边界条件
    n = len(v)
    F = np.zeros((n+1, b[0]+1, b[1]+1), dtype=int)
    info = np.zeros((n+1, b[0]+1, b[1]+1), dtype=int) # 装入的物品的最大标号
    
    # 递推
    for k in range(1,n+1):
        for y1 in range(1,b[0]+1):
            if (y1-w[0,k-1] >= 0):
                for y2 in range(1,b[1]+1):
                    F[k, y1, y2] = F[k-1, y1, y2]
                    info[k, y1, y2] = info[k-1, y1, y2]
                    if (y2-w[1,k-1] >= 0):
                        if F[k-1, y1-w[0,k-1], y2-w[1,k-1]] + v[k-1] > F[k, y1, y2]:
                            F[k, y1, y2] = F[k-1, y1-w[0,k-1], y2-w[1,k-1]]+v[k-1]
                            info[k, y1, y2] = k
            else:
                F[k, y1, :] = F[k-1, y1, :]
                info[k, y1, :] = info[k-1, y1, :]
            
    # 追踪结果
    x = np.zeros(n, dtype=int)
    max_value = F[-1, -1, -1]
    k = info[-1, -1, -1]
    leftw = b[0]
    leftc = b[1]
    while k > 0:
        x[k-1] = 1
        leftw = leftw - w[0, k-1]
        leftc = leftc - w[1, k-1]
        k = info[k-1, leftw, leftc]
    # 输出
    return x, max_value

• 测试用例

w = np.random.randint(1,60,(2,1000),dtype=int)
b = [120,120]
v = np.random.randint(2,5000,1000,dtype=int)
x, max_value = dynamicAlgorithm_Knapscak(w, v, b)
print('x = :',x, '
 max_value=', max_value)

• 伪多项式变换时间算法近似求解背包问题（屈婉玲： 算法设计与分析p262）
  • 对偶 + 让所有的物品的重量缩小一定倍数，并取整

参考资料：

• 屈婉玲： 算法设计与分析

求一个向量中的第k小的元素

def partition(nums,l,r):
        k = random.randint(l+1,r)
        nums[l], nums[k] = nums[k], nums[l]
        i = l+1    # [l+1, i) <= nums[l]
        j = r    # (j, r] > nums[l]
        while True:
            while (i <= r) and (nums[i] < nums[l]):
                i +=1
            while (j >= l+1) and nums[j] > nums[l]:
                j -=1
            if i > j:
                break
            nums[i], nums[j] = nums[j], nums[i]
            i +=1
            j -=1
        nums[l],nums[j] = nums[j], nums[l]
        return j

def findKthMinest(nums, kth):
    l = 0; r = len(nums)-1
    while True:
        mid = partition(nums, l, r)
        if mid+1 == kth:
            return nums[mid]
        elif mid+1 < kth:
            l = mid+1
            kth = kth-(mid+1)
        else:
            r = mid   

参考资料：

• 215. Kth Largest Element in an Array

整数规划的求解方法总结

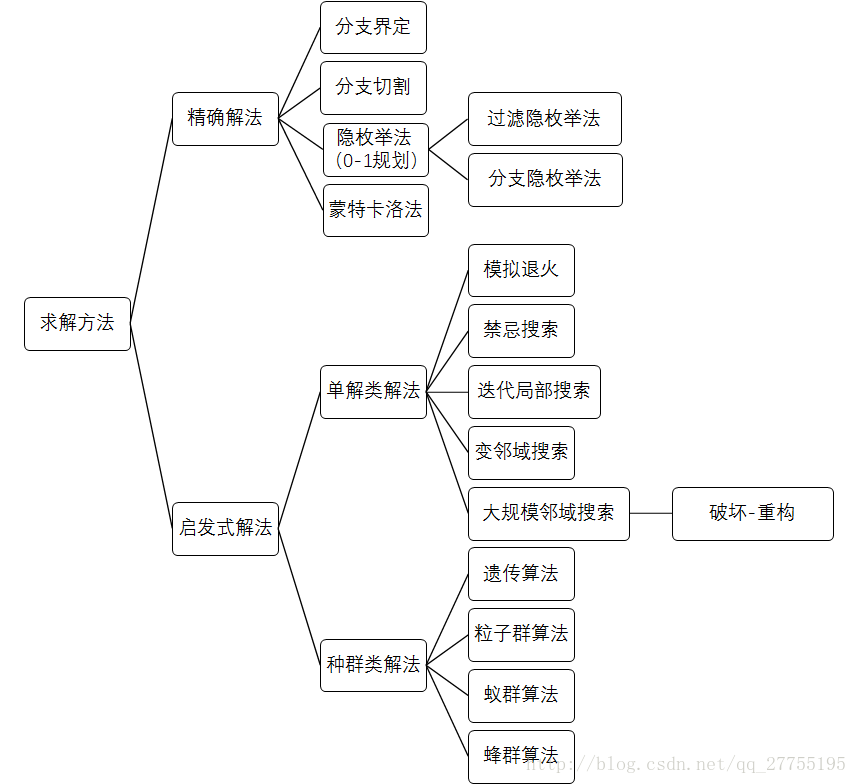
精确解法中遗漏了分支定价算法，入门列生成法和分支定价算法可以阅读罗纳德《运筹学》（肖永波译）第二版第13章
参考资料：

• 整数规划-求解方法整理
• 运筹学（原书第2版)