使用0-1变量将分段函数转换为线性约束


使用cplex提供的函数
连续线性分段约束
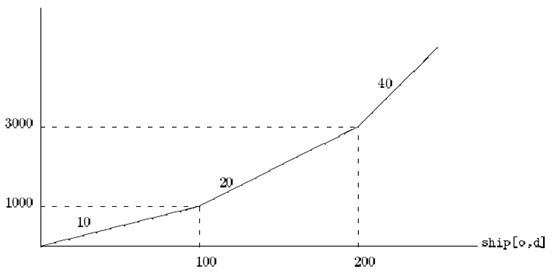
- 语法 piecewise
piecewise{10 -> 100;20 -> 200;40}(0,0) x;
piecewise{k1 -> x1;k2 -> x2;k3 -> x3;k4}(x0,y0) x
- 解释: x1之前斜率是k1,[x1, x2)期间斜率为k2,[x2, x3)期间值为k3,x3之后斜率为k4, (x0,y0)是分段函数中的某个点, x是变量
非连续线性分段
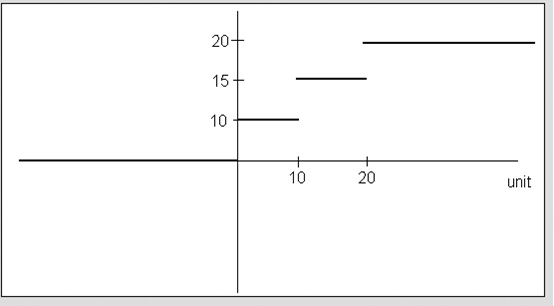
| Values of Unit | Cost |
|---|---|
| <0 | 0 |
| 0 to 10 | 10 |
| 10 to 20 | 15 |
| >20 | 20 |
- 语法
piecewise{0->0; 10->0; 0->10; 5->10; 0->20; 5->20; 0} (5,5) unit;
- 理解
使用分步函数
- 语法:stepFunction
F2 = stepwise{ 0->0; 100->20; 60->30; 100 };
- 解释:分步函数,0之前值为0,[0, 20)期间值为100,[20, 30)期间值为60,之后值为100:
python中使用分段函数的例子
import cplex
c = cplex.Cplex()
indices = c.variables.add(names=['y', 'x'])
idx = c.pwl_constraints.add(vary='y', varx='x',preslope=0.5, postslope=2.0,
breakx=[0.0, 1.0, 2.0], breaky=[0.0, 1.0, 4.0],
name='pwl1')
gurobi相关
在gurobi中只找到了在目标函数中采用近似线性化的方式来表达分段函数和非线性函数的方式。在csdn看到了相同的说法。但是可以使用SOS2约束进行转换,这个留待以后研究