线段树
1:概念:一看名字就知道是一棵树,但是这个树为什么有线段这两个字呢,原因就是他的思想——分治。
且它的结构大体上相似于一个2叉树。且每个子节点都相当于一个子区间,且父节点是子节点信息的总和,所以才叫线段树,如图这就是一个线段树。
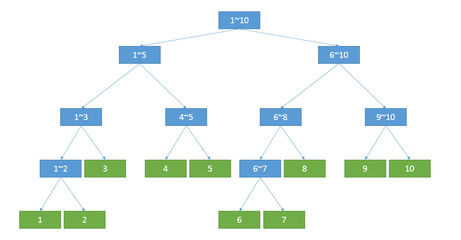
emmmm,图是从一个大佬从网上偷的那个图偷的。
2:功能及特点:
光知道了它的结构还不行
因为线段树是二叉树,所以每个父亲节点的编号i ,他的两个儿子的编号分别是2i和2i+1,如果当前节点为root,那么可以用位运算来取他的左右儿子分别是ans[root<<1],ans[root<<1|1];
就可以#define 一下
#define ls left,mid,root<<1 #define rs mid+1,right,root<<1|1
这个就可以在以后的函数中使用了。
先说一下所有变量的名称,l,r是指要修改的区间的左右端点,相反的left ,right则是当前的左右端点,ans数组是你输入的数据,下标则是在树中的位置。在下面的建树操作中我们就可以看见他是左区间等于右区间(即为子节点的时候)我们才输入他且输入的下标是他当前的节点下标
在树中的位置则用root来表示当前节点。lazy数组则是线段树的特点,正是有了它,才能加快速度。
l,r,left,right,ans[maxn<<2],lazy[maxn<<2],root;
接下来便是更新操作,看下面的操作之前,你要先理解透彻递归的含义——递便是不断向下调用自己,归则是把调用自己的值回溯上来。
所以你不能傻傻的建树,还需要回溯上来,就需要pushup—更新
il void pushup(ll root)//向上更新 { ans[root]=ans[root<<1]+ans[root<<1|1]; }
使用一棵线段树,首先要学会建树,建树就可以先从整棵树的根结点开始,向下二分,不断建树,且需要向上更新,如果你不懂的话,你就想这是一个DFS如果没到终点你就二分,到了终点你就记录每一个最低点的子节点得值,并回溯,因为根节点肯定是不断变化的,且应是先建根节点,再建子节点,再给子结点赋值,所以再将根节点的值更新,如果你不更新的话,它的根结点就加不上子节点了。
void build(ll left,ll right,ll root) { if(left==right) { scanf("%lld",&ans[root]); return; } ll mid=(left+right)>>1; build(ls);/二分 build(rs); pushup(root);//回溯过程 }
1:区间修改(包括单点修改)终于到正题了。
这就是我们要运用线段树的主要原因,因为他快,并且支持许许多多的操作。
那么对于区间操作,我们考虑引入一个名叫“lazy tag ”(懒标记)的东西——之所以称其“lazy ”,因为他真的很适合懒人使用。(单点修改不需要使用lazy tag)
假设现在老师要检查背诵了,你还不会背。
但是有一个设定,就是老师会告诉你你需不需要背。就像告诉你你需不需要被修改一样。
如果你不需要背,那你就可以不用背,这样你就可以节约时间去干别的事去了。
lazy标记便有这样一个功能。
区间修改便可以想象成一个或多个根节点向子节点传递lazy tag,既然已经传递了,那么本身肯定就一定加上了,本身的标记就可以清为零。
所以我们就可以写一个下传函数——pushdown
void pushdown(ll root,ll mid,ll left,ll right)// 下传。 { if(lazy[root]) { lazy[root<<1]+=lazy[root]; lazy[root<<1|1]+=lazy[root]; ans[root<<1]+=(mid-left+1)*lazy[root]; ans[root<<1|1]+=(right-mid)*lazy[root]; lazy[root]=0; } }
有了这个函数,线段树的所有最基本的操作就完成了。
到这我们就需要复习一下以前的变量,不然就会晕了。
l,r是要修改和查询的区间的端点。
如果当前区间被l,r包含。
那么就可以把当前节点的所有值都加上要增加的值,因为这个节点的本身的区间都要修改,所以就都加上就好了。
加的时候一定要将要增加的值乘上他的子节点的个数,因为他要加上所有节点的数。
如果没有完全包含,一定要先把它的标记下传,说明,下面的人需要背课文了(即下面的值需要修改了)
且那要修改的区间肯定有一段在左边或在右边,或两边都有。
就分别修改。
还要记住,更重要的是修改完之后一定要更新——pushup
void update(ll l,ll r,ll add,ll left,ll right,ll root) { if(l<=left&&r>=right) { lazy[root]+=add; ans[root]+=add*(right-left+1); return; } ll mid=(left+right)>>1; pushdown(root,mid,left,right); if(l<=mid) update(l,r,add,ls); if(r>=mid+1) update(l,r,add,rs); pushup(root); }
1:区间查询
其实这个跟区间修改差不多,就是把修改值变成了查询。
这里多出了一个变量——res,就是要返回的答案的值。
先判断是否包含,因为当前区间肯定是肯定是从大到小的,因此不存在要查询的区间一开始就包含当前区间,就不存在返回的res比实际的值小的情况。
ll query(ll l,ll r,ll left,ll right,ll root)//区间查询,l,r是要查询的区间,left,right,是当前区间 { ll res=0; if(l<=left&&r>=right) { return ans[root]; } ll mid=(left+right)>>1; pushdown(root,mid,left,right); if(l<=mid) res+=query(l,r,ls); if(r>=mid+1) res+=query(l,r,rs); return res; }
到此,线段树的基本操作就全部结束了
上标程——luogu P[3372]
#include<bits/stdc++.h> #define ll long long #define ls left,mid,root<<1 #define rs mid+1,right,root<<1|1 #define il inline using namespace std; const int maxn=100100; ll n,m,ans[maxn*4],lazy[maxn*4]; il void pushup(ll root)//向上更新 { ans[root]=ans[root<<1]+ans[root<<1|1]; } void build(ll left,ll right,ll root) { if(left==right) { scanf("%lld",&ans[root]); return; } ll mid=(left+right)>>1; build(ls); build(rs); pushup(root); } void pushdown(ll root,ll mid,ll left,ll right) { if(lazy[root]) { lazy[root<<1]+=lazy[root]; lazy[root<<1|1]+=lazy[root]; ans[root<<1]+=(mid-left+1)*lazy[root]; ans[root<<1|1]+=(right-mid)*lazy[root]; lazy[root]=0; } } void update(ll l,ll r,ll add,ll left,ll right,ll root) { if(l<=left&&r>=right) { lazy[root]+=add; ans[root]+=add*(right-left+1); return; } ll mid=(left+right)>>1; pushdown(root,mid,left,right); if(l<=mid) update(l,r,add,ls); if(r>=mid+1) update(l,r,add,rs); pushup(root); } ll query(ll l,ll r,ll left,ll right,ll root)//区间查询,l,r是要查询的区间,left,right,是当前区间 { ll res=0; if(l<=left&&r>=right) { return ans[root]; } ll mid=(left+right)>>1; pushdown(root,mid,left,right); if(l<=mid) res+=query(l,r,ls); if(r>=mid+1) res+=query(l,r,rs); return res; } int main() { scanf("%lld%lld",&n,&m); ll p,x,y,k; build(1,n,1); while(m--) { scanf("%lld",&p); if(p==1) { scanf("%lld%lld%lld",&x,&y,&k); update(x,y,k,1,n,1); } else { scanf("%lld%lld",&x,&y); printf("%lld ",query(x,y,1,n,1)); } } return 0; }