

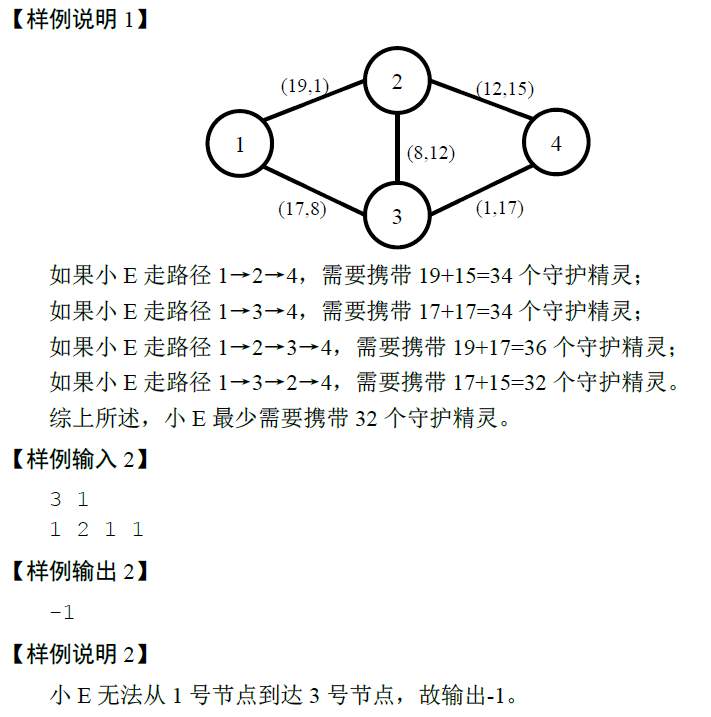
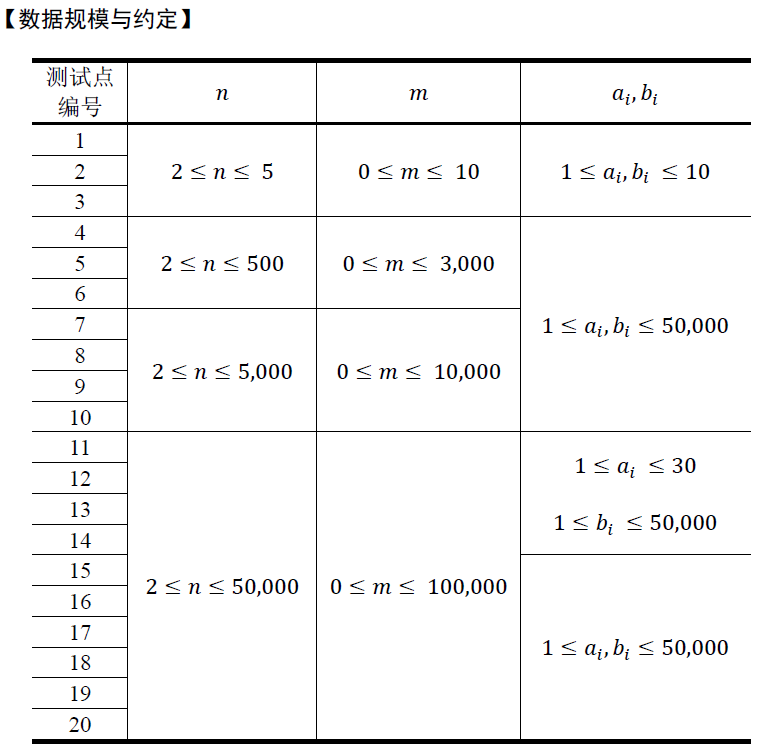
这道题正解其实是LCT,然而貌似SPFA也可以成功水过,所以根本不知道LCT的我只能说SPFA了。
这道题最大的限制是两种精灵就意味着一条道可能有两个权值,因此我们需要去将其中一个固定,然后再推另一个权值,也就是说,我们可以,枚举每一条边的a,然后只走a值不大于他的边。
然而并没有那么容易,本题数据极大,这种算法一半分都拿不到,因此我们需要别的优化,首先,我们可以现将每个边按照a的大小进行排序,然后从小到大边枚举边加边,这时dis数组就不必去每次spfa都清空了,而且每次枚举边都可以在原来的图的基础上直接加边,且当前边一定都是能走的边,不必再算上那些不满足要求的边了,可以大大地优化是时间复杂度。

1 #include<iostream> 2 #include<cstdlib> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 #include<map> 7 #include<queue> 8 #include<string> 9 #include<cmath> 10 using namespace std; 11 int n,m,zz,a[500005]; 12 struct ro{ 13 int to,from; 14 int next; 15 int a,b; 16 }road[2000005]; 17 struct no{ 18 int a,b,from,to; 19 }node[200004]; 20 void build(int x,int y,int z,int zx) 21 { 22 zz++; 23 road[zz].from=x; 24 road[zz].to=y; 25 road[zz].next=a[x]; 26 road[zz].a=z; 27 road[zz].b=zx; 28 a[x]=zz; 29 } 30 int dis[500005]; 31 queue<int> q1; 32 bool rd[500005]; 33 int ans=0x7fffffff; 34 void spfa(int x0,int y0,int z,int zx){ 35 rd[x0]=rd[y0]=1; 36 q1.push(x0); 37 q1.push(y0); 38 while(!q1.empty()) 39 { 40 int x=q1.front(); 41 q1.pop(); 42 rd[x]=0; 43 for(int i=a[x];i>0;i=road[i].next) 44 { 45 int y=road[i].to; 46 47 if(dis[y]>max(dis[x],road[i].b)) 48 { 49 dis[y]=max(dis[x],road[i].b); 50 if(!rd[y]) 51 { 52 q1.push(y); 53 rd[y]=1; 54 } 55 } 56 } 57 } 58 int an=0; 59 an=dis[n]; 60 if(an!=dis[0]&&ans>an+z) 61 ans=an+z; 62 } 63 int px(no a,no b) 64 { 65 return a.a<b.a; 66 } 67 int main(){ 68 memset(dis,0x7f,sizeof(dis)); 69 scanf("%d%d",&n,&m); 70 for(int i=1;i<=m;i++) 71 { 72 int x,y,z,zx; 73 scanf("%d%d%d%d",&x,&y,&z,&zx); 74 node[i].a=z; 75 node[i].b=zx; 76 node[i].to=y; 77 node[i].from=x; 78 } 79 sort(node+1,node+m+1,px); 80 dis[1]=0,rd[1]=1; 81 q1.push(1); 82 for(int i=1;i<=m;i++) 83 { 84 int bj=i; 85 build(node[i].from,node[i].to,node[i].a,node[i].b); 86 build(node[i].to,node[i].from,node[i].a,node[i].b); 87 spfa(node[i].from,node[i].to,node[i].a,node[i].b); 88 } 89 if(ans==0x7fffffff) ans=-1; 90 printf("%d ",ans); 91 // while(1); 92 return 0; 93 }
