自然对数e
假如你有一块钱,放银行,银行给你100%的利率也就是说存一年后变成两块钱。
那么现在问题来了,假如我半年取一次,取完再放入银行存半年,那么我就可以得到(1+0.5)²也就是2.25,比两块钱还多,
假如我分1/4年存取一次呢,那么就是(1+0.25)的四次方,约为2.44,又更多了。
假如我无限分割下去,我能得到无限的本息吗?
答案是不能,(1+1/∞)的无穷次方等于e,约为2.71828,这就是自然对数。
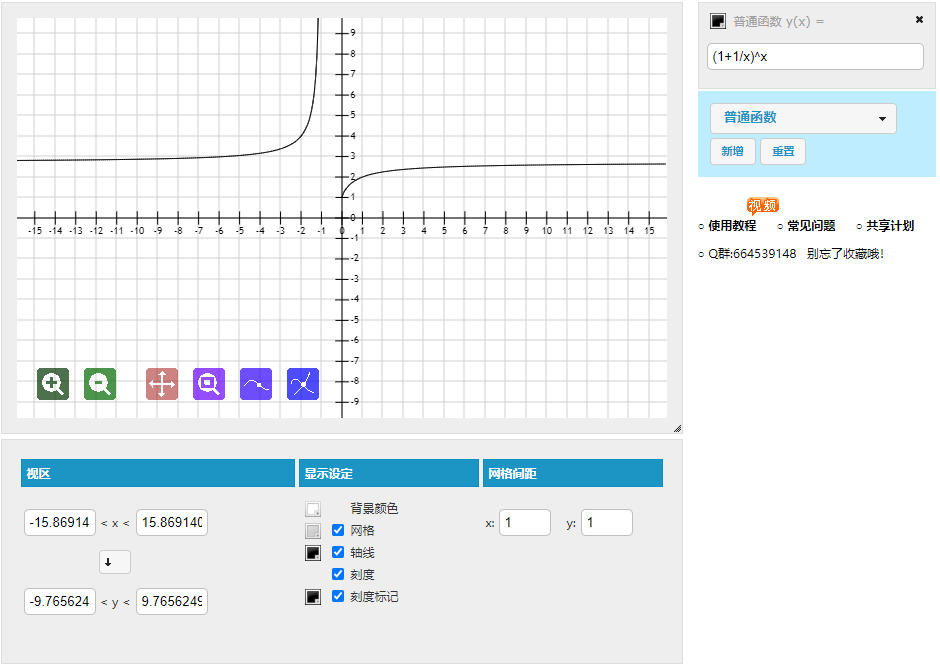
函数f(x)=(1+1/x)^x有定义,当x趋向于无穷大时,此函数有极限,且极限是一无理数,把这一极限值记为e,作为自然对数的底,约为2.718281828.