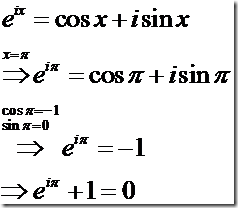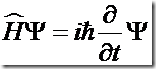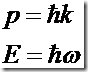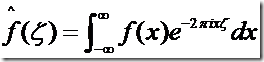原文 Top Ten Greatest Equations Ever
本文内容
- No.1 麦克斯韦方程组
- No.2 欧拉方程
- No.3 牛顿第二定律
- No.4 毕达哥拉斯定理
- No.5 薛定谔方程
- No.6 波尔兹曼方程
- No.7 最小作用量原理
- No.8 德布罗意方程组
- No.9 傅立叶变换
- No.10 爱因斯坦场广义相对论方程
- 参考资料
2004 年 10 月,罗伯特在英国科学期刊《物理世界》让读者投票评选“最伟大的公式”,罗伯特工作在纽约州立大学石溪分校哲学系,而且是一个历史学家在布鲁克海文国家实验室,共有 120 个人进行了回应,提出了 50 种不同的方程,他还要求他们解释为什么。
不得不感叹,那些伟人耗尽一生,最终写下一个等号;更不得不感叹,在这些公式中的确看见了美,看见了上帝……
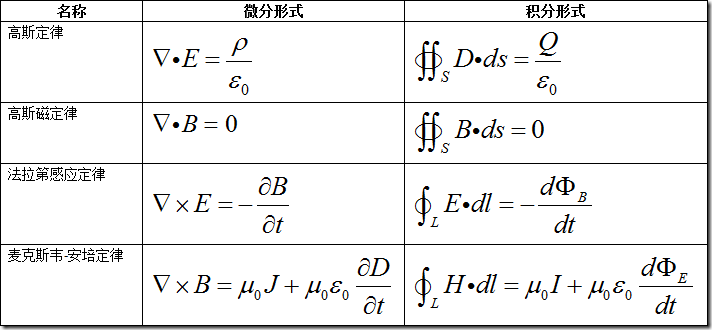
No.1 麦克斯韦方程组
麦克斯韦方程组(Maxwell's four equations),描述了电磁场在空间和时间上如何变化。
麦克斯韦方程组,是英国物理学家詹姆斯·麦克斯韦在 19 世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。它由四个方程组成,从该方程组,可以推论出光波是电磁波。麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程,并发展出现代的电力科技与电子科技。麦克斯韦 1865 年提出的最初形式由 20 个等式和 20 个变量组成,于 1873 年尝试用四元数来表达,但未成功。
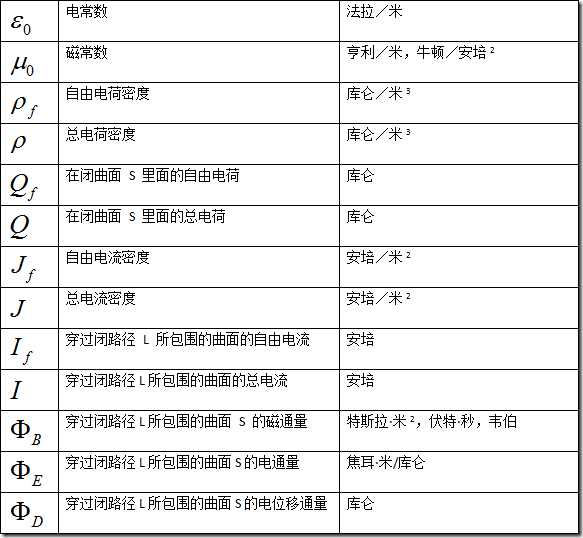
微观麦克斯韦方程组,以总电荷和总电流为源头的表述:
宏观麦克斯韦方程组,以自由电荷和自由电流为源头的表述:
表 1 麦克斯韦方程组物理意义和单位
No.2 欧拉方程
欧拉方程(Euler's equation),描述了流体动力学中动量流和力密度之间的关系。
欧拉恒等式,如下所示:
其中,e 是自然指数的底,i 是虚数单位,π 是圆周率。
上式是复分析(复分析是研究复函数,特别是亚纯函数和复解析函数的数学理论)欧拉公式的特殊情况。这个公式的巧妙之处在于,它没有任何多余的内容,将数学中最基本的 e、i、π 放在同一个式子中,同时,加入了数学也是哲学中最重要的 0 和 1,再以简单的加号相连。该恒等式第一次出现于 1748 年莱昂哈德·欧拉在洛桑出版的书《Introductio》。理查德·费曼称该恒等式为“数学最奇妙的公式”。高斯曾经说:“一个人第一次看到这个公式而不感到它的魅力,他不可能成为数学家。”
欧拉是历史上最多产的数学家,各个领域(包含数学的所有分支及力学、光学、音响学、水利、天文、化学、医药等)最多著作的学者。数学史上称十八世纪为“欧拉时代”。欧拉生于瑞士,31 岁丧失了右眼视力,59 岁双眼失明,但他性格乐观,有惊人的记忆力及集中力。他一生谦逊,很少用自己的名字给他发现的东西命名,除了一个——e。
关于 e,有个笑话,一家精神病院,有个病患整天对着别人说,“我微分你、我微分你。”这些病患都有一点简单的微积分概念,总以为有一天自己会像一般多项式函数般,被微分到变成零而消失,因此对他避之不及,然而某天他却遇上了一个不为所动的人,他很意外,而这个人淡淡地对他说,“我是e的x次方。”
欧拉公式是在复分析领域的公式,将三角函数与复数指数函数相关联。欧拉恒等式是欧拉公式的特殊情况,对任意实数 x,都存在
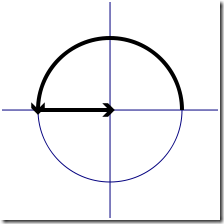
从 e0 = 1 开始,以相对速度 i,走 π 长时间,加 1,则到达原点。
No.3 牛顿第二定律
牛顿第二定律(Newton Second Law),描述了物体加速度的大小跟物体受到的作用力成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同。
有史以来最伟大的、无处其二的科学巨作《自然哲学的数学原理》,被认为是经典物理学中最伟大的定律。动力的所有基本方程都可由它通过微积分推导出来。
No.4 毕达哥拉斯定理
毕达哥拉斯定理(Pythagoras Theorum),或勾股定理,描述了在任何直角三角形,其斜边的平方等于两个直角边的平方和。
No.5 薛定谔方程
薛定谔方程(Schrödinger's equation),描述了量子力学系统的时间依赖性,是量子力学的基础方程之一,它以发表者奥地利物理学家埃尔温·薛定谔而命名。由于对量子力学的杰出贡献,薛定谔获得 1933 年诺贝尔物理奖,官方评价:“薛定谔方程是世界原子物理学文献中应用最广泛、影响最大的公式。”
“薛定谔方程”可以指广义形式的薛定谔方程,也可指具体形式的薛定谔方程。广义形式的薛定谔方程名如其实,可以应用于广泛量子力学领域,表达从狄拉克方程到量子场论的各种方程,只要将哈密顿算符的各种复杂表达式代入就行了。通常,具体形式的薛定谔方程所描述的系统是实际系统的简化近似模型,这是为了要避开不必要的复杂数学运算。对于大多数案例,所得到的结果相当准确;但是对于相对论性案例,结果则并不令人满意。
No.6 波尔兹曼方程
波尔兹曼方程(Boltzmann equation),描述了一个流体中粒子的统计分布,粒子位置和动量概率分布在相空间中的密度分布云图随时间和空间的变化。
No.7 最小作用量原理
最小作用量原理(least action principle),或更精确地,平稳作用量原理(stationary action principle),在现代物理学里,这原理非常重要,在相对论、量子力学、量子场论里,都有广泛的用途。在现代数学里,这原理是莫尔斯理论的研究焦点。
No.8 德布罗意方程组
德布罗意方程组(De Broglie equation),可见波长和动量成反比;频率和动能成正比之关系。
这个东西也挺牛,高中物理学到光学的话很多概念跟它是远亲。简要地说,德布罗意觉得电子不仅是一个粒子,也是一种波,它还有 “波长”。于是就搞出了这个物质波方程,表达了波长、能量等之间的关系。德布罗意获得了 1929 年诺贝尔物理学奖。
No.9 傅立叶变换
傅立叶变换(Fourier Transformation),描述了 将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。
傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值谱——显示与频率对应的幅值大小)。
No.10 爱因斯坦场广义相对论方程
爱因斯坦场方程广义相对论(General Relativity),是一种关于引力的理论,物质之间的引力来自于时空的弯曲。爱因斯坦在 1907 年到 1915 年完成。
在广义相对论出现之前的200多年间,牛顿万有引力定律被广泛接受,它成功地解释了物质之间的引力作用。在牛顿定律中,引力来自大质量物质之间的相互吸引。虽然牛顿也不知道这种力的本质,但它在描述运动时却非常成功。
但是,实验和观测都显示,爱因斯坦对引力的描述能够解释多个由牛顿定律无法解释的现象,比如水星和其他行星轨道的反常进动。广义相对论还预言了一些关于引力的显著效应,如引力波和引力透镜,还有引力场引发的时间膨胀。很多预言都已经被实验所证实,还有一些正在探索中。广义相对论已经成为现代天体物理学的重要工具,它提供了现在理解黑洞的基础。其强大的引力也使一些天体(如活动星系核和X射线双星)发射出强烈的辐射。广义相对论也是宇宙学的标准大爆炸模型的理论框架中的一部分。
然而,到现在仍然有大量的问题没有解决,其最根本的是广义相对论如何和量子力学结合而产生一个完整一致的量子引力理论。
另外,早在 1998 年,David Wells 在《The mathematical Intelligencer》(Vol.10 No.4 1988, P.30-31) 针对数学界发出了有 24 个选项的问卷——“最美丽的数学定理(Which is the most beautiful?)”,最后他收回了 76 份完整问卷,去掉无效的,由 68 份评分统计结果。并在之后的文章“Are these the most beautiful?”(Vol.12, No 3, 1990, P. 37-41),公布了结果。
参考资料
- Top Ten Greatest Equations Ever
- 麦克斯韦方程
- David Wells (1988), Which is the most beautiful?, Mathematical Intelligencer, Vol.10 No.4 pp.30-31
- David Wells (1990), Are these the most beautiful?, Mathematical Intelligencer, Vol.12, No 3, pp. 37-41
- Wiki_欧拉恒等式
- Wiki_素数
- 傅里叶变换