一、如何改进一个机器学习算法
假设你已经训练出一个机器学习算法,但是效果不太好,那么有以下几种改进方法:
1、获得更多的训练数据
2、选用更少的特征
3、增加特征量
4、增加高次项
5、增大或减小正则化参数lambda的值
很多人只是随机选择上述方法的一种,即浪费时间又没有效果。所以接下来会介绍模型的评估及机器学习的诊断法。
二、模型评估(Evaluating a Hypothesis)
1、评估假设:
一个训练误差最小的假设有时并不是一个好的假设,而且当特征过多时,我们很难画出假设函数来观察。
有一种标准方法,将训练数据分成两部分,第一部分是训练集,第二部分是测试集,一般是7:3左右。
2、具体步骤:
那么我们训练模型的流程可以有如下两个部分:
(1)使用训练集来训练模型参数θ,(最小化代价函数Jtrain(Θ))
(2)使用测试集来计算误差Jtest(Θ)
对于线性回归来说,误差:

对于逻辑回归来说,误差:
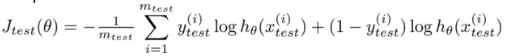
三、模型选择和训练、验证、测试集(Model selection and train/validation/test sets)
1、不使用验证集的模型选择:
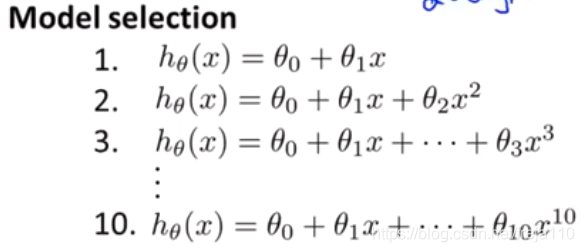
一般的,是选择J最小的那个模型,但是这样只能使得模型对于测试集数据的误差较小,而对于其他数据的泛化效果并不好。因而这种方法并不能很好的验证误差。
2、使用验证集(Cross Validation Set)**
为了解决泛用性问题,我们引入了第三个数据集,交叉验证集。将其作为训练集和验证集之间的中间层来训练多项式次数d,然后用测试集进行测试,我们就能得到一个没有针对测试集“特殊优化”过的误差。比例为:训练集60%,交叉验证集20%,测试集20%。
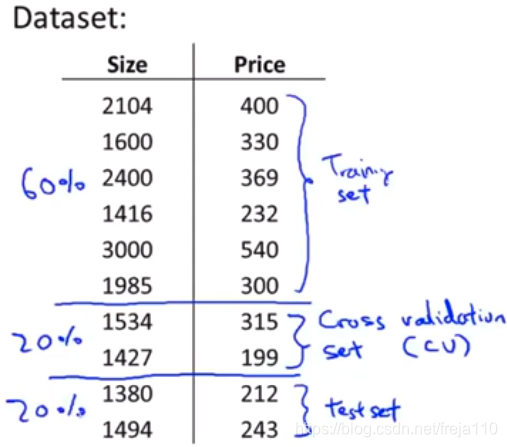
三种数据集的误差如下:

四、诊断偏差与方差(Diagnosing Bias vs. Variance)
在这一节里,我们要寻找多项式次数d与欠拟合、过拟合之间的关系。
首先,我们需要确认,偏差与方差是否是影响我们取得好结果的问题因素:
高偏差意味着欠拟合,是形容数据分散程度的,对象是单个模型
高方差意味着过拟合,形容数据跟我们期望的中心差得有多远,对象是多个模型
我们需要找到一个好方法来平衡他们。
那么我们根据下图可以量化地判断过拟合、欠拟合,以及找出参数d的最优解。
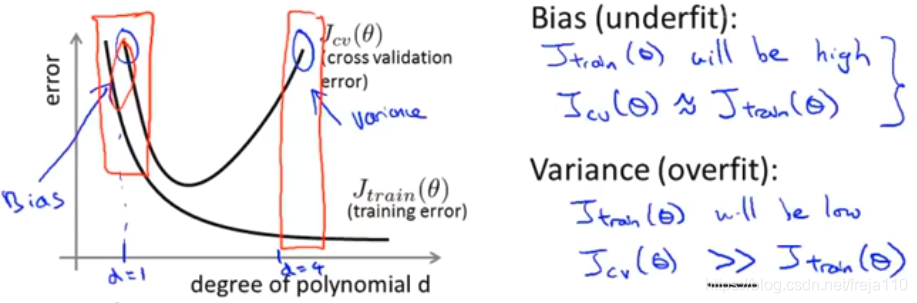
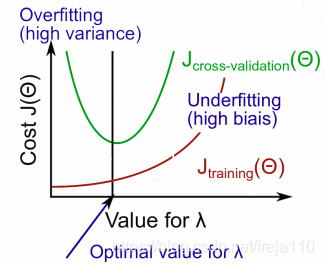
五、正则化和偏差、方差(Regularization and Bias/Variance)
这一节,我们要寻找正则化参数λ与偏差、方差的关系。
较大的λ:高偏差(欠拟合)
适中的λ:没有大问题
较小的λ:高方差(过拟合)
一个大的λ值惩罚了所有θ参数,这极大地简化了函数曲线,所以会导致欠拟合。
那么我们根据下图可以量化地判断过拟合、欠拟合,以及找出lambda的最优解
六、学习曲线(Learning Curves)
使用学习曲线可以有效的判断一个学习算法是否有偏差方差或者二者都有。
1、学习曲线的绘制:
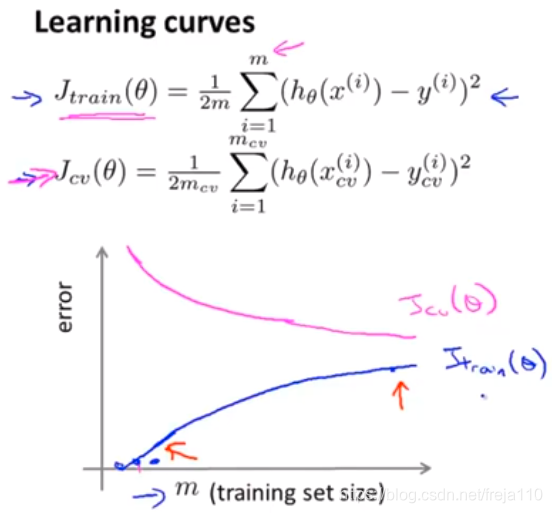
绘制出训练集和交叉验证集的平均误差平方和随着样本数量m变化而变化的曲线。
2、高偏差情况下的学习曲线
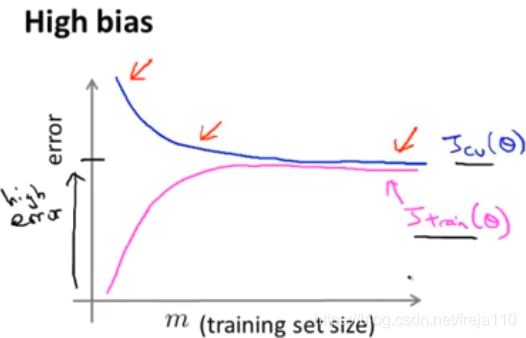
结论:如果一个学习算法有高偏差,增加训练样本对改善算法表现无益。
**
3、高方差情况下的学习曲线
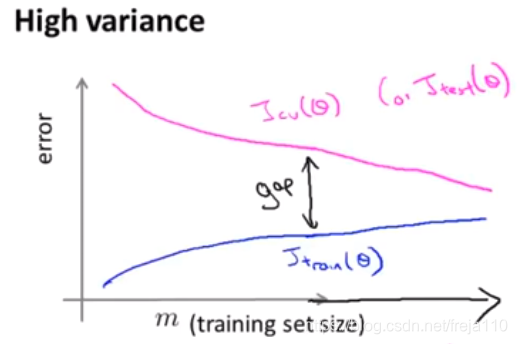
结论:如果一个学习算法有高方差,增加训练样本对改善算法有帮助。
七、总结(revisited)
如何调试学习算法
1、获得更多的训练数据:修正高方差情况
2、选用更少的特征:修正高方差
3、增加特征量:修正高偏差
4、增加高次项:修正高偏差
5、减小正则化参数lambda的值:修正高偏差
6、增大正则化参数lambda的值:修正高方差
八、神经网络的诊断
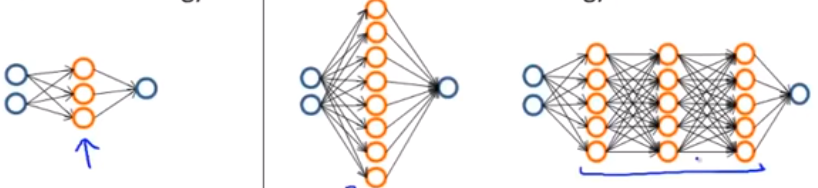
一般的,选择左侧较简单的神经网络,往往会出现欠拟合问题,计算量小
选择右侧较大的神经网络结构,有时会出现过拟合问题,计算量大