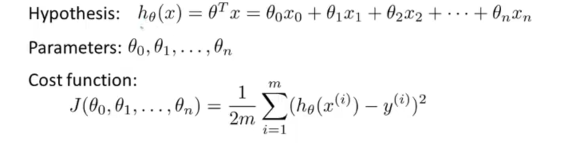
hθ(x)是一个假设函数,我们要求得参数向量θ使得损失函数J(θ)最低,我们可以看出,参数θ向量中包含多个变量(θ0,θ1,θ2,θ3),我们可以先选取一个参数,然后把
其他参数暂时作为常量,对J(θ)求导,得到改参数变量的下降方向,然后乘以学习系数便得到下降的步宽。利用以下公式更新参数:

也就是:
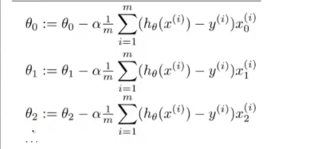
当所有参数都遍历一遍后即完成一次下落,如果学习系数足够小,最终可使损失函数J(θ)=0。此时的参数即为最佳参数。
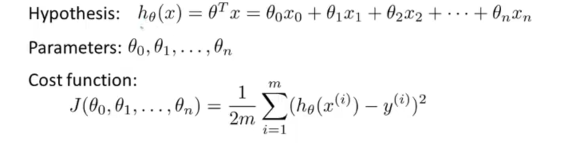
hθ(x)是一个假设函数,我们要求得参数向量θ使得损失函数J(θ)最低,我们可以看出,参数θ向量中包含多个变量(θ0,θ1,θ2,θ3),我们可以先选取一个参数,然后把
其他参数暂时作为常量,对J(θ)求导,得到改参数变量的下降方向,然后乘以学习系数便得到下降的步宽。利用以下公式更新参数:

也就是:
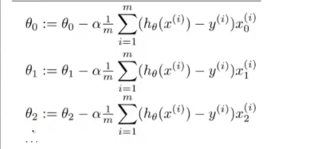
当所有参数都遍历一遍后即完成一次下落,如果学习系数足够小,最终可使损失函数J(θ)=0。此时的参数即为最佳参数。