Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4], Output: 6 Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
题意:
求最大子数组和
思路:
开一个一维dp
原理:任何数加负数肯定比原值小
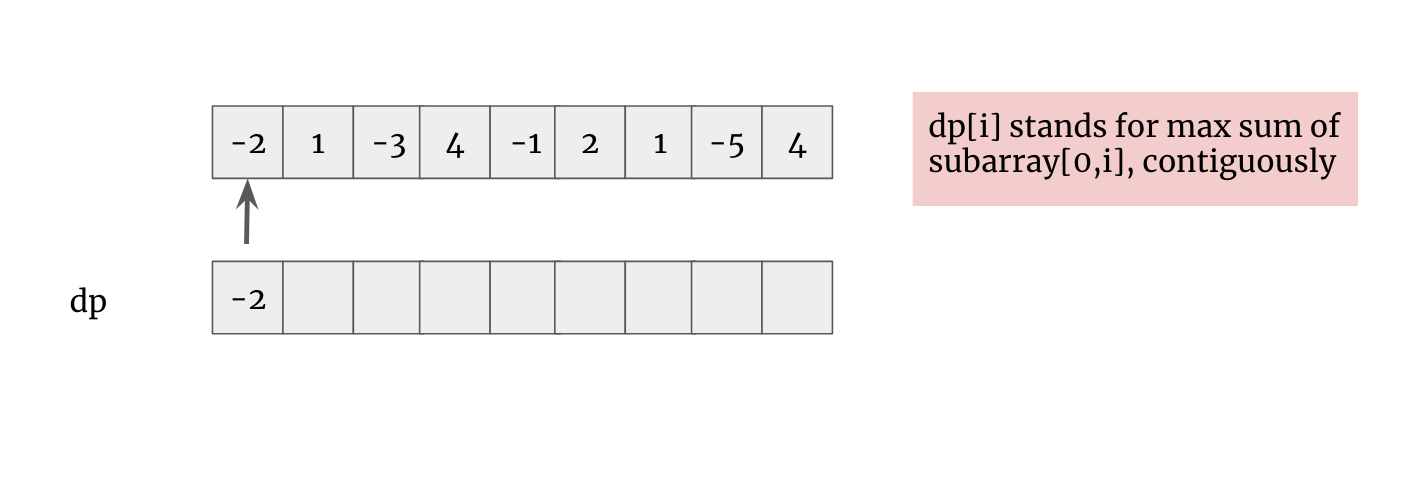
1. dp[i] stands for max sum of subarray[0,i] (nums[i] must be used)
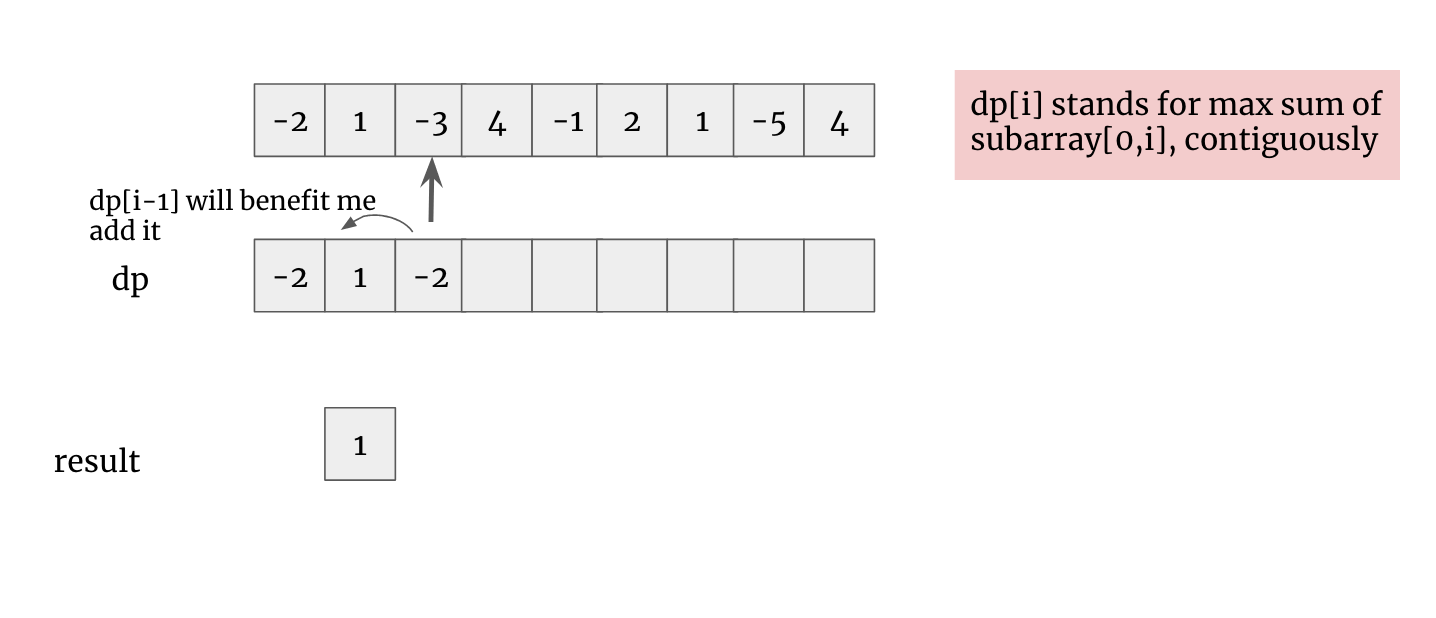
2. coz any negative will worsen final result. supposing I am standing at current nums[i], if previous sum dp[i-1] > 0, it will benifit result, then we wrap dp[i-1] + nums[i] to dp[i]
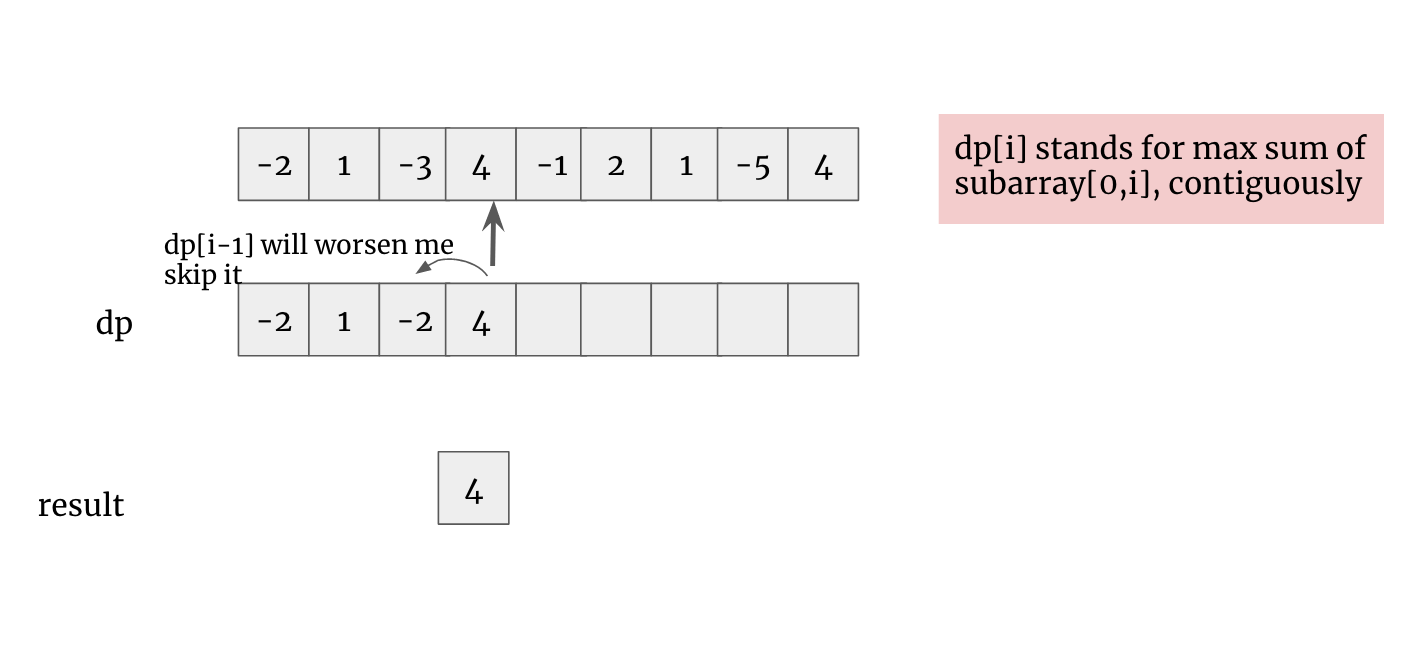
otherwise, if dp[i-1] < 0, we only keep nums[i]
3. the dp function will be :
dp[i] = dp[i-1] >0 ? dp[i-1] + num[i] : num[i]


code
1 class Solution { 2 public int maxSubArray(int[] nums) { 3 // dp[i]: max sum of subarray from 0 to i 4 int[] dp = new int[nums.length]; 5 // initiliaze 6 dp[0] = nums[0]; 7 int result = nums[0]; 8 9 for(int i = 1; i < nums.length; i++){ 10 // negative value will worsen result, if dp[i-1] < 0, we only keep nums[i] 11 dp[i] = dp[i-1] > 0 ? dp[i-1] + nums[i] : nums[i]; 12 // update max result 13 result = Math.max(result, dp[i]); 14 } 15 return result; 16 } 17 }
思路
优化空间为O(1)
Coz result is only related to previous sum.
We can use a variable to track previous sum.
代码
1 public class MaximumSubarray { 2 public int maxSubArray(int[] nums) { 3 // initialize 4 int result = Integer.MIN_VALUE; 5 // reset it to 0 if it's less than 0. 6 int sum = 0; 7 for (int n : nums) { 8 // if sum < 0, we only keep n; if sum > 0, sum to be added to benefit result 9 sum = n + Math.max(sum, 0); 10 // update max result 11 result = Math.max(result, sum); 12 } 13 return result; 14 } 15 }