You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: [1,2,3,1] Output: 4 Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3). Total amount you can rob = 1 + 3 = 4.
Example 2:
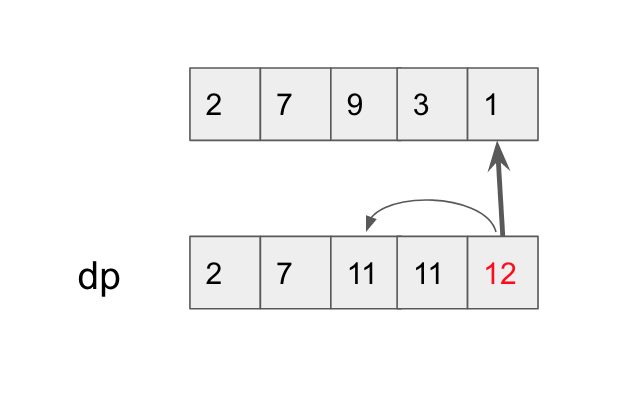
Input: [2,7,9,3,1] Output: 12 Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1). Total amount you can rob = 2 + 9 + 1 = 12.
题意:
给定一个小偷和一排房子。偷了相邻俩屋子就会被抓,问怎么偷最来钱。
Solution1: DP
dp[i]: represent the max amount of money we can rob up to and including the current house
WHICH MEANS
dp[i] = max of robbing the current house and however much money we had 2 houses before,
or simply continue on with the max amount of money we had robbed up to the previous house


code
1 class Solution { 2 public int rob(int[] nums) { 3 if (nums == null || nums.length == 0) return 0; 4 if (nums.length == 1) return nums[0]; 5 if (nums.length == 2) return Math.max(nums[0], nums[1]); 6 7 int[] dp = new int[nums.length]; 8 dp[0] = nums[0]; 9 dp[1] = Math.max(nums[0], nums[1]); 10 for(int i = 2; i < nums.length; i++){ 11 dp[i] = Math.max(nums[i]+dp[i-2], dp[i-1]); 12 } 13 return dp[nums.length-1]; 14 } 15 }