[leetcode]62. Unique Paths 不同路径(求路径和)

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

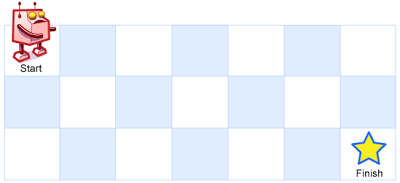
Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

题目

给定MxN棋盘，只允许从左上往右下走，每次走一格。共有多少种走法？

思路

Matrix DP（二维DP） 问题

1. 初始化

预处理第一个row： dp[0][j] = 1  因为从左上起点出发，往右走的每一个unique path都是1

预处理第一个col：   dp[i][0]= 1  因为从左上起点出发，往下走的每一个unique path 都是1 

2. 转移方程

因为要求所有possible unique paths之和

dp[i][j] 要么来自dp[i-1][j] 要么来自dp[i][j-1]

代码

class Solution {
    public int uniquePaths(int m, int n) {
        int[][]dp = new int[n][m]; // [row][col]
        
        // 预处理第一个col
        for(int i= 0; i < n; i++){
            dp[i][0] = 1;
        }  
        //预处理第一个row
        for(int j=0; i < m; i++){
            dp[0][j] = 1;
        }
        for(int i= 1; i < n; i++){
            for(int j= 1; j < m; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[n-1][m-1];
    }
}