==============
接上文《 线程基础:多任务处理(12)——Fork/Join框架(基本使用)》
3. 使用Fork/Join解决实际问题
之前文章讲解Fork/Join框架的基本使用时,所举的的例子是使用Fork/Join框架完成1-1000的整数累加。这个示例如果只是演示Fork/Join框架的使用,那还行,但这种例子和实际工作中所面对的问题还有一定差距。本篇文章我们使用Fork/Join框架解决一个实际问题,就是高效排序的问题。
3-1. 使用归并算法解决排序问题
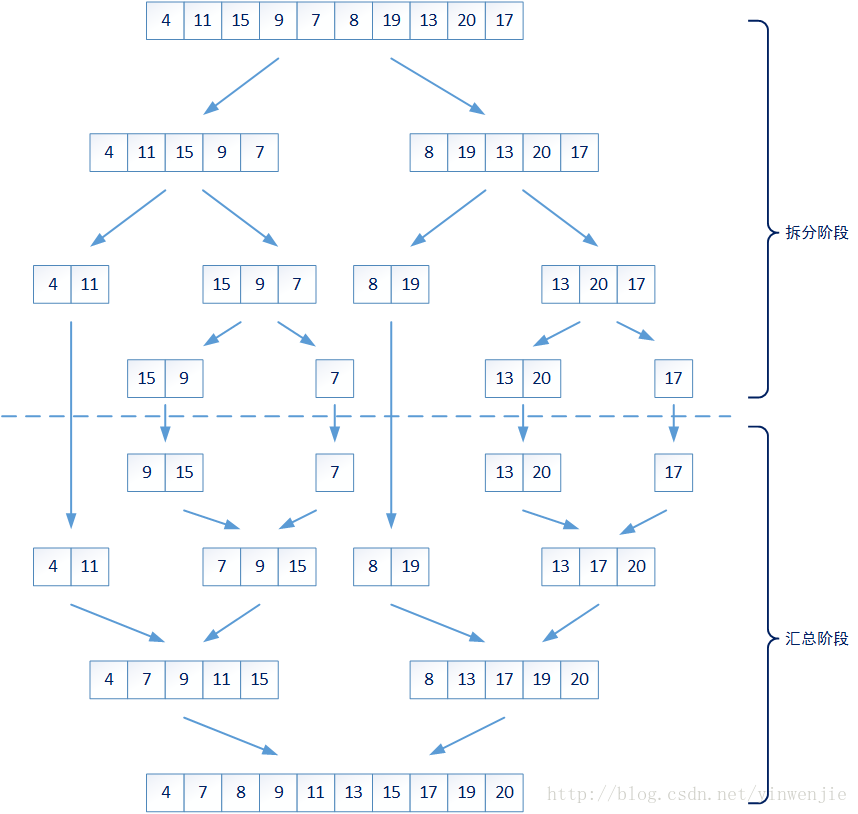
排序问题是我们工作中的常见问题。目前也有很多现成算法是为了解决这个问题而被发明的,例如多种插值排序算法、多种交换排序算法。而并归排序算法是目前所有排序算法中,平均时间复杂度较好(O(nlgn)),算法稳定性较好的一种排序算法。它的核心算法思路将大的问题分解成多个小问题,并将结果进行合并。
整个算法的拆分阶段,是将未排序的数字集合,从一个较大集合递归拆分成若干较小的集合,这些较小的集合要么包含最多两个元素,要么就认为不够小需要继续进行拆分。
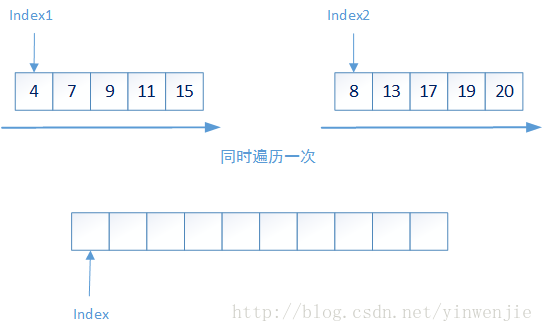
那么对于一个集合中元素的排序问题就变成了两个问题:1、较小集合中最多两个元素的大小排序;2、如何将两个有序集合合并成一个新的有序集合。第一个问题很好解决,那么第二个问题是否会很复杂呢?实际上第二个问题也很简单,只需要将两个集合同时进行一次遍历即可完成——比较当前集合中最小的元素,将最小元素放入新的集合,它的时间复杂度为O(n):
以下是归并排序算法的简单实现:
package test.thread.pool.merge;
import java.util.Arrays;
import java.util.Random;
/**
* 归并排序
* @author yinwenjie
*/
public class Merge1 {
private static int MAX = 10000;
private static int inits[] = new int[MAX];
// 这是为了生成一个数量为MAX的随机整数集合,准备计算数据
// 和算法本身并没有什么关系
static {
Random r = new Random();
for(int index = 1 ; index <= MAX ; index++) {
inits[index - 1] = r.nextInt(10000000);
}
}
public static void main(String[] args) {
long beginTime = System.currentTimeMillis();
int results[] = forkits(inits);
long endTime = System.currentTimeMillis();
// 如果参与排序的数据非常庞大,记得把这种打印方式去掉
System.out.println("耗时=" + (endTime - beginTime) + " | " + Arrays.toString(results));
}
// 拆分成较小的元素或者进行足够小的元素集合的排序
private static int[] forkits(int source[]) {
int sourceLen = source.length;
if(sourceLen > 2) {
int midIndex = sourceLen / 2;
int result1[] = forkits(Arrays.copyOf(source, midIndex));
int result2[] = forkits(Arrays.copyOfRange(source, midIndex , sourceLen));
// 将两个有序的数组,合并成一个有序的数组
int mer[] = joinInts(result1 , result2);
return mer;
}
// 否则说明集合中只有一个或者两个元素,可以进行这两个元素的比较排序了
else {
// 如果条件成立,说明数组中只有一个元素,或者是数组中的元素都已经排列好位置了
if(sourceLen == 1
|| source[0] <= source[1]) {
return source;
} else {
int targetp[] = new int[sourceLen];
targetp[0] = source[1];
targetp[1] = source[0];
return targetp;
}
}
}
/**
* 这个方法用于合并两个有序集合
* @param array1
* @param array2
*/
private static int[] joinInts(int array1[] , int array2[]) {
int destInts[] = new int[array1.length + array2.length];
int array1Len = array1.length;
int array2Len = array2.length;
int destLen = destInts.length;
// 只需要以新的集合destInts的长度为标准,遍历一次即可
for(int index = 0 , array1Index = 0 , array2Index = 0 ; index < destLen ; index++) {
int value1 = array1Index >= array1Len?Integer.MAX_VALUE:array1[array1Index];
int value2 = array2Index >= array2Len?Integer.MAX_VALUE:array2[array2Index];
// 如果条件成立,说明应该取数组array1中的值
if(value1 < value2) {
array1Index++;
destInts[index] = value1;
}
// 否则取数组array2中的值
else {
array2Index++;
destInts[index] = value2;
}
}
return destInts;
}
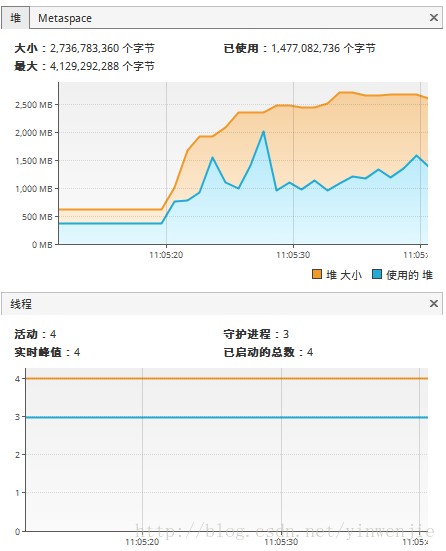
}以上归并算法对1万条随机数进行排序只需要2-3毫秒,对10万条随机数进行排序只需要20毫秒左右的时间,对100万条随机数进行排序的平均时间大约为160毫秒(这还要看随机生成的待排序数组是否本身的凌乱程度)。可见归并算法本身是具有良好的性能的。使用JMX工具和操作系统自带的CPU监控器监视应用程序的执行情况,可以发现整个算法是单线程运行的,且同一时间CPU只有单个内核在作为主要的处理内核工作:
JMX中观察到的线程情况:
CPU的运作情况:
3-2. 使用Fork/Join运行归并算法
但是随着待排序集合中数据规模继续增大,以上归并算法的代码实现就有一些力不从心了,例如以上算法对1亿条随机数集合进行排序时,耗时为27秒左右。
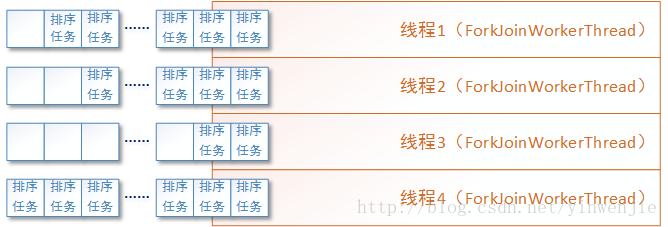
接着我们可以使用Fork/Join框架来优化归并算法的执行性能,将拆分后的子任务实例化成多个ForkJoinTask任务放入待执行队列,并由Fork/Join框架在多个ForkJoinWorkerThread线程间调度这些任务。如下图所示:
以下为使用Fork/Join框架后的归并算法代码,请注意joinInts方法中对两个有序集合合并成一个新的有序集合的代码,是没有变化的可以参见本文上一小节中的内容。所以在代码中就不再赘述了:
......
/**
* 使用Fork/Join框架的归并排序算法
* @author yinwenjie
*/
public class Merge2 {
private static int MAX = 100000000;
private static int inits[] = new int[MAX];
// 同样进行随机队列初始化,这里就不再赘述了
static {
......
}
public static void main(String[] args) throws Exception {
// 正式开始
long beginTime = System.currentTimeMillis();
ForkJoinPool pool = new ForkJoinPool();
MyTask task = new MyTask(inits);
ForkJoinTask<int[]> taskResult = pool.submit(task);
try {
taskResult.get();
} catch (InterruptedException | ExecutionException e) {
e.printStackTrace(System.out);
}
long endTime = System.currentTimeMillis();
System.out.println("耗时=" + (endTime - beginTime));
}
/**
* 单个排序的子任务
* @author yinwenjie
*/
static class MyTask extends RecursiveTask<int[]> {
private int source[];
public MyTask(int source[]) {
this.source = source;
}
/* (non-Javadoc)
* @see java.util.concurrent.RecursiveTask#compute()
*/
@Override
protected int[] compute() {
int sourceLen = source.length;
// 如果条件成立,说明任务中要进行排序的集合还不够小
if(sourceLen > 2) {
int midIndex = sourceLen / 2;
// 拆分成两个子任务
MyTask task1 = new MyTask(Arrays.copyOf(source, midIndex));
task1.fork();
MyTask task2 = new MyTask(Arrays.copyOfRange(source, midIndex , sourceLen));
task2.fork();
// 将两个有序的数组,合并成一个有序的数组
int result1[] = task1.join();
int result2[] = task2.join();
int mer[] = joinInts(result1 , result2);
return mer;
}
// 否则说明集合中只有一个或者两个元素,可以进行这两个元素的比较排序了
else {
// 如果条件成立,说明数组中只有一个元素,或者是数组中的元素都已经排列好位置了
if(sourceLen == 1
|| source[0] <= source[1]) {
return source;
} else {
int targetp[] = new int[sourceLen];
targetp[0] = source[1];
targetp[1] = source[0];
return targetp;
}
}
}
private int[] joinInts(int array1[] , int array2[]) {
// 和上文中出现的代码一致
}
}
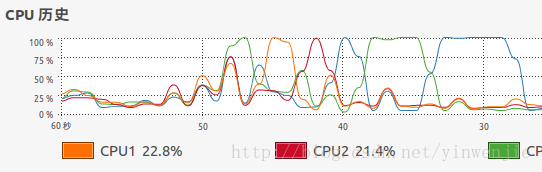
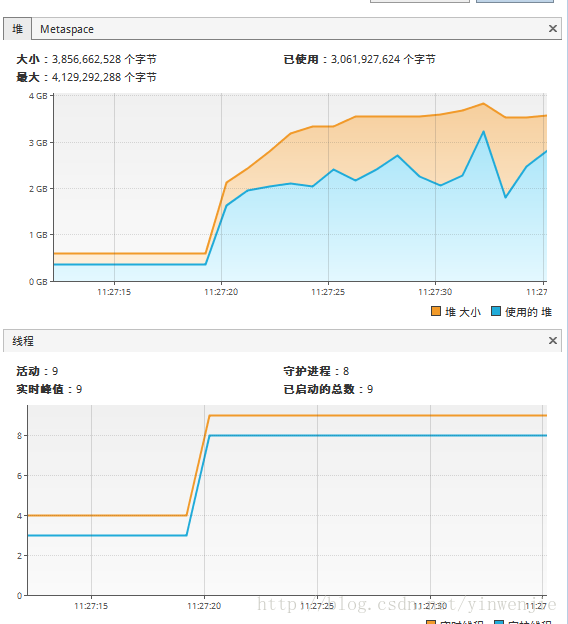
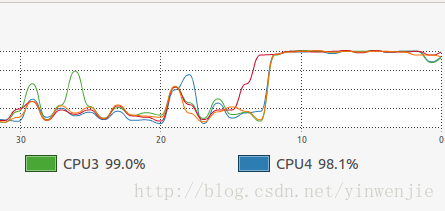
}使用Fork/Join框架优化后,同样执行1亿条随机数的排序处理时间大约在14秒左右,当然这还和待排序集合本身的凌乱程度、CPU性能等有关系。但总体上这样的方式比不使用Fork/Join框架的归并排序算法在性能上有30%左右的性能提升。以下为执行时观察到的CPU状态和线程状态:
JMX中的内存、线程状态:
CPU使用情况:
除了归并算法代码实现内部可优化的细节处,使用Fork/Join框架后,我们基本上在保证操作系统线程规模的情况下,将每一个CPU内核的运算资源同时发挥了出来。