dp线性&&LIS

1.单调栈

相关：

给定序列a[]，最少用多少个上升子序列列可以覆盖它？
答案等于a[]的最上不上升子序列的长度

给定序列a[]，最少修改多少个位置可以令其变成上升序列
解法：令a_[i] = a[i] - i，对 a_[i] 求最长上升子序列，可以得到最多有多少个位置保持不变
a[ ]1 5 3 2 7
a_[ ]0 3 0 -2 2

对于相邻两个合法的点x,y;设其中间有k个空隙
y-x-1=k
a[y]-a[x]>k
a[y]-a[x]>=k+1
即a[y]-a[x]>=y-x
整理a[y]-y>=a[x]-x

2.LIS

O(n^2)朴素

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn = 103,INF=0x7f7f7f7f;
int a[maxn],f[maxn];
int n,ans=-INF;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) 
    {
        scanf("%d",&a[i]);
        f[i]=1;
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<i;j++)
            if(a[j]<a[i]) f[i]=max(f[i],f[j]+1);
    for(int i=1;i<=n;i++) 
        ans=max(ans,f[i]);
    printf("%d
",ans);
    return 0;
}

O(nlogn) 二分插入（贪心）

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=200001;
int a[MAXN],f[MAXN];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    f[1]=a[1];
    int len=1;
    for(int i=2;i<=n;i++)
    {
        if(a[i]>f[len])
            f[++len]=a[i];
        else{
            int j=lower_bound(f+1,f+len+1,a[i])-f;
            f[j]=a[i]; 
        }
    }
    printf("%d
",len);    
    return 0;
}

树状数组维护最大值

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn =103,INF=0x7f7f7f7f;
struct Node{
    int val,num;
}z[maxn]; 
int T[maxn];
int n;
bool cmp(Node a,Node b)
{
    return a.val==b.val?a.num<b.num:a.val<b.val;
}
void modify(int x,int y)//把val[x]替换为val[x]和y中较大的数 
{
    for(;x<=n;x+=x&(-x)) T[x]=max(T[x],y);
}
int query(int x)//返回val[1]~val[x]中的最大值 
{
    int res=-INF;
    for(;x;x-=x&(-x)) res=max(res,T[x]);
    return res;
}
int main()
{
    int ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&z[i].val);
        z[i].num=i;//记住val[i]的编号，有点类似于离散化的处理，但没有去重 
    }
    sort(z+1,z+n+1,cmp);//以权值为第一关键字从小到大排序 
    for(int i=1;i<=n;i++)//按权值从小到大枚举 
    {
        int maxx=query(z[i].num);//查询编号小于等于num[i]的LIS最大长度
        modify(z[i].num,++maxx);//把长度+1，再去更新前面的LIS长度
        ans=max(ans,maxx);//更新答案
    }
    printf("%d
",ans);
    return 0;
}

例题：导弹拦截

超快写法

求一个不上升序列

求一个上升序列长度

#include<iostream>
#include<cstdio>
#include<algorithm>
#define R register
using namespace std;
const int N=100010;
int a[N],d1[N],d2[N],n;
inline bool read(int &x) {
    char c=getchar();
    if(c==EOF)return false;
    while(c>'9'||c<'0')c=getchar();
    while(c>='0'&&c<='9') {
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    }
    return true;
}
int main() {
    while(read(a[++n]));n--;
    R int len1=1,len2=1;
    d1[1]=d2[1]=a[1];
    for(R int i=2; i<=n; i++) {
        if(d1[len1]>=a[i])d1[++len1]=a[i];
        else *upper_bound(d1+1,d1+1+len1,a[i],greater<int>())=a[i];
        if(d2[len2]<a[i])d2[++len2]=a[i];
        else *lower_bound(d2+1,d2+1+len2,a[i])=a[i];
    }
    printf("%d
%d",len1,len2);
    return 0;
}

LCIS

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
#define ll long long 
#define N 3005
int f[N][N],ans;
int n,a[N],b[N];
bool v;
int maxx(int x,int y){
    return x>y?x:y;
}
int main(){
//    freopen("data.txt","r",stdin);
//    freopen("ans.txt","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)scanf("%d",&b[i]);
    for(int i=1;i<=n;i++){
        int val=0;
        if(b[0]<a[i])val=f[i-1][0];
        for(int j=1;j<=n;j++){
            if(a[i]==b[j])f[i][j]=val+1;
            else f[i][j]=f[i-1][j];
            if(b[j]<a[i])val=maxx(val,f[i-1][j]);
            ans=max(ans,f[i][j]);
        }
    }
    printf("%lld
",ans);
    return 0;
} 

拓展
1. 序列变成一个环（即a[n]和a[1] 相邻）在环上找一个最大的子段？
处理理环上问题时， 一个经典的思路路是“破环成链”
将环复制一份，即令a[i+n] = a[i]，那么环上的一段子区间，对应了序列上长度不超过n的一段区间
那么问题转化为找到一个长度不大于 n 的区间，使得 sum[r]-sum[l - 1] 最 大

可行性DP(bool,f[i][j])-->最优化DP(int,f[i]) 

有 n 个物品，若 干个询问，每个询问给定 i；问把 物品 i 去掉做背包的结果
维护 f[i] 表示前 i 个物品的背包数组，g[i] 表示后 i 个物品的背包数组，删掉 一个物品，将 f[i - 1] 和 g[i + 1] 合并即可
每次给定区间 [l, r]，问把区间 [l, r] 中的物品拿出来做背包的结果
分治, solve(l, r) 表示处理 [l, r] 的 子区间的函数
取中点 mid，预处理 f[i ~ mid] 的背包数组和 g[mid+1 ~ i] 的背包数组，回答经过 mid 的区间的询问
递归处理 (l, mid - 1) 和 (mid + 1, r)

trick

一些问题中，物品大小非常大，开不不下背包数组；另一方面，价值比较小

设 f[i] 表示要获得 i 这么多的价值， 至少要多大的背包
其实是另一个维度入手的背包
这种技巧在其它一些DP题里也会用到

第一维可以用滚动数组压掉

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define ll long long 
#define N 2005
ll f[N],ans;
ll n,a[N],b[N];
ll maxx(ll x,ll y){
    return x>y?x:y;
}
ll minn(ll x,ll y){
    return x>y?y:x;
}
ll ab(ll x,ll y){
    return x>y?x-y:y-x;
}
bool cmp(ll x,ll y){
    return x>y?1:0;
}
ll getmax(){
    sort(b+1,b+1+n);
    for(ll i=1;i<=n;i++)f[i]=ab(a[1],b[i]);
    ll v=0;
    for(ll i=1;i<=n;i++){
        v=f[1];
        for(ll j=1;j<=n;j++){
            v=min(v,f[j]);
            f[j]=v+ab(a[i],b[j]);
        }
    }
    v=f[1];
    for(ll i=1;i<=n;i++)v=minn(v,f[i]);
    return v;
}
ll getmin(){
    sort(b+1,b+1+n,cmp);
    for(ll i=1;i<=n;i++)f[i]=ab(a[1],b[i]);
    ll v=0;
    for(ll i=1;i<=n;i++){
        v=f[1];
        for(ll j=1;j<=n;j++){
            v=min(v,f[j]);
            f[j]=v+ab(a[i],b[j]);
        }
    }
    v=f[1];
    for(ll i=1;i<=n;i++)v=minn(v,f[i]);
    return v; 
}
int main(){
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)scanf("%lld",&a[i]),b[i]=a[i];
    printf("%lld
",minn( getmax(),getmin() ) );
    return 0;
}

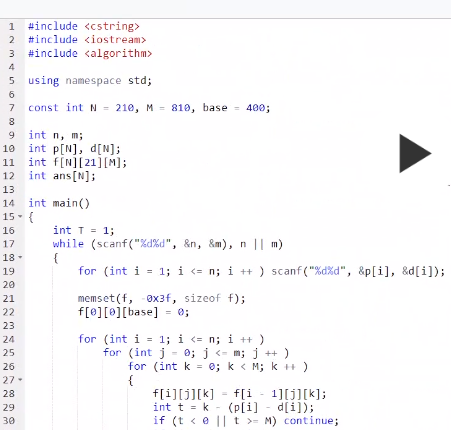
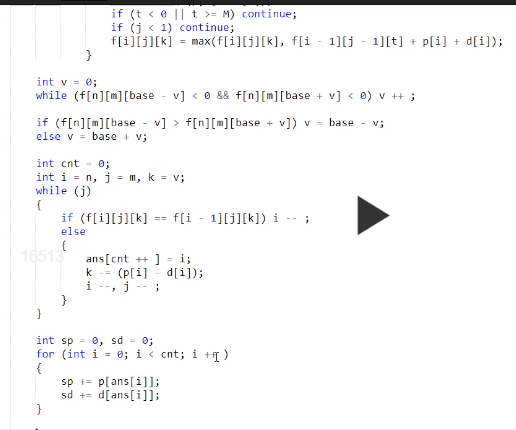
f[i][j][k]表示的是前i个人，选了j个，差值为k的 总分数最大值
转移：
1.选i f[i][j][k]=max(f[i][j][k],f[i-1][j-1][k-(p[i]-d[i]])
2.不选i f[i][j][k]=f[i-1][j][k]
可以发现i这个状态是可以 干掉的
下面是详细代码，但有些细节还没搞懂

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

int n,m,cas=1,fix,p,d,S,A,P,D;
int dp[25][805],sub[205],add[205];
vector<int> path[25][805];

int main(){
    while(~scanf("%d%d",&n,&m)){
        memset(dp,-1,sizeof(dp));
        for(int i=1;i<=m;++i)
            for(int j=0;j<805;++j)
                path[i][j].clear();
        fix=20*m;//偏移量，因为可能p[i]-d[i]为负数 
        dp[0][fix]=0;
        for(int i=1;i<=n;++i){
            scanf("%d%d",&p,&d);
            sub[i]=p-d;
            add[i]=p+d;
        }        
        for(int i=1;i<=n;++i)
            for(int j=m-1;j>=0;--j)
                for(int k=0;k<=2*fix;++k)
                    if(dp[j][k]>=0)//可以选i 
                        if(dp[j][k]+add[i]>dp[j+1][k+sub[i]]){//
                            dp[j+1][k+sub[i]]=dp[j][k]+add[i];
                            path[j+1][k+sub[i]]=path[j][k];
                            path[j+1][k+sub[i]].push_back(i);
                        }
        int kk;
        for(kk=0;kk<=fix;++kk)//枚举差值k最小的是几 
            if(dp[m][fix+kk]>=0||dp[m][fix-kk]>=0)
                break;
        S=dp[m][fix+kk]>dp[m][fix-kk]?fix+kk:fix-kk;
        A=dp[m][S];        
        P=(A+(S-fix))/2,D=(A-(S-fix))/2;
        printf("Jury #%d
",cas++);
        printf("Best jury has value %d for prosecution and value %d for defence:
",P,D);
        for(int i=0;i<m;++i)
            printf(" %d",path[m][S][i]);
        printf("

");        
    }
    return 0;
}