应用场景

概述
- Dijkstra算法 是典型单源最短路径算法,用于计算一个顶点到其他顶点的最短路径
- 单源:从一个顶点出发,Dijkstra算法 只能求一个顶点到其他点的最短距离而不能任意两顶点
- 用于无权图,或者所有边的权都相等的图,Dijkstra 算法等同于BFS搜索
- 特点:以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止
- Dijkstra算法 用于对有权图进行搜索,找出图中两点的最短距离,既不是DFS搜索,也不是BFS搜索
基本思想
- 设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组
- 第 1 组为已求出最短路径的顶点集合 (用S表示),初始时S中只有一个起点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了
- 第 2 组为其余未确定最短路径的顶点集合 (用U表示),按最短路径长度的递增次序依次把第 2 组的顶点加入S中,在加入的过程中,总保持从起点s到S中各顶点的最短路径长度不大于从起点s到U中任何顶点的最短路径长度
- 此外,每个顶点对应一个距离
- S中的顶点的距离就是从v到此顶点的最短路径长度
- U中的顶点的距离,是从v到此顶点 只包括S中的顶点为中间顶点 的当前最短路径长度
- 初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径
- 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。重复该操作,直到遍历完所有顶点
操作演示
https://blog.csdn.net/kprogram/article/details/81225176
https://zhuanlan.zhihu.com/p/40338107

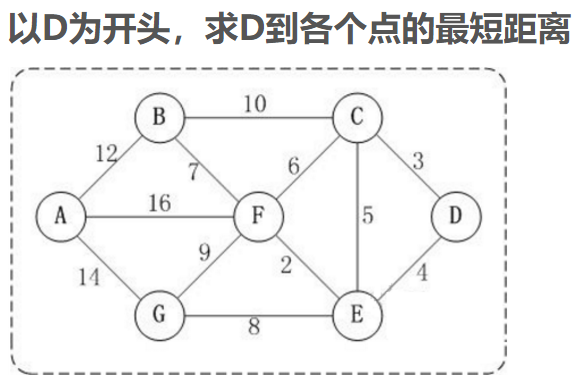

- 实际上,Dijkstra 算法是一个排序过程,就上面的例子来说,是根据D到图中其余点的最短路径长度进行排序,路径越短越先被找到,路径越长越靠后才能被找到
- 可见,要找D到A的最短路径,我们依次找到了:
- D → C 的最短路径 3
- D → E 的最短路径 4
- D → E → F 的最短路径 6
- D → E → G 的最短路径 12
- D → C → B 的最短路径 13
- D → E → F → A 的最短路径 22
代码实现
public class DijkstraAlgorithm {
public static void main(String[] args) {
char[] vertexs = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
int[][] matrix = new int[vertexs.length][vertexs.length];
final int N = 65535; // 表示不可以连接
matrix[0]=new int[]{N,5,7,N,N,N,2};
matrix[1]=new int[]{5,N,N,9,N,N,3};
matrix[2]=new int[]{7,N,N,N,8,N,N};
matrix[3]=new int[]{N,9,N,N,N,4,N};
matrix[4]=new int[]{N,N,8,N,N,5,4};
matrix[5]=new int[]{N,N,N,4,5,N,6};
matrix[6]=new int[]{2,3,N,N,4,6,N};
Graph graph = new Graph(vertexs, matrix);
graph.dijkstra(2); // C
graph.showShortestPath();
}
}
class VisitedVertex {
int[] alreadyArr; // 记录已访问顶点
int[] preVisited; // 各个顶点的前驱顶点
int[] dis; // 起点到各个顶点的距离
public VisitedVertex(int length, int index) {
alreadyArr = new int[length];
alreadyArr[index] = 1;
preVisited = new int[length];
dis = new int[length];
// 初始化 dis[]
for(int i = 0; i < length; i++)
dis[i] = 65535;
dis[index] = 0; // 出发顶点的访问距离为0
}
/**
* 判断 顶点index 是否被访问过
* @param index
* @return 如果访问过返回true; 反之false
*/
public boolean isVisited(int index) {
return alreadyArr[index] == 1;
}
/**
* 更新 出发顶点 到 顶点index 的距离为len
* @param index
* @param len
*/
public void updateDis(int index, int len) {
dis[index] = len;
}
/**
* 更新 顶点index 的前驱 为 preV
* @param index 顶点
* @param preV 顶点的前驱
*/
public void updatePreVertex(int index, int preV) {
preVisited[index] = preV;
}
/**
* 返回 出发顶点 到 顶点index 的距离
* @param index
*/
public int getDis(int index) {
return dis[index];
}
// 选择新的访问顶点
public int getVisitVertex() {
int min = 65535, index = 0;
for(int i = 0; i < alreadyArr.length; i++)
if(alreadyArr[i] == 0 && dis[i] < min) {
min = dis[i];
index = i;
}
// 设置 顶点index 为 已访问
alreadyArr[index] = 1;
return index;
}
}
class Graph {
char[] vertexs;
int[][] matrix;
VisitedVertex vv;
public Graph(char[] vertexs, int[][] matrix) {
super();
this.vertexs = vertexs;
this.matrix = matrix;
}
/**
* 求单源最短路径
* @param index 出发顶点的索引
*/
public void dijkstra(int index) {
vv = new VisitedVertex(vertexs.length, index);
update(index); // {出发顶点}
for(int j = 1; j < vertexs.length; j++) {
index = vv.getVisitVertex();
update(index); // {访问顶点}
}
}
// 更新 顶点index 到周围顶点的距离 及 周围顶点的前驱顶点
private void update(int index) {
int len = 0;
// 遍历: 顶点index 连接关系的那一行
for(int j = 0; j < matrix[index].length; j++) {
// 出发顶点 经 顶点index 到 顶点j 的距离
len = vv.getDis(index) + matrix[index][j];
if(!vv.isVisited(j) && len < vv.getDis(j)) {
vv.updatePreVertex(j, index);
vv.updateDis(j, len);
}
}
}
public void showShortestPath() {
for(int i = 0; i < vv.dis.length; i++)
System.out.printf("%c(%d) ", vertexs[i], vv.dis[i]);
}
}