1. 二叉树的问题分析
二叉树的操作效率较高,但是也存在问题, 请看下面的二叉树:
二叉树需要加载到内存的,如果二叉树的结点少,没有什么问题,但是如果二叉树的结点很多(比如 1 亿), 就存在如下问题:
- 问题1:在构建二叉树时,需要多次进行I/O操作(海量数据存在数据库或文件中),结点海量,构建二叉树时,速度有影响
- 问题2:结点海量,也会造成二叉树的高度很大,会降低操作速度
2. 多叉树
- 树家族是为了实现方便快捷的查找而存在的。树的高度是命中查找的一个不可抗拒的时间下限。在一定的数据条件下,树的高度和宽度是相互制约的。
- 对于二叉树来说,虽然易于实现,却没有实际的价值。因为二叉树的宽度固定,使树的高度无法减小,因此出现了多叉树。
- 在二叉树中,每个结点有数据项,最多有两个子结点。但如果允许每个结点可以有更多的数据项和更多的子结点,就是多叉树(Multiway Tree)。多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。
3. B树
3.1 概念
在计算机科学中,B 树(B-Tree) 是一种树状数据结构,它能够存储数据,对其进行排序并允许以 O(log n) 的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。
首先,B 树不要和二叉树混淆,在计算机科学中,B 树是一种自平衡树数据结构,它维护有序数据并允许以对数时间进行搜索,顺序访问,插入和删除。B 树是二叉搜索树的一般化,因为节点可以有 2 个以上的子节点。与其他自平衡二进制搜索树不同,B 树非常适合读取和写入相对较大的数据块(如光盘)的存储系统。它通常用于数据库和文件系统(MySQL 和 Berkeley DB 都是基于 B 树原理而建立数据库的)。
注意! B-tree 即 B树,B 即 Balanced,平衡的意思。有人把 B-tree 翻译成“B-树”,容易让人产生误解。会以为 “B-树”是一种树,而“B树”又是另一种树。实际上,B-tree 就是指的 B 树。
B 树的出现是为了弥合不同的存储级别之间的访问速度上的巨大差异,实现高效的 I/O。平衡二叉树的查找效率是非常高的,并可以通过降低树的深度来提高查找的效率。但是当数据量非常大,树的存储的元素数量是有限的,这样会导致二叉查找树结构由于树的深度过大而造成磁盘 I/O 读写过于频繁,进而导致查询效率低下。另外数据量过大会导致内存空间不够容纳平衡二叉树所有结点的情况。B树是解决这个问题的很好的结构。
B 树通过重新组织结点,降低树的高度,并且减少 I/O 读写次数来提升效率。文件系统及数据库系统的设计者利用了磁盘预读原理,将一个结点的大小设为等于一个页(页得大小通常为 4k),这样每个结点只需要一次 I/O 就可以完全载入。将树的度 M 设置为 1024,在 600 亿个元素中最多只需要 4 次 I/O 操作就可以读取到想要的元素,B(B+) 树广泛应用于文件存储系统以及数据库系统中。
3.2 定义
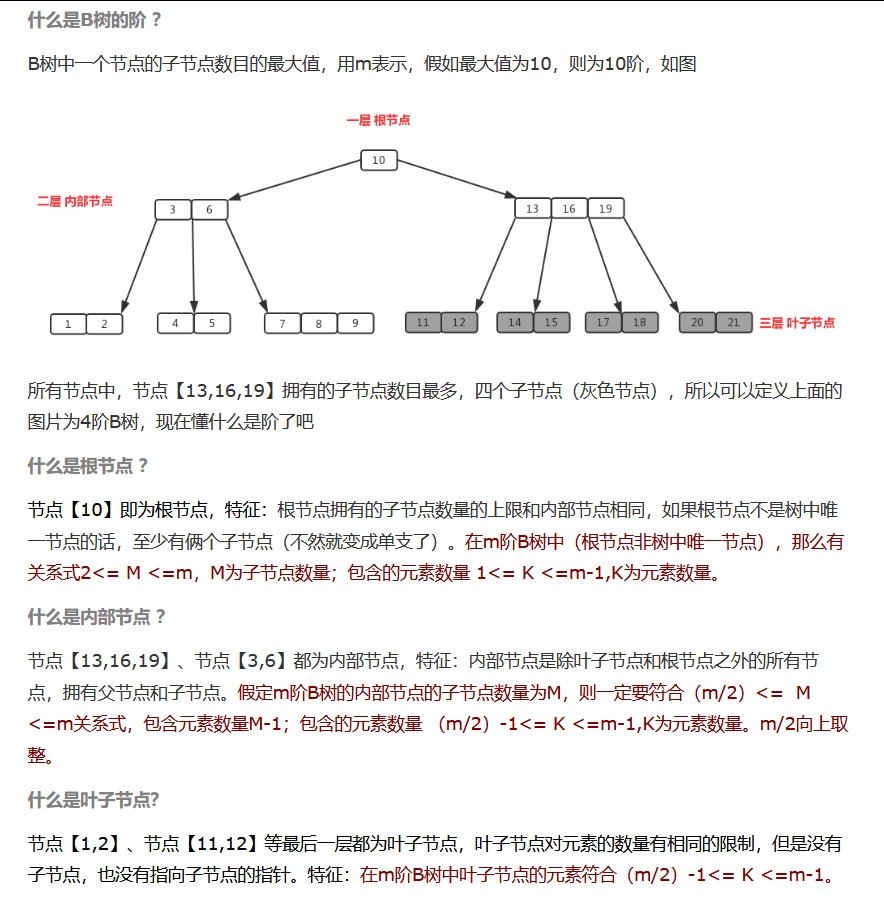
B 树是一种平衡的多分树,通常我们说 m 阶的 B 树,它必须满足如下条件:
- 每个节点最多只有 m 个子节点。
- 每个非叶子节点(除了根)具有至少 ⌈m/2⌉ 子节点。
- 如果根不是叶节点,则根至少有 2 个子节点。
- 具有 k 个子节点的非叶节点包含 k-1 个键。
- 所有叶子都出现在同一水平,没有任何信息(高度一致)。
4. 2-3查找树
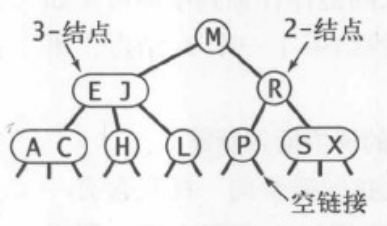
2-3 树是最简单的 B 树结构

4.1 特点
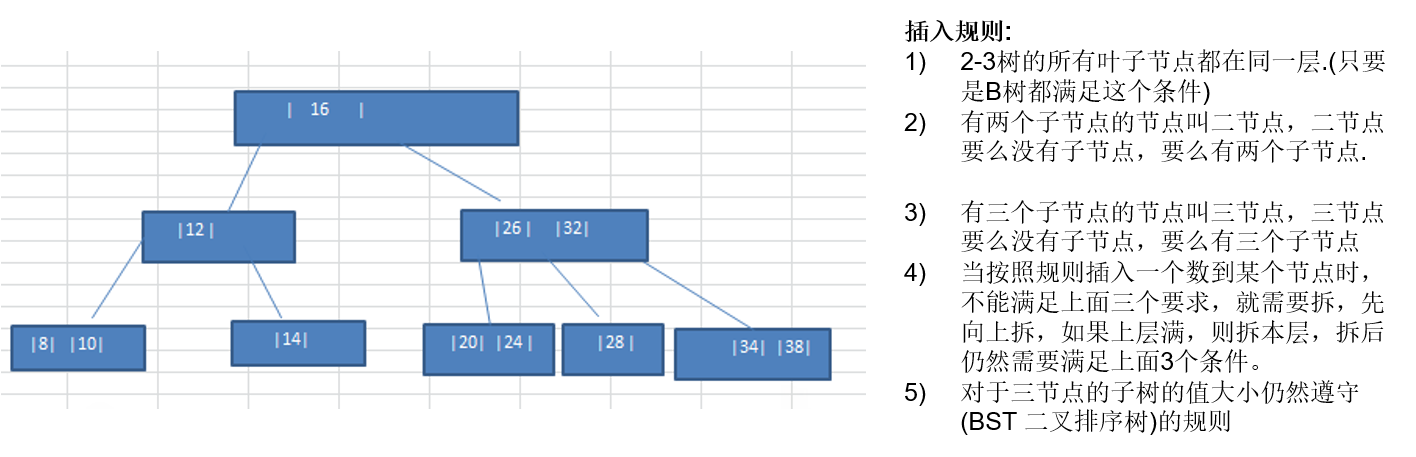
- 2-3 树的所有叶子结点都在同一层 (只要是B树都满足这个条件)
- 有 1 个 value 且有 2 个子结点的结点叫 2-结点 ,2-结点 要么没有子结点,要么有 2 个子结点
- 左子结点value < 该结点value
- 右子结点value > 该结点value
- 有 2 个 value 且 有 3 个子结点的结点叫 3-结点 ,3-结点 要么没有子结点,要么有 3 个子结点
- 左子结点value < 该结点-左侧value
- 中子结点value ∈ (该结点-左侧value, 该结点-右侧value)
- 右子结点value > 该结点-右侧value
- 2-3树是由 2-结点 和 3-结点 构成的树
4.2 查找
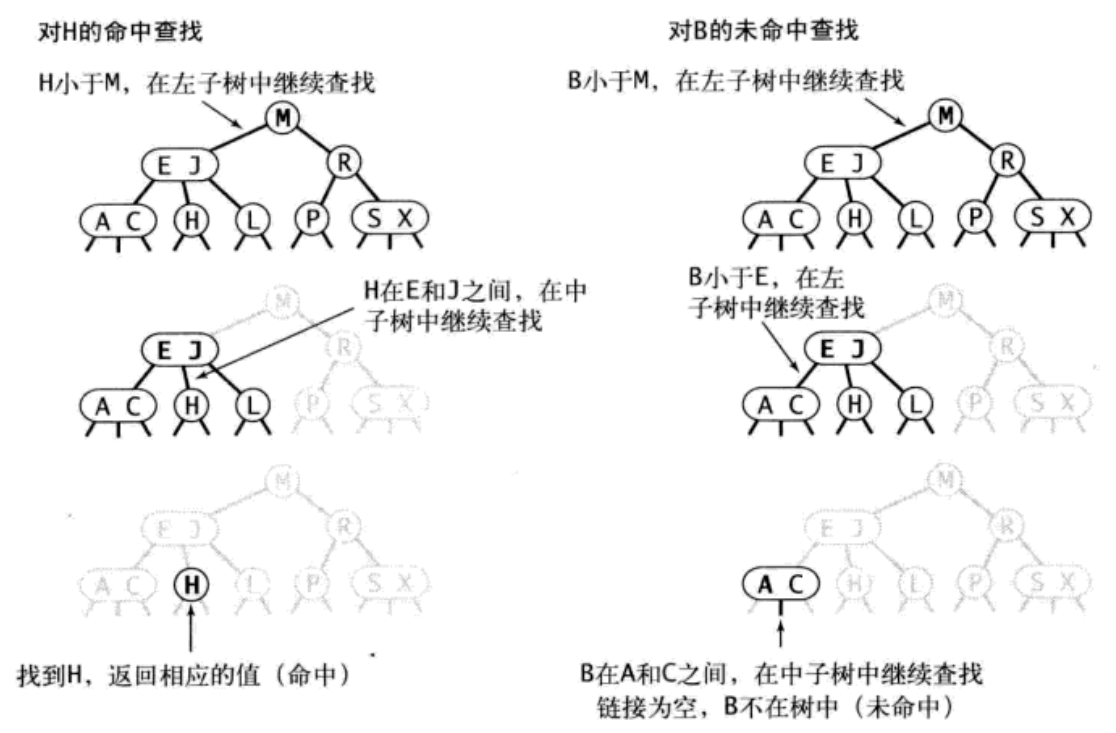
将二叉查找树的算法一般化就能得到2-3树的查找算法。要判断一个 value 是否在树中,我们先将它和根结点中的 value 进行比较。如果它和其中任意一个相等,查找命中;否则我们就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找。如果这是个空树,查找未命中。
4.3 插入原理
a. 向 2-结点中插入

b. 向一颗只含有一个 3-结点 的树中插入

c. 向一个父结点为 2-结点 的 3-结点 中插入

d. 向一个父结点为 3-结点的 3-结点中插入

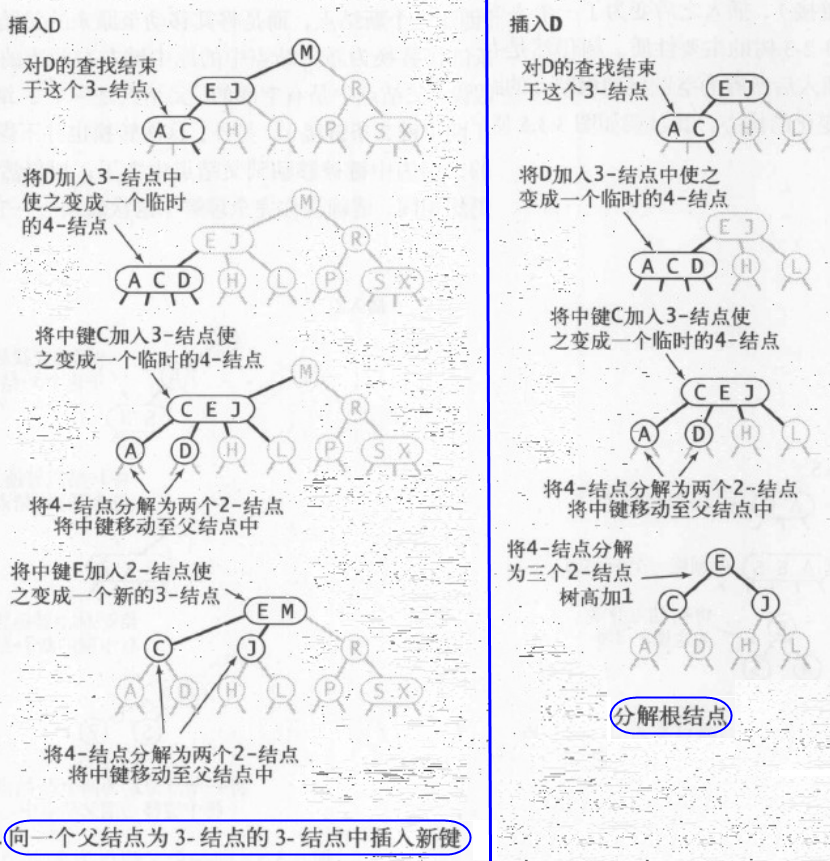
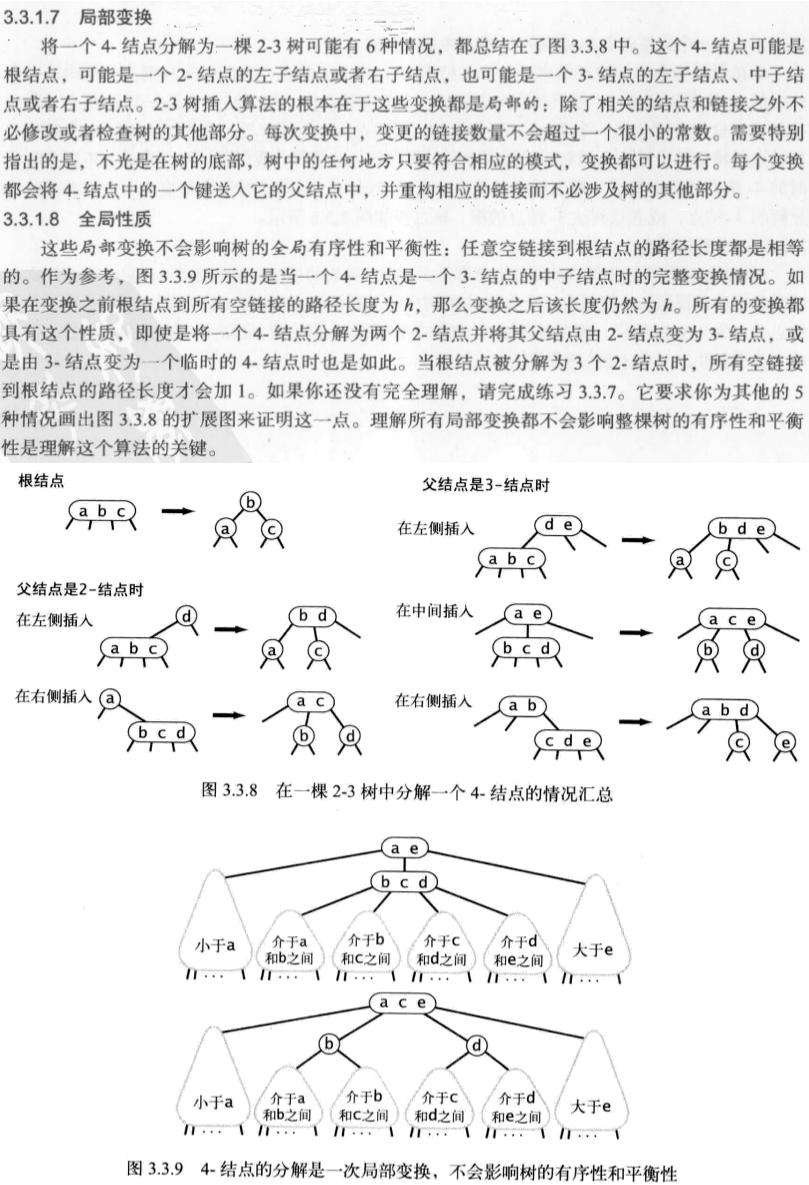
e. 局部变换和全局性质
4.4 案例
将数列 {16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成 2-3 树,并保证数据插入的大小顺序。
4.5 其他
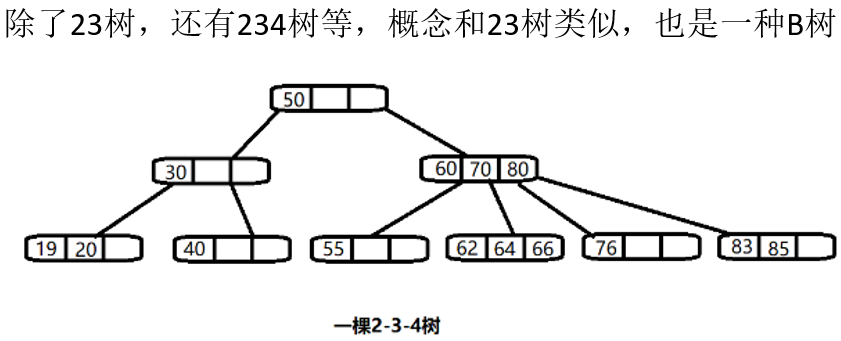
5. B树、B+树和B*树
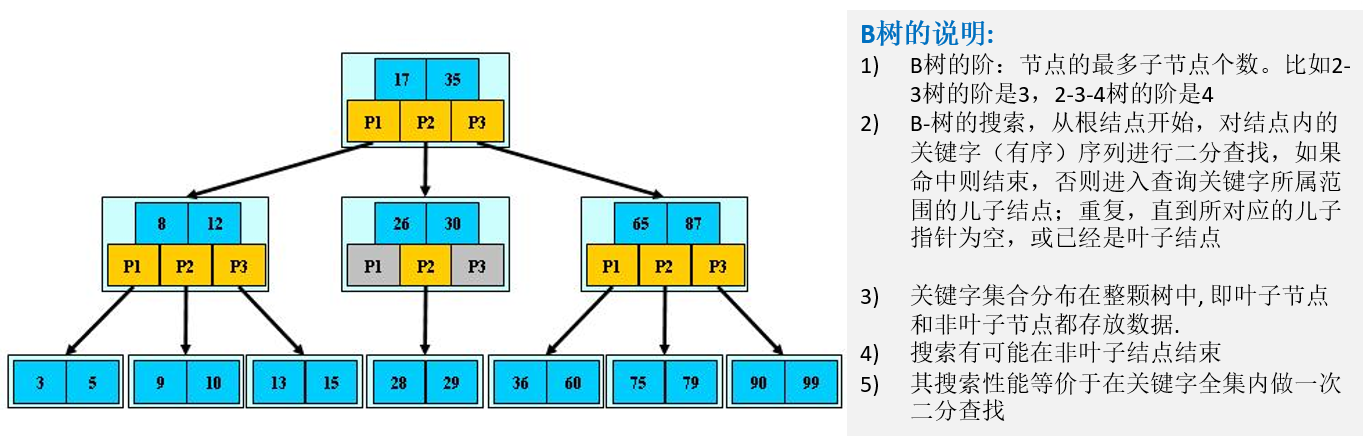
5.1 B树
B 树,概括来说是一个节点可以拥有多于 2 个子结点的二叉排序树;前面已经介绍了 2-3 树和 2-3-4 树,他们都是 B 树。
5.2 B+树
B+ 树是 B 树的变体,也是一种多路搜索树。
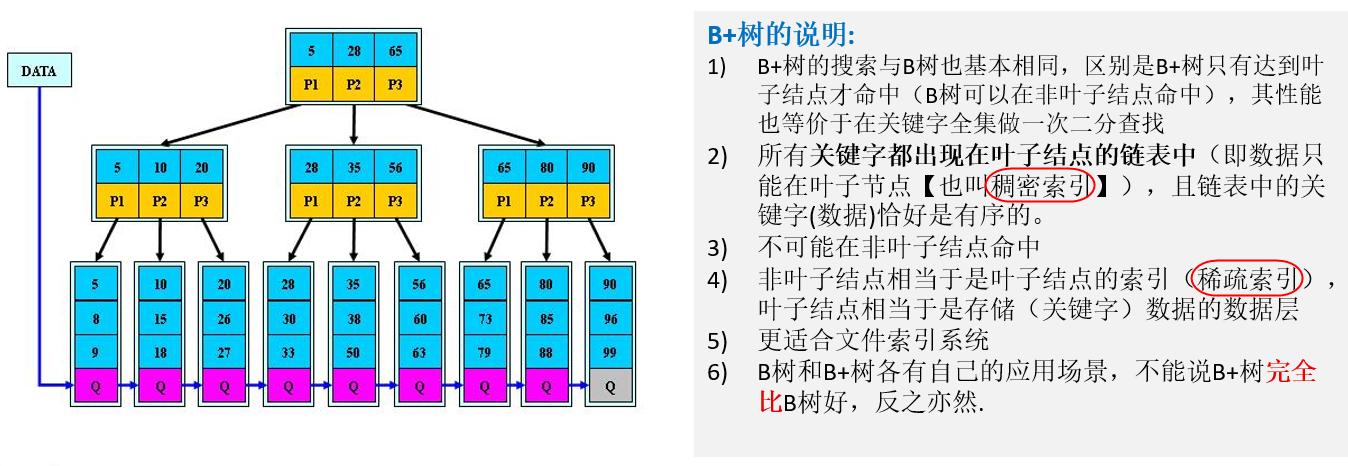
- 有 m 个子树的中间节点包含有 m 个元素(B 树中是 k-1 个元素),每个元素不保存数据,只用来索引;
- 所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接 (而 B 树的叶子节点并没有包括全部需要查找的信息);
- 所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字(而 B 树的非终节点也包含需要查找的有效信息)。
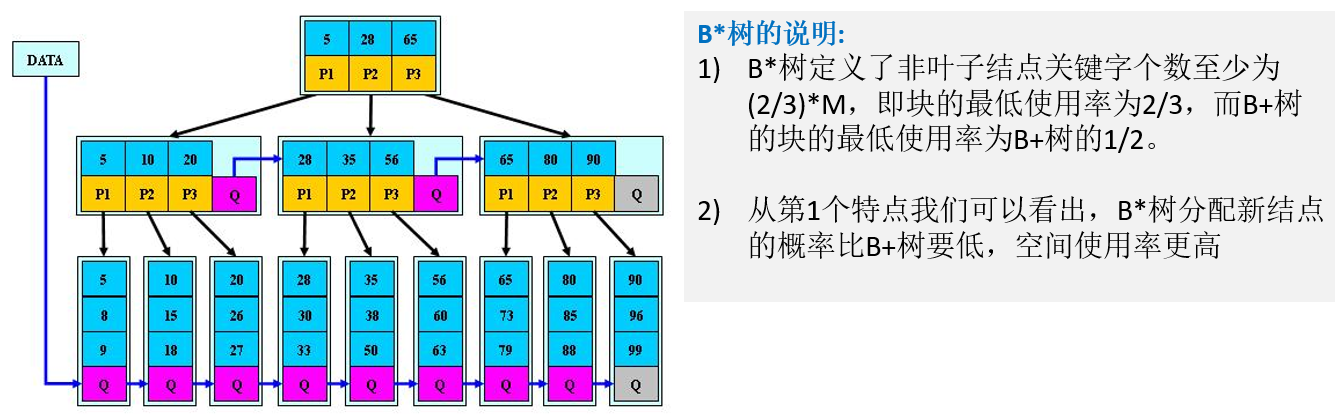
5.3 B*树
B* 树是 B+ 树的变体,在 B+ 树的非根和非叶子结点再增加指向兄弟的指针。