1. 树
1.1 定义
树是 n(n>=0) 个结点的有限集,在任意一棵非空树中:
- 有且仅有 1 个特定的称为“根”的结点。
- 当 n>1 时,其余结点可分为 m 个互不相交的有限集 T1,T2,…,Tm,其中每一个集合本身又是一棵树,并且称为根的“子树”。
1.2 基本术语
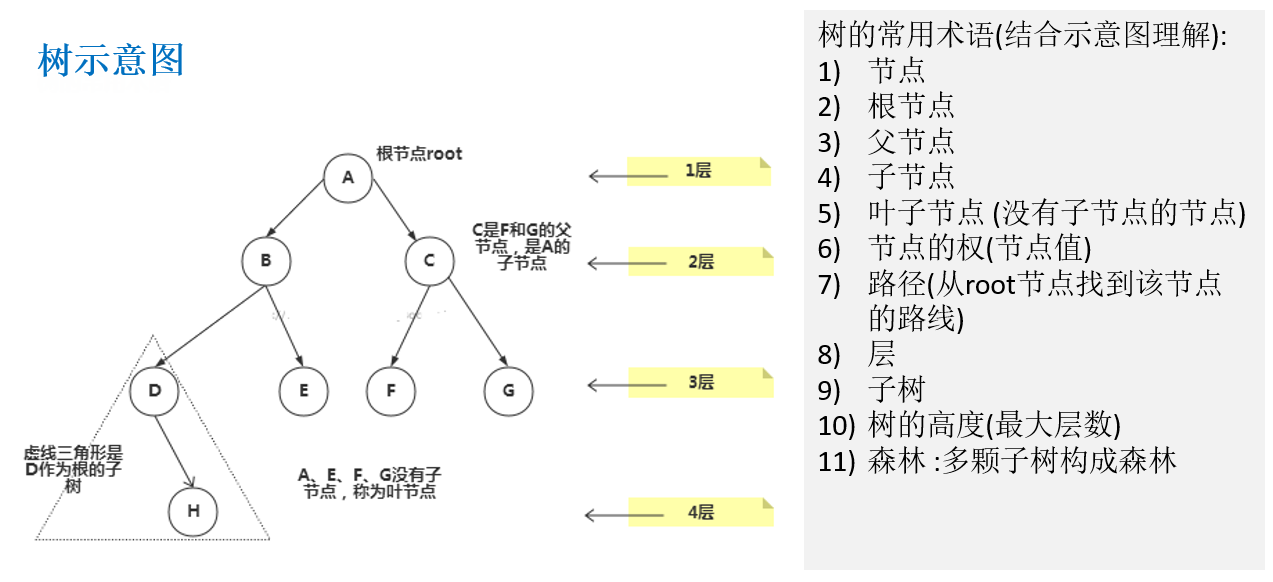
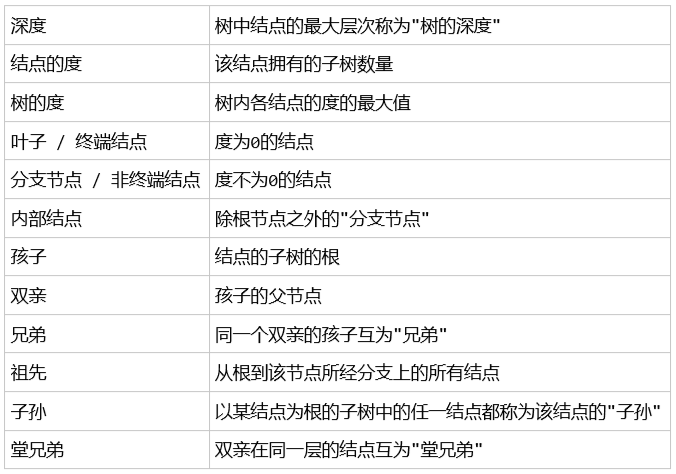
1.3 树的分类
- 【一般树】任意一个结点的子结点个数都不受限制。
- 【二叉树】任意一个结点的子结点个数最多 2 个;并且,二叉树的子树有左右之分,其次序不能任意颠倒。
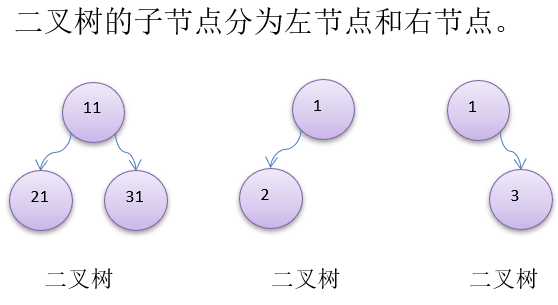
2. 二叉树
2.1 性质

2.2 分类
2.2.1 一般二叉树
2.2.2 特殊形态二叉树
- 满二叉树
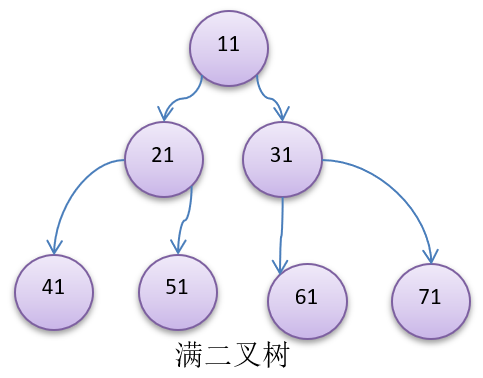
- 一棵深度为 k 且有 2^k - 1 个结点的二叉树称为“满二叉树”。
- 通俗来讲,就是在不增加树的层次的前提下,无法再多添加一个结点的二叉树称作“满二叉树”。
- 完全二叉树
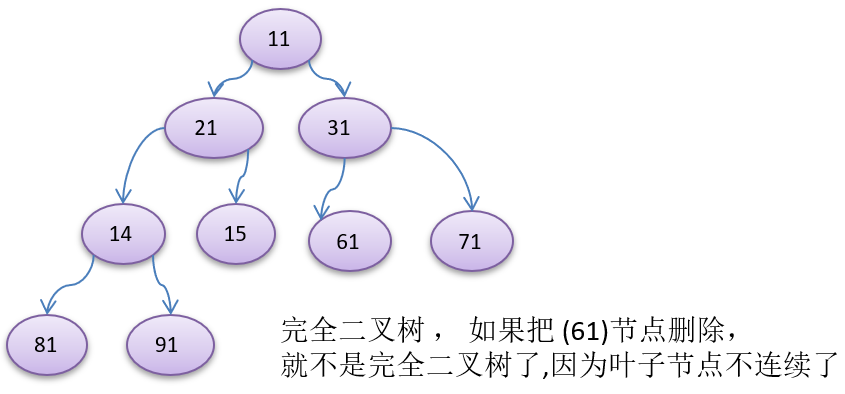
- 对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左至右,由此所引出“完全二叉树”的定义
- 深度为 k 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时,称之为“完全二叉树”。
- 通俗来讲,如果删除的是“满二叉树”最高层次最右边的连续若干结点,所剩下的二叉树就是“完全二叉树”// [满二叉树] 是 [完全二叉树] 的一个特例
- 具有 n 个结点的完全二叉树的深度为 log2n + 1