21-堆排序

1. 优先队列

• 许多应用程序都需要处理有序的元素，但不一定要求它们全部有序，或是不一定要一次就将它们排序。很多情况下我们会收集一些元素，处理当前键值最大的元素，然后再收集更多的元素，在处理当前键值最大的元素，如此这般 ...
• 在这种情况下，一个合适的数据结果应该支持两种操作：删除最大元素和插入元素。这种数据类型叫做「优先队列」。「优先队列」的使用和队列 (删除最老的元素) 以及栈 (删除最新的元素) 类似，但高效地实现它则更有挑战性。
• 之后，会学习基于二叉堆数据结构的一种「优先队列」的经典实现方式，用数组保存元素并按照一定条件排序，以实现高效地(对数级别的) 删除最大元素和插入元素操作。
• 应用场景
  • 模拟系统，其中事件的键即为发生的时间，而系统需要按照时间顺序处理所有事件
  • 任务调度，其中键值对应的优先级决定了应该首先执行哪些任务
  • 数值计算，键值代表计算错误，而我们需要按照键值指定的顺序来修正它们
  • 堆排序，通过插入一列元素然后一个个地删除其中最小/大的元素，我们可以使用「基于堆的优先队列」实现堆排序

2. 二叉堆

• 数据结构二叉堆能够很好地实现「优先队列」的基本操作。在二叉堆的数组中，每个元素都要保证大于等于另两个特定位置的元素（没有要求结点的左孩子的值和右孩子的值的大小关系）。相应的，这些位置的元素又至少要大于等于数组中另两个元素，以此类推。如果我们将所有元素画成一棵二叉树，将每个较大元素和两个较小的元素用边连接就可以很容易看出这种结构；
• 相应地，在堆有序的二叉树中，每个结点都小于等于它的父结点（如果有的话）：
  • 从任意结点向上，我们都能得到一列非递减的元素
  • 从任意结点向下，我们都能得到一列非递增的元素
  • [根结点] 是堆有序的二叉树中的最大结点
• 如果我们用指针来表示堆有序的二叉树，那么每个元素都需要 3 个指针来找到它的上下结点(父结点和两个子结点各需要一个)。但如果我们使用完全二叉树，可以先定下根结点，然后一层一层地由上向下、从左到右，在每个结点的下方连接两个更小的结点，直至将N个结点全部连接完毕。完全二叉树只用数组而不需要指针就可以表示
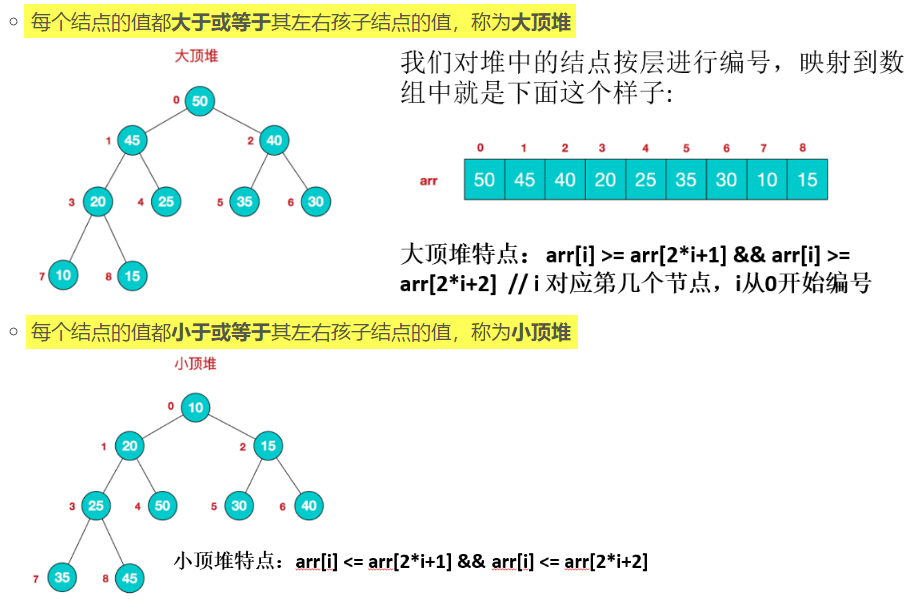
• 堆是具有以下性质的完全二叉树
  

3. 堆排序

3.1 简述

• 堆排序是利用二叉堆这种数据结构而设计的一种排序算法
  • 升序 采用 大顶堆
  • 降序 采用 小顶堆
• 堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为 O(nlogn)，也是不稳定排序

3.2 思想

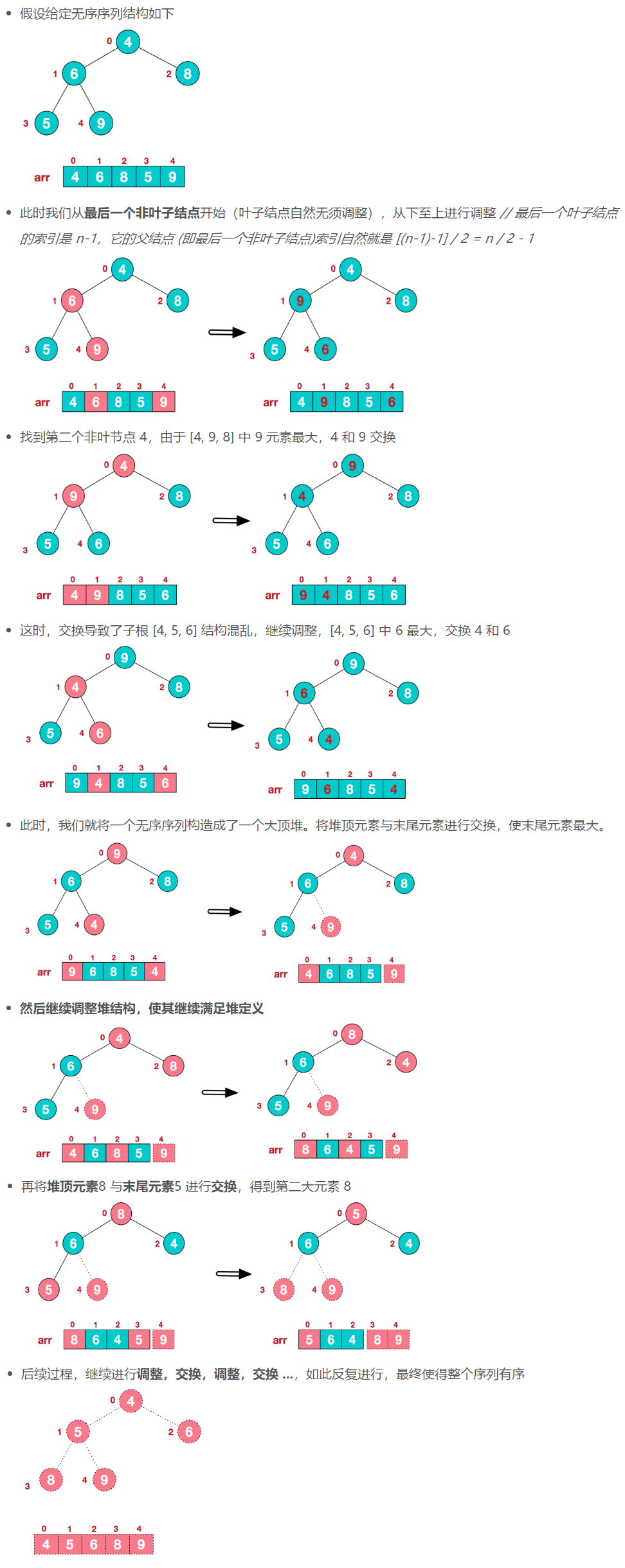
1. 将待排序序列构造成一个大顶堆 // 构建的时候是从最后一个非叶子结点开始从下往上调整
2. 此时，整个序列的最大值就是堆顶的根结点；将其与末尾元素进行交换，此时末尾就为最大值
3. 然后将剩余 n-1 个元素重新调整成一个堆，即可得到 n-1 个元素的最大值 (即 n 个元素的次大值)，再与末尾元素交换 // 调整堆是自顶向下
4. 如此反复 调整+交换，便可看到在构建大顶堆的过程中，元素的个数在逐渐减少，最后就得到一个有序序列了。

3.3 举例说明

小结：

先执行 ①，然后反复执行 ② + ③。执行 ② + ③ 之前，注意此时数组已然是个大顶堆了，所以之后 ② + ③ 所进行的反复堆调整，若调整到某一步时，父结点是大于两个儿子结点的，就可以直接 break，无需继续往下了，因为儿子之下都肯定是满足堆条件的。

1. 将无序序列构建成一个堆，根据升序/降序需求选择大顶堆或小顶堆。
2. 将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端。
3. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行〈调整+交换〉步骤，直至整个序列有序。

3.4 代码实现

public class HeapSortDemo {
    public static void main(String[] args) {
        int[] arr = {4, 2, 8, 5, 94, -6, 18, -1, 39};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void heapSort(int[] arr) {
        int temp;
        // 1. 将无序序列构建成一个堆，从最后一个非叶子结点开始，上至根结点
        for (int i = arr.length/2-1; i >= 0; i--)
            adjustHeap(arr, i, arr.length);
        // 2. 循环 {交换 + 调整}，只需给后 length-1 个元素调到对应位置上即可
        for (int j = arr.length-1; j > 0; j--) { // [length-1 → 1]
            temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;
            adjustHeap(arr, 0, j);
        }
    }

    /**
     * 将 以index结点为根的二叉树[局部二叉树] 调整为大顶堆
     * @param arr 待调整的二叉树所存放的数组
     * @param index 非叶子结点(待调整的局部二叉树的根结点) 索引
     * @param length 待调整的元素个数
     */
    public static void adjustHeap(int[] arr, int index, int length) {
        // 保存当前待调整的局部二叉树的根结点的值
        int val = arr[index];

        // 从 上 → 下 做调整
        for (int k = index*2+1; k < length; k = k*2+1) {
            // 找较大子结点
            if (k+1 < length && arr[k+1] > arr[k]) k++;
            // |—— 说明该子树满足堆要求，退出循环
            if (arr[k] <= val) break; // ∵ 当初构建堆的时候是从下至上调整的
            // |—— 说明子比父大, 故子上位
            arr[index] = arr[k];
            index = k; // 待调整二叉树的根结点索引变成其较大子结点的索引(给 val 找存放位置的过程)
        } // for 结束后, 以 {原始index} 为根的二叉树的最大值已在根的位置
        // 并且 {最终index} 保存了 {原始index} 所对应结点值 val 的最终存放位置
        arr[index] = val;
    }
}