1. 基本思想
- 归并排序(MERGE-SORT) 是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer) 策略。
- "归并"思想
- 基于归并这个简单的操作,也就是说如果想要将一个数组排序,可以先(递归地) 将它分成两半分别排序,然后将结果归并起来,即将两个有序的数组归并成一个更大的有序数组。根据这个操作所发明了一种递归排序算法 → 归并排序。
- "分治"策略
- 分治法将问题分成一些小的问题,然后递归求解
- 而治的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之
- 优缺点
- 优点:它能够保证将任意长度为 N 的数组排序所需时间和 Nlog2N 成正比
- 缺点:它所需的额外空间和 N 成正比
2. 标配
- 平均时间复杂度:O(nlogn)
- 最坏时间复杂度:O(nlogn)
- 最好时间复杂度:O(nlogn)
- 空间复杂度:O(n)
3. 举例示意
3.1 分治全过程

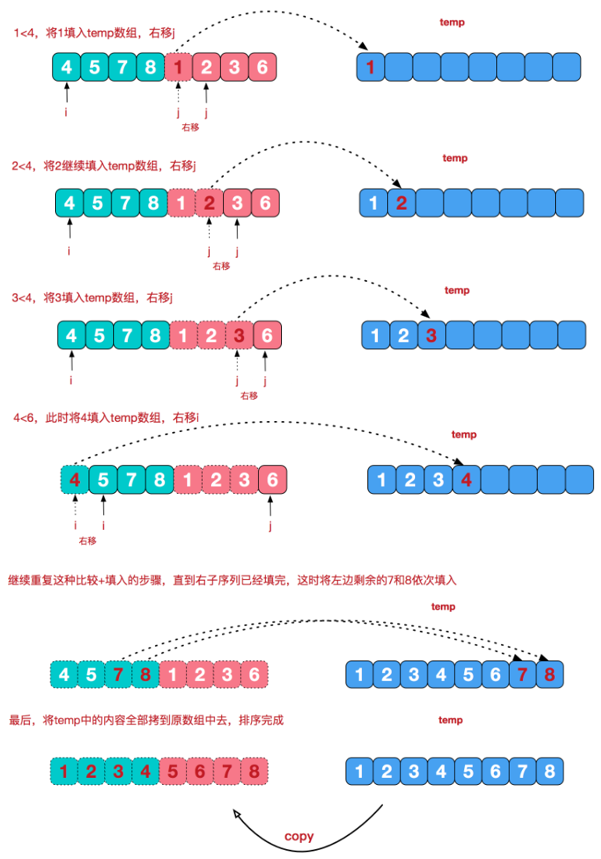
3.2 最后一次merge
要将 [4, 5, 7, 8] 和 [1, 2, 3, 6] 两个已经有序的子序列,合并为最终序列 [1, 2, 3, 4, 5, 6, 7, 8]。
4. 代码实现
public class MergeSort {
public static void main(String[] args) {
int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
int[] temp = new int[arr.length];
mergeSort(arr, 0, arr.length-1, temp);
System.out.println(Arrays.toString(arr));
}
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
// int mid = (left + right) / 2;
// 对其优化, 万一 left+right 超出表示范围了呢?
int mid = left + (right-left) >> 1;
// 向左递归继续分
mergeSort(arr, left, mid, temp);
// 向右递归继续分
mergeSort(arr, mid + 1, right, temp);
// 递归 → 从栈顶开始合并
merge(arr, left, mid, right, temp);
}
}
/**
* 对左右序列进行合并
* @param arr 待排(子)数组
* @param left 待排数组首元素索引
* @param mid 中间索引, 用来分割左右两边
* @param right 待排数组尾元素索引
* @param temp 临时存储合并后的有序序列
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 左半边有序序列的首元素索引
int j = mid + 1; // 右半边有序序列的首元素索引
int t = 0; // temp[] 的当前索引
// 1. 把左右两边(有序)的数据按照规则填充到temp中
while (i <= mid && j <= right) {
// 可得有'=', 不然成不稳定的了!
if (arr[i] <= arr[j]) temp[t++] = arr[i++];
else temp[t++] = arr[j++];
} // 直到左右两边的有序序列有一边处理完毕为止
// 用三目优化 step1 的 if-else
// temp[t++] = arr[i]<=arr[j] ? arr[i++] : arr[j++];
// 2. 把未处理完的一边的剩余数据依次全部填充到 temp 去
// a. 左边的有序序列还有剩余元素
while (i <= mid) temp[t++] = arr[i++];
// b. 右边的有序序列还有剩余元素
while (j <= right) temp[t++] = arr[j++];
/*
* 3. 把 temp[] 的元素拷贝到 arr (并不是每一次都拷贝所有元素)
* (1) left = 0, right = 1
* (2) left = 2, right = 3
* (3) left = 0, right = 3
* (4) left = 4, right = 5
* (5) left = 6, right = 7
* (6) left = 4, right = 7
* (7) left = 0, right = 7
*/
// 一定要记得 copy!
t = 0;
while (left <= right) arr[left++] = temp[t++];
}
}
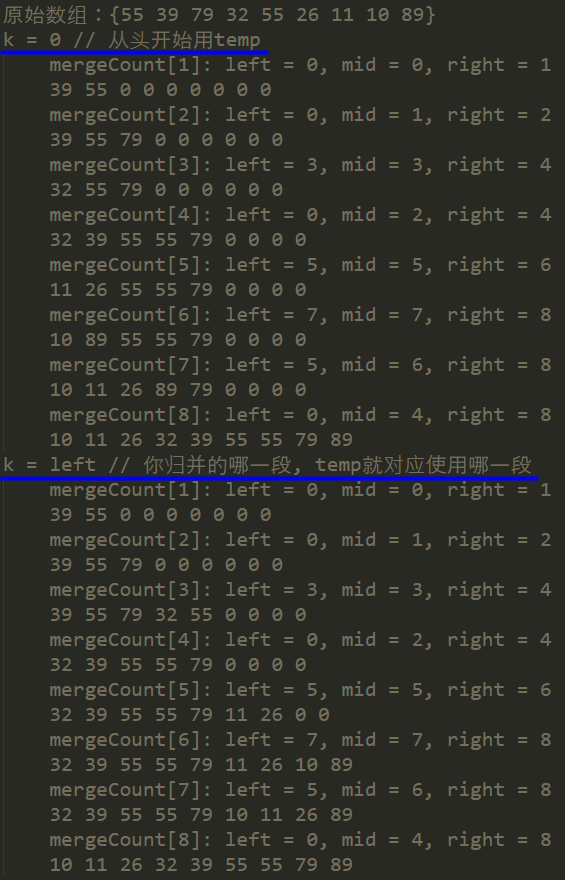
5. Tips
arr[i] <= arr[j],别把 '=' 忘了,不然就成不稳定了!- merge 完一定要记得把 temp 拷贝回 arr!
- merge 里的
t = 0 / left都行 (往回拷贝的时候记得统一!),具体区别只是在于 temp 数组是怎么被使用的~