1. 概述
- 递归就是方法在内部调用自己本身,和调别起的方法没区别
- 递归需要遵守的重要规则
- 执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
- 方法的局部变量是独立的,不会相互影响;但如果方法中使用的是引用类型变量(比如数组),就会共享该引用类型的数据
- 递归必须向退出递归的条件逼近,即该函数所处理的数据规模必须在递减,否则就是无限递归,出现 StackOverflowError
- 当一个方法执行完毕,或者遇到 return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕
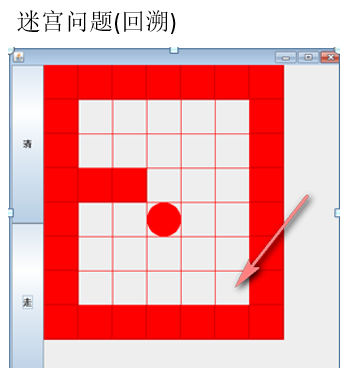
- 一个应用场景:迷宫问题(回溯)
2. 理解“方法调用”过程

- 当在一个函数运行期间,调用另一个函数时,在运行被调用函数之前,系统需要先完成 3 件事
- 将所有实参,返回地址等信息传递给被调用函数保存
- 为被调用函数的局部变量分配存储区
- 将控制转移到被调函数的入口
- 从被调用函数返回调用函数之前,系统也应完成 3 件工作
- 保存被调函数的计算结果
- 释放被调函数的数据区
- 依照被调函数保存的返回地址将控制转移到调用函数
- 当有多个函数构成嵌套调用时,按照"后调用先返回"的原则
- 上述函数之间的信息传递和控制转移必须通过"栈"来实现,即系统将整个程序运行时所需的数据空间安排在一个栈中
- 每当调用一个函数,就为它在栈顶分配一个存储区
- 每当从一个函数退出时,就释放它的存储区,则当前正运行的函数的数据区必在栈顶
- 当在一个函数运行期间,调用另一个函数时,在运行被调用函数之前,系统需要先完成 3 件事
- 将所有实参,返回地址等信息传递给被调用函数保存
- 为被调用函数的局部变量分配存储区
- 将控制转移到被调函数的入口
- 从被调用函数返回调用函数之前,系统也应完成 3 件工作
- 保存被调函数的计算结果
- 释放被调函数的数据区
- 依照被调函数保存的返回地址将控制转移到调用函数
- 当有多个函数构成嵌套调用时,按照"后调用先返回"的原则
- 上述函数之间的信息传递和控制转移必须通过"栈"来实现,即系统将整个程序运行时所需的数据空间安排在一个栈中
- 每当调用一个函数,就为它在栈顶分配一个存储区
- 每当从一个函数退出时,就释放它的存储区,则当前正运行的函数的数据区必在栈顶
3. 案例
3.1 阶乘
public static int factorial(int n) {
if (n == 1) return 1;
else return factorial(n-1) * n;
}
3.2 汉诺塔
public static void move(int dish, char x, char y) {
System.out.printf("[%d]: %c -> %c
", dish, x, y);
}
public static void hanoi(int n, char a, char b, char c) {
if (n == 1) {
move(n, a, c);
} else { // 这 [n-1个盘子] 要看作一个整体
hanoi(n-1, a, c, b); // 从a - 借助c - 到b
move(n, a, c);
hanoi(n-1, b, a, c); // 从b - 借助a - 到c
}
}
4. 递归能解决什么样的问题
使用递归解决问题的思路:[ 规模为 n 的问题 ] 的解决要借助于 [ 规模为 n-1 的问题 ] 的解决
- 各种数学问题:八皇后问题,汉诺塔,阶乘问题,迷宫问题,球和篮子的问题
- 各种算法中也会使用到递归,比如快排,归并排序,二分查找,分治算法等
- 需要用栈解决的问题 // 递归代码比较简洁