BUAA OO Unit1 Summary

BUAA OO Unit1 Summary

一.程序结构分析

第一次作业

思路：

• 这次作业较为简单，既没有非法判断，而且仅涉及幂函数因子的求导，且因子间的组合规则仅有加法，因此在这次作业中，我仅建立了一个poly类，采用了hsahmap，用幂函数的指数作为key，系数作为value，存储幂函数中的每一项，可以方便地进行化简。
• 在字符串解析部分，因为不存在空白字符非法的情况，我简单粗暴地把空白去掉之后，直接用正则表达式提取出每一项，再对每一项进行解析。
• 可能因为第一次作业比较简单，大家都比较闲，都在疯狂地追求性能极限。我除了常规地合并同类项以外，还做了一下几个工作：
  • 0项直接跳过
  • 系数为1时不输出，系数为-1时仅保留-号
  • 指数为1时不输出
  • 对项进行排序，正项先输出

总结分析

  这次作业可以说是完完全全对面向过程式设计了，责任划分不明，耦合度爆炸，连表达式解析都和MainClass类混在一块儿，丝毫没有为后面的迭代开发留下任何后路，直接导致了后面痛苦的代码重构。

UML图

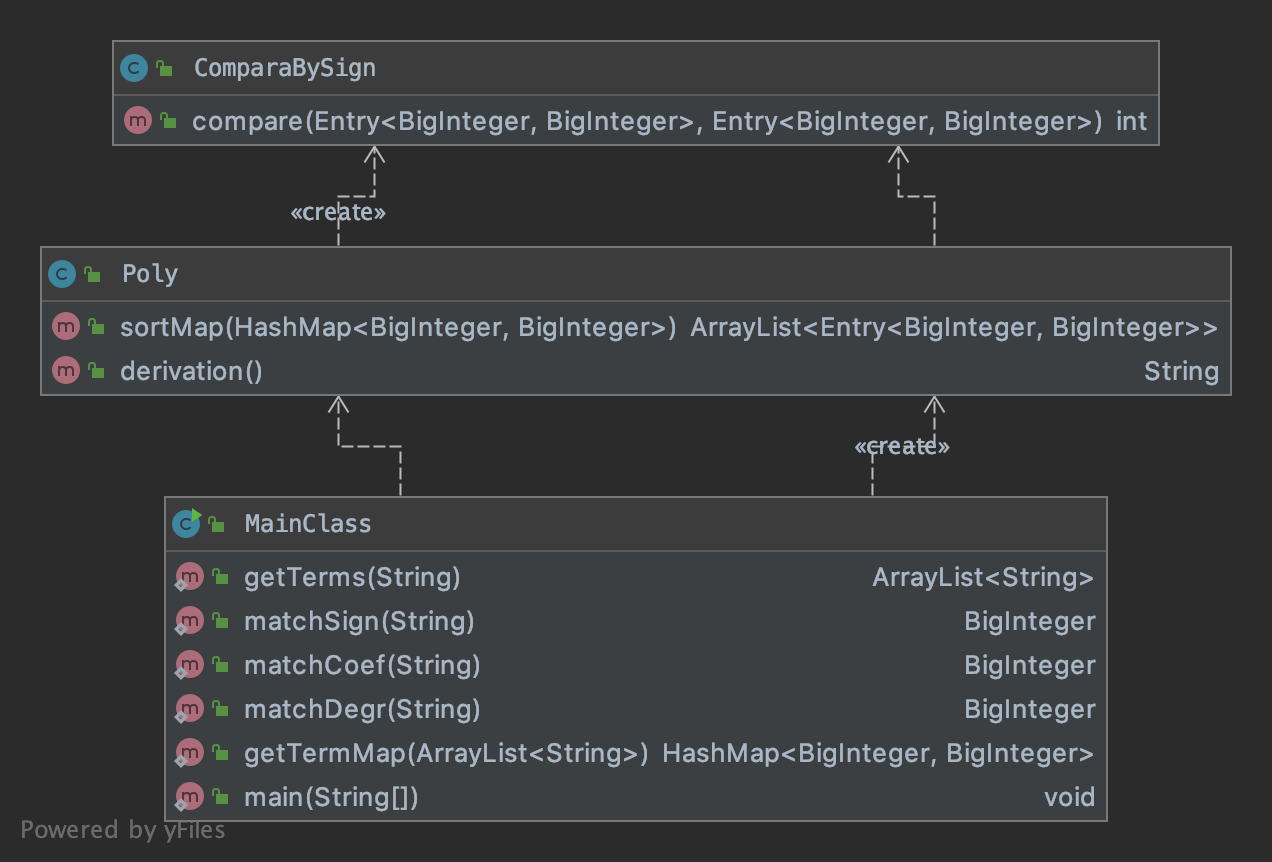
Metrics

  可以看出这次作业中我函数求导的方法比较复杂，主要原因是我求导和toString的过程其实杂糅在一起了，因此出现了复杂的if-else嵌套使用的情况，因此复杂度较高。

第二次作业

思路

• 在第二次作业中，我建立了一个Derivation的接口，对常数，幂函数，三角函数都分别建立类，对两种函数组合规则加法和乘法建立类，分别用Arraylist存储各种项和因子。所有类都继承至Derivation接口，同时都实现了接口中定义的diff和toString方法。
• 对于输入表达式解析，我建立了Parser类。直接去了空白字符后用了大正则去验证表达式的合法性。然后在表达式解析的过程中，先用toPoly的方法解析整个表达式，toPoly的方法中调用toTerm的方法解析表达式中的每一项，然后toTerm的方法调用toFactor的方法解析项中的每一个因子。

总结分析

  在看到第二次作业的指导书之后，我明白了，如果再使用面向过程的方法，只关注本次作业的要求，那么第三次作业必然重构到死。于是我痛定思痛，开始尝试一些面向对象的方法。

• 因为在表达式求导和toString中采用了接口和归一化设计的方式，因此第三次作业我在表达式存储和求导的方面仅需要在原有的基础上加入三角函数的嵌套形式即可。
• 但是在表达式解析部分依旧采用大正则直接莽，这一部分必然面临着重构。但是表达式解析中方法递归调用的思想是解决第三次嵌套因子的好方法，第三次重构这部分的时候我依然保留了这种方式。
• 这次作业比较遗憾的一点是，因为从面向过程设计到面向对象设计的转变花掉了我太多时间，再加上Arraylist的存储方式不适合化简，导致我没有去思考如何去优化。在很多同学都采用了便于合并同类项的四元组做法，并且进行了很好的三角函数化简的情况下，连同类项都没合并的我性能分惨不忍睹。不过第三次不用全部推翻重构这点还是不亏的

UML图

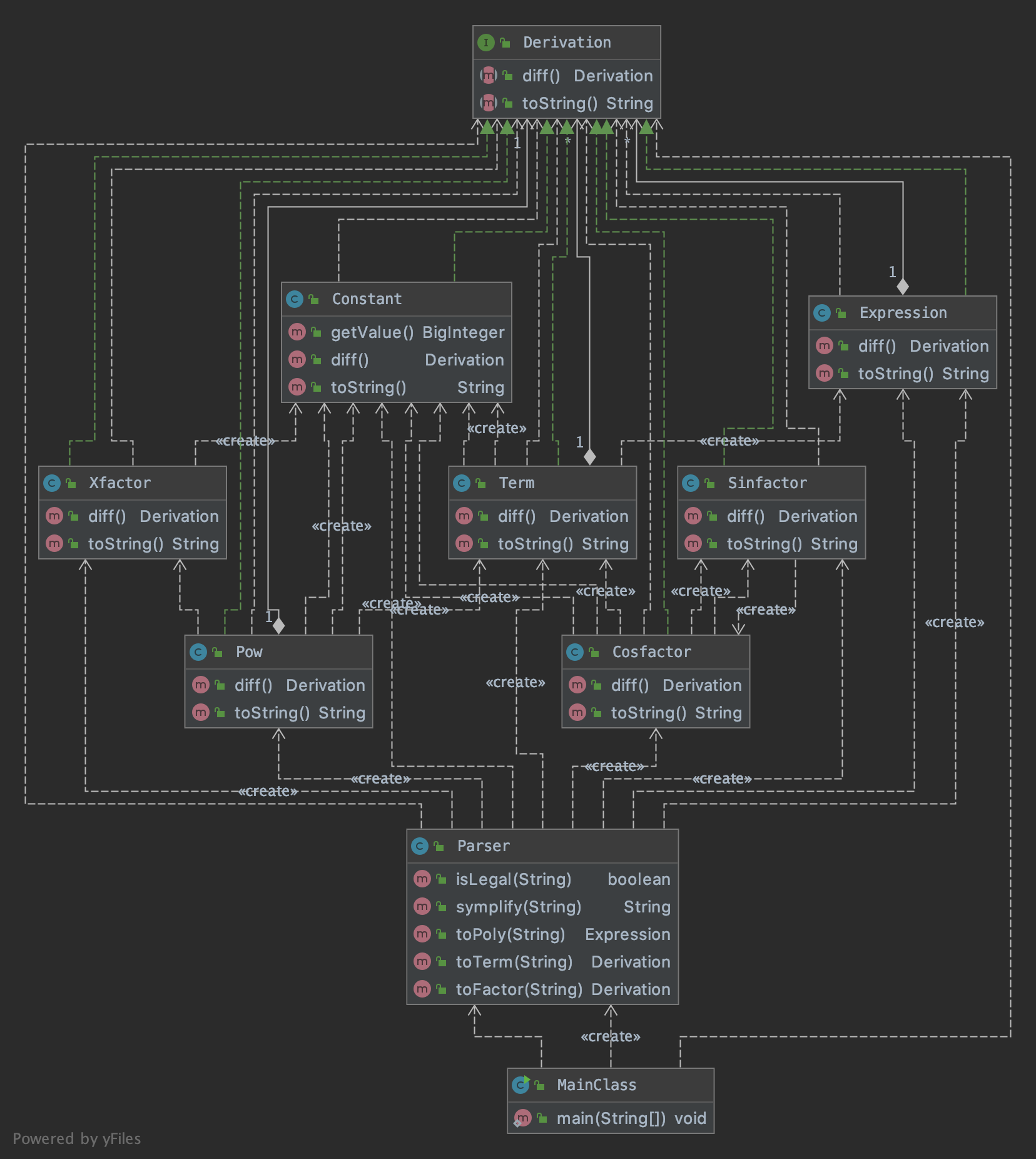
Metrics

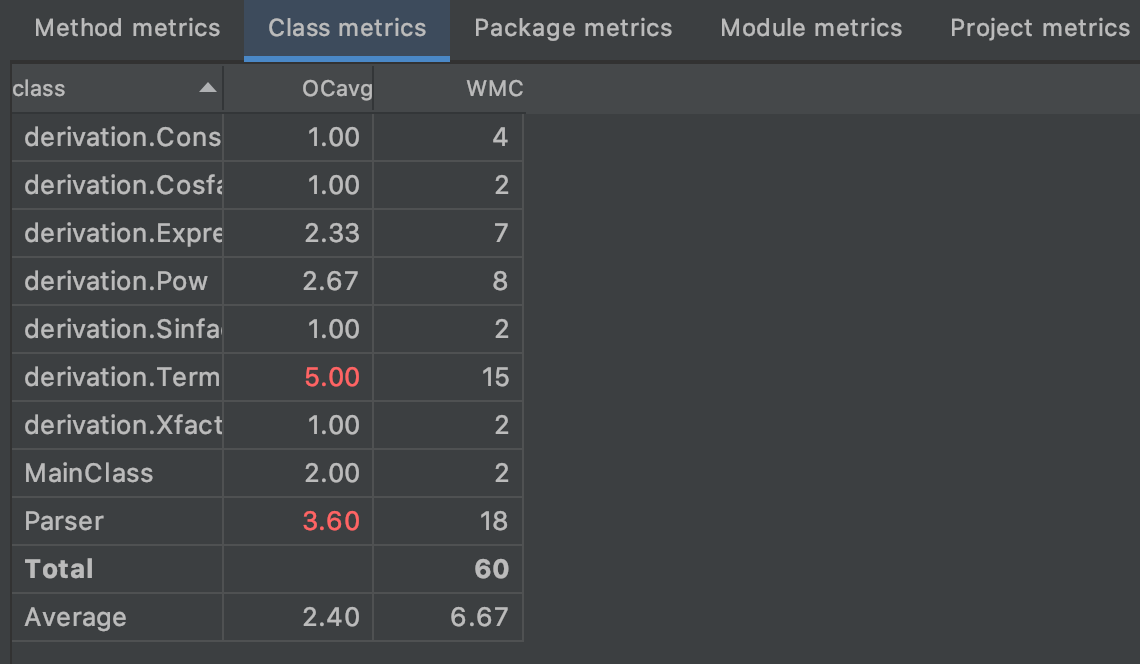
  Parser类的复杂度高在意料之中，但是Term类的复杂度也很高有点出乎我的意料，检查后发现应该是乘法求导过程中双重循环嵌套导致的。

第三次作业

思路

• 表达式的存储结构和求导方式我沿用了之前第二次的设计，并且除了在三角函数中加入嵌套因子以外，我还优化了一些存储结构，使得便于合并同类项。
  • Add类和Mult类中采用hashmap的方式存储项和因子，key值为每个项或者因子的toString方法（少数因子key值稍作改变，例如常数因子的key值为Const）。
  • Mult类中加入了一个BigInteger coef来存储系数，在往Mult类中添加因子时，如果是常数则直接与coef相乘；如果是Pow则在hashmap中寻找是否有相同的因子，如果有则调用Pow类的combine方法，将其合并；如果是Mult则将hashmap中的每一项分别加入到需要加入的Mult中；其他情况直接加入hashmap。
  • Add类的合并同类项方法类似。
• 对于输入表达式解析，我没有使用大正则的方式，而是采用了递归下降的方式，分别建立了ExprParser，TermParser和FactorParser三个类，在第二次作业的基础上加入了FactotParser类中调用FactotParser类和ExprParser类来解析嵌套因子，并且边判断非法边解析表达式，可以有效解决大正则爆栈和TLE的问题。

分析总结

  因为第二次的作业设计为第三次作业留下了一些可迭代开发的后路，所以我第三次作业的压力减轻了不少，因此留出了不少时间来思考如何进行优化。

  在优化方面，我做的最大的工作就是合并同类项，并没有针对(((x)))类似的多重括号嵌套的情况进行优化。

UML图

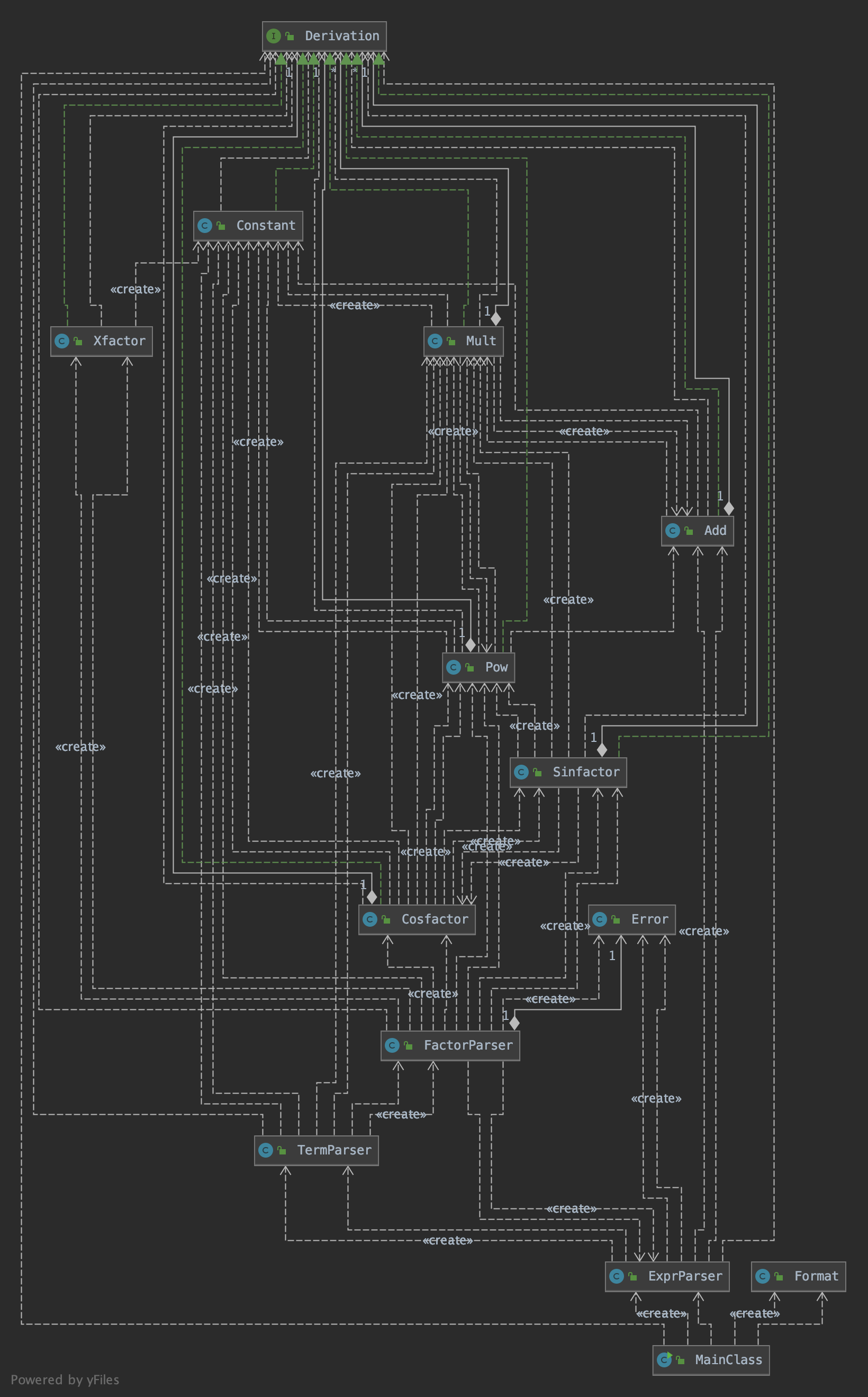
Metrics

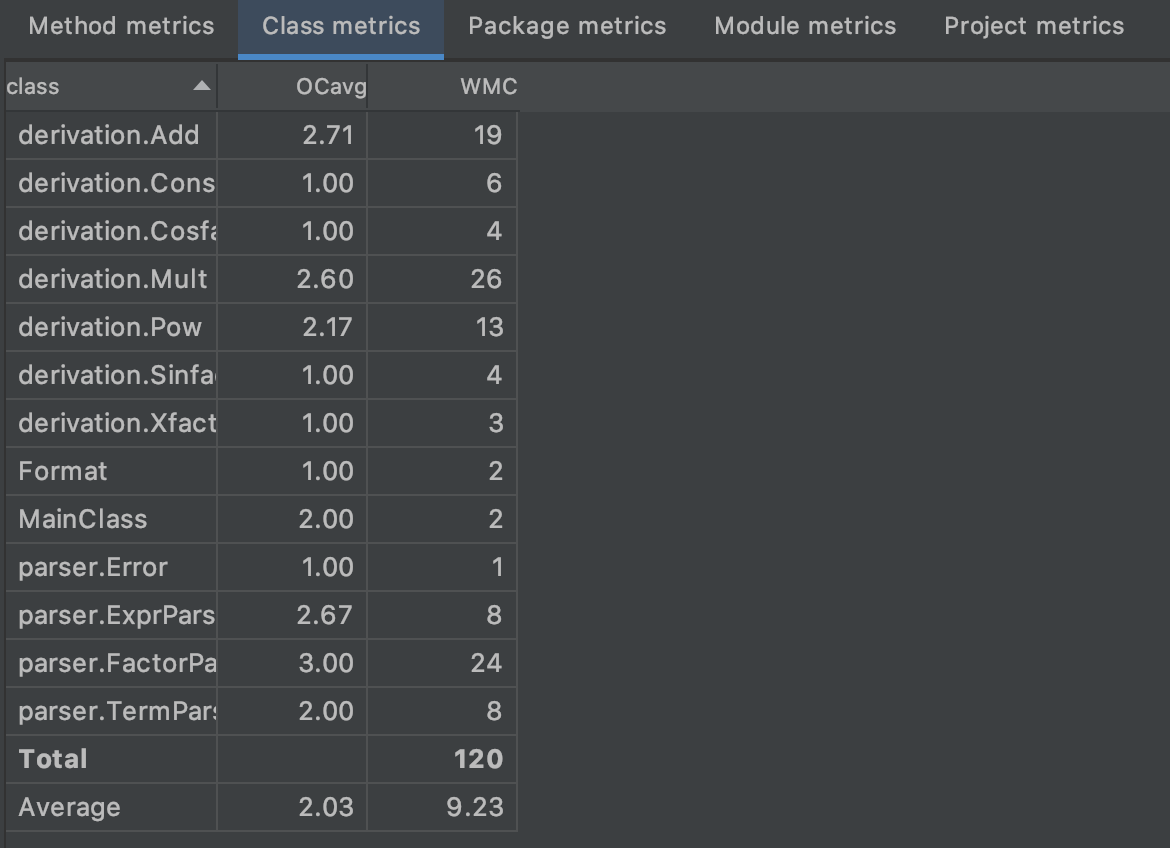
  和前两次作业的情况相比，第三次作业的复杂度情况得到了一些改善。

二.Test & Bugs

Test

  在测试方面，我采用了手写极端小数据集和评测机覆盖性测试相结合的方式。

手写极端数据

  这一部分主要是积累自己测试过程中的一些极端样例，例如第三次作业中多嵌套的情况。

评测机

  我在第一次作业的时候就尝试搭建了一个评测机，刚开始是参照讨论区大佬shell+xeger+sympy的评测机搭建方式，但是感觉并不是很好用(主要是因为我写得太菜)。

  后来在一个大佬的帮助下，get到利用subprocess.Popen()直接在python中用命令行调用.class文件的方法，使用更加方便。并且直接按指导书形式化表述生成表达式，可以解决Xeger生成字符串依赖于正则表达式的正确性的问题。

  利用形式化表述生成表达式的部分代码如下：

def generate_pow_function():
    if let_god_decide(0.3):
        return 'x'
    else:
        return 'x' + generate_whitespace() + generate_index()
      
def genetate_tri_function():
    trif = ''
    if let_god_decide(0.3):
        if let_god_decide(0.5):
            trif = "sin(" + generate_factor() + ")"
        else:
            trif = "cos(" + generate_factor() + ")"
        return trif
    else:
        if let_god_decide(0.5):
            trif = "sin(" + generate_factor() + ")"
        else:
            trif = "cos(" + generate_factor() + ")"
        return trif + generate_whitespace() + generate_index()

def generate_constant_item():
    return generate_integer()

def generate_expression_factor():
    return "(" + generate_expression() + ")"
  
def generate_factor():
    if let_god_decide(0.15):
        return generate_constant_item()
    elif let_god_decide(0.3):
        return generate_pow_function()
    elif let_god_decide(0.5):
        return generate_expression_factor()
    else:
        return genetate_tri_function()

def generate_item():
    if let_god_decide(0.3):
        return generate_item() + generate_whitespace() + "*" + generate_whitespace() + generate_factor()
    else:
        ifx = ''
        if let_god_decide(0.4):
            ifx = generate_minusplus() + generate_whitespace()
        return ifx + generate_factor()

def generate_expression():
    if let_god_decide(0.3):
        return generate_expression() + generate_minusplus() + generate_whitespace() + generate_item() + generate_whitespace()
    else:
        ifx = ''
        if let_god_decide(0.4):
            ifx = generate_minusplus() + generate_whitespace()
        return generate_whitespace() + ifx + generate_item() + generate_whitespace()

bugs

强测

  三次作业强测中都未测出bug，但是第二次作业因为没有优化的原因，性能分不高。

hacked

  第一，二次作业在互测中均未测出bug。

  第三次作业互测中被测出了一个bug。该次bug是因为我过度优化了，把多个相同表达式相乘的情况化简成了表达式的幂次，造成了format error (例如(x)*(x)*(x)我会输出为(x)**3)。而(expression)**index的形式在sympy里是合法的，所以我的评测机无法测出这种bug。这次bug的主要原因还是没有好好阅读指导书，以及自己偷懒没去手写测试样例，过度依赖评测机。

hack

  第一次作业中，大家的错误主要集中在-x**-1这个数据点上，大部分是因为优化的过程考虑不周中导致的format error。

  第二次作业中，有三个同学是因为x**-1*-1类似乘以负常数因子时，符号处理不当造成的bug。还有部分同学因为优化失误，造成了format error。

  第三次作业中，部分同学是采用了大正则导致了TLE，还有部分同学在求导过程中出现了一些失误。

三.设计模式

• 第一次作业中，采用了面向对象的设计方式，仅考虑了一次作业的要求，无法迭代开发。
• 第二，三次的作业中，实现了接口，各类因子均继承自接口，在解析输入的时候采用了递归下降的思想，创建树状结构的表达式。因此经过第二次作业重构之后，第三次作业可以在第二次作业的基础上迭代开发。

四.对比与心得体会

• 前有迭代开发，所以，接下来，代码可扩展性很有用。重构一时爽，一直重构火葬场。
• 在这次作业，学到了很多面向对象的思想。但是总的来说，在很多细节处理部分，还是运用了很多面向过程的方法，尤其解析表达式这一部分。在FactorParser中依然出现了超过六十行的方法，被迫绞尽脑汁把方法缩减到刚刚六十行以下，这依然不是一种很好的现象，说明对程序的结构和职责的划分中还有很大的问题。
• 阅读了一些同学的代码之后，我发现有不少同学采用了工厂模式。我并没有使用工厂模式，导致了我在因子解析部分的代码十分冗杂，还需要改进。
• 评测机固然好，但是过度依赖评测机而偷懒不去手写测试样例的做法是不可取的。最好的测试方法采用就是手写极端小数据集定点爆破和评测机大量随机样例测试相结合的方式。
• 善用讨论区很重要，善于向大佬学习很重要。我在第三次作业动笔前，仔细研究了第二次互测过程中发现的一份神仙代码，和HansBug助教大大在github里分享的一份往届神仙代码，对我很有启发。感谢所有帮助过我的大佬们，以及所有乐于分享的讨论区大佬们。