数制间的转换:
预备知识:
2 ^2=4 2^4=16 2^8=258 2^10=1024 ≈ 1000 =1k
2^20 ≈ 10000k =1M
2^30 ≈ 10000M
一个二进制位 :bit(比特)
8个二进制位 :Byte(字节) 1Byte=8bit
2个字节 :Word(字) 1Word=2byte=16bit
数制:
十进制:基数为10 ,逢10进1
12.34=1*10^1+2*10^0+3*10^-1+4*10^-2
二进制:基数为2 ,逢2进一
1101=1*2^3 +1*2^2+0*2^1+1*2^0=13
十六进制:基数为16,逢16进1
1001,0001,1000,0111
8 1 8 7
=9*16^3+1*16^2+8*16^1+7*16^0
八进制:基数为8,逢8进一
数制之间的转换: 二进制——>十进制 :位权相乘
十进制 ——> 二进制 :除2取余
十六进制—>十进制 :位权相乘
十进制—> 十六进制:除16取余
1. 二进制转十进制:
数字中某位的权重:2的(该位所在的位数(从右至左)-1)次方
比如:10
0的权重为:2^(1-1)=1 1的权重为:2^(2-1)=2
二进制转十进制:数字中所有位*本位的权重然后求和
比如将10101转化为十进制
10101=1*2^4+0*2^3+1*2^2+0*2^1+1*2^0=21
首先看十进制1234,这个数是什么意思?这个数我们为什么要读成一千二百三十四?因为1234=1*1000+2*100+3*10+4*1换种写法就是:1234=(1*10^3) + (2*10^2) + (3*10^1) + (4*10^0),看到了吗,有多少位,有可以拆成多少项,而每一项都是那一位上的数字乘以10的指数,这个指数个位是0,十位是1,百位是2,依次类推……
二进制也是同样的道理:比如一个二进制10101
10101=(1*2^4)+(0*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=16+4+1=21
这就是二进制转十进制
2.十进制转二进制:
- 十进制如何转二进制:将该数字不断除以2直到商为零,然后将余数由下至上依次写出,即可得到该数字的二进制表示,
以将数字21转化为二进制为例:
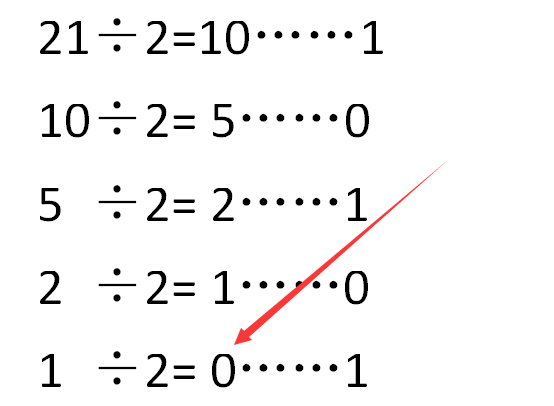
- 当商为零时,将余数由下至上依次写出,即为21的二进制表示
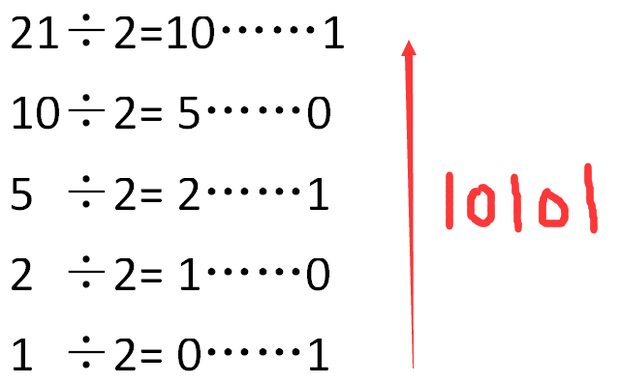
3.16进制转换:
十六进制转换有16进制每一位上可以是从小到大为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F16个大小不同的数,即逢16进1,其中用A,B,C,D,E,F(字母不区分大小写)这六个字母来分别表示10,11,12,13,14,15。
折叠16转10
16进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
例:2AF5换算成10进制:
用竖式计算:
第0位: 5 * 16^0 = 5
第1位: F * 16^1 = 240
第2位: A * 16^2= 2560
第3位: 2 * 16^3 = 8192
10997
直接计算就是:
5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997
B表示二进制,O表示八进制,D表示十进制,H表示十六进制
十进制快速转成十六进制:
用短除法。用16作除数,去除需要转换的十进制数,记下商和余数,再用16作除数,去除上一步的商,记下商和余数,……,直到商为零。
把每一步得到的余数逆序排列,就是转换成的16进制。
例如:
把256转换成16进制。
256÷16=16……0,
16÷16=1……0,
1÷16=0……1,
所以,256转换成16进制就是100。