树与数据结构——树的直径

　　　浅谈树的直径

　　树的数据结构向来是神奇且多变的,今天来谈一下树的直径

为后面更多有关树的数据结构打下基础

　　树的直径顾名思义,就是一颗树中最大路径长度,如下图

            

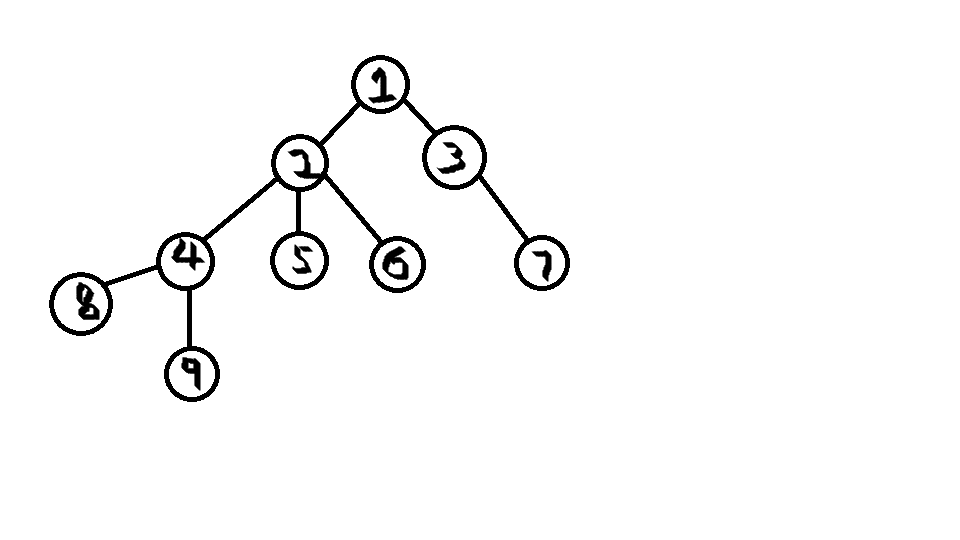
　　  如上方这个奇丑无比的树,咱们假定每两个节点之间的路径长度为1,

　　显然,他的直径应为  8或9->4->2->1->3->7,即树的直径为5

　　很好,那怎么拿代码实现呢？

　　思路:首先我们选择的算法是深搜,我们需要深搜两遍,第一遍随意找一点

深搜找到离这个点最远的点,咱们就可以确定,这个点必然是一个极点(自己定义的)

　　什么是极点什么事非极点？我们回到上图,假如我们第一次随机选点选到了2,

那非常遗憾,树的直径变为2->1->3->7,这显然不是最大的直径,我定义像2这样的点是非极点,即搜到的直径不为最大直径的点,但是！我们最后找到了7，从7我们就可以搜到最大的直径了,我们便称这样的点为极点

　　所以深搜两遍,第一遍找到极点,第二遍深搜从极点出发就可以找到树的最大直径啦~~~

代码:

#include <bits/stdc++.h>
using namespace std;
vector <int> dis[200010];
bool vis[200010];
int n,xx,yy,ans,qwq;
void dfs(int m,int deep){
    for(register int i=0;i<dis[m].size();i++){
        if(vis[dis[m][i]]) continue;
        vis[dis[m][i]]=1;
        dfs(dis[m][i],deep+1);
        vis[dis[m][i]]=0;
        if(deep>ans) qwq=m;
        ans=max(deep,ans);
    }
}
int main(){
    scanf("%d",&n);
    for(register int i=1;i<n;i++){
        scanf("%d%d",&xx,&yy);
        dis[xx].push_back(yy);
        dis[yy].push_back(xx);    
    }
    dfs(1,0);
    memset(vis,0,sizeof(vis));
    dfs(qwq,0);
    printf("%d",ans);
    return 0;
}

　　end;