深层神经网络

线性模型之局限性：

前面我们介绍了一种简单的神经网络结构。

这种模型的输出y和输入x_i满足以下关系：

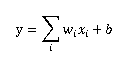
假设i=1，模型只有一个输入，x与y形成二维坐标系的一条直线。

i=n，x与y形成n+1维空间中的平面

而上次的前向传播算法可以写成：

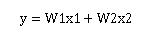也是线性模型。

而线性模型只能很好的解决线性可分的问题，（可以通过直线或者高维空间的平面）划分。非线性问题解决不了。

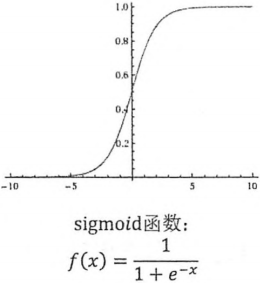
所以我们最后将激活函数设置为非线性的，比如RELU函数，这样加入非线性的元素后，就可以解决一些非线性问题。

常见激活函数：

RELU：保留>=0的值

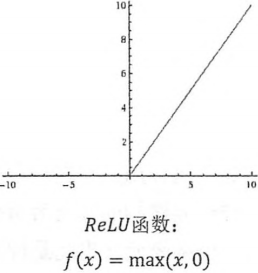
 Sigmoid：实数转成[0,1]的概率值

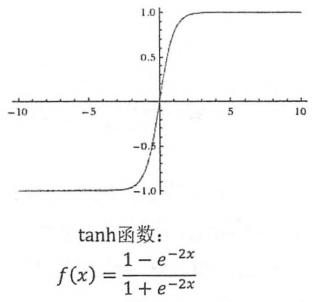
Tanh:可以把实数转成[-1,1]的概率值

 如何刻画不同神经网络的效果——————————LOSS FUNCTION

分类问题希望解决的是不同的样本分到预定好的类别中。

解决二分类问题，定义一个单输出节点的神经网络，节点输出越接近0，定义为第一类。越接近1定义为第二类。

解决多分类问题，则是定义n（类别数量）个输出节点，对于每个样例，神经网络得到一个n维数组作为输出结果。

理想情况下，如果一个样本属于类别k，那么这个类别所对应的输出节点的输出值为1，其他节点输出值为0。

以手写识别数字1~9的1为例子，神经网络模型的输出为[0,1,0,0,0,0,0,0,0]。那么如何判断一个输出向量与期望的向量有多接近呢？

交叉熵是最常用的评判方法之一。

交叉熵刻画了两个概率分布之间的距离。

通过q来表示p的交叉熵，有下列公式：,

H(p,q)=-∑_xp(x)log q(x)

而数学上，H(p,q)经过推导可以推到为

H(p,q)=H(p)+D_KL(p,q)  

D_KL(p,q) ：散度，可以用来衡量两个分布的距离。

数学上经过证明，当p=q时，H(p,q)=H(p)

当交叉熵作为神经网络的损失函数时，p代表正确答案，q代表预测值。

也就是说q与p的交叉熵值越小，两者越接近

实际应用中，为了将神经网络前向传播的结果变成概率分布,我们常常使用一层SoftMax

这样假设原始的神经网络输出为y₁,y₂,y₃,经过SoftMax回归处理之后得输出为

SoftMax(y)i=yi'=      e^yi/(e^y1+e^y2+e^y3+.....+^yn)

 上面的问题属于分类问题，再来看一下常用的回归问题：

常见的回归问题，比如说房价预测，人口预测、销量预测，这些问题与分类问题的区别是，分类问题会事先定义好一个类别，而回归问题

希望我们得到一个实数。

MSE:回归问题最常用的损失函数

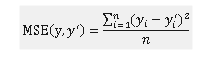
 自定义损失函数：

解决问题有时候不必拘泥于定式，针对一些具体问题，可以自己定义损失函数，使得结果更加接近实际问题的需求。

预测商品数量时，预测多了，（预测值比真实销量大），商家损失成本；预测少了（预测值比真实销量小）,损失的是商品利润。

比如我们的目标是为了得到最大化的利润，如果假设一个商品的成本是1元钱，利润是10元，少预测一个就少挣10元，多预测一个就赔1元，相当于少挣1元钱。如果使用均方误差，每个y当做销量，那么仅以销量接近真实销量是无法确保利润最大化的。

下面这个公式给出了当预测多于真实值和预测少于真实值时的损失函数：

在上面的销量预测问题中，a就等于10（正确答案多于预测答案的代价），b等于1（正确答案少于预测答案的代价）。

这样模型会更偏向于正确答案少于预测答案，也就是多预测一个。