这个系列的笔记是疫情期间在家听的网络课程——多元统计分析，由经院刘婧媛、钟威两位老师主讲，从中国大学mooc上可以搜到。笔记将对课程的主要知识点进行总结和整理，记录一些课程截图，也会从网上搜集一些相关的资料，目的是加深认识，防止遗忘。今后如果对相关内容有了更深的理解和认识，可能会对内容进行更正和补充。
本文为前两章的总结
多元统计分析是同时考量多个变量，从多元数据集中获取信息的统计方法。一个经典的例子就是鸢尾花数据集，其中的每个样本包含了四个特征和一个对应的标签，如下图所示，通过统计分析，人们可以找到鸢尾花类型（标签）与四个特征之间的关系，从而实现未来利用新数据已知的特征变量对未知的花类型进行预测的目标。
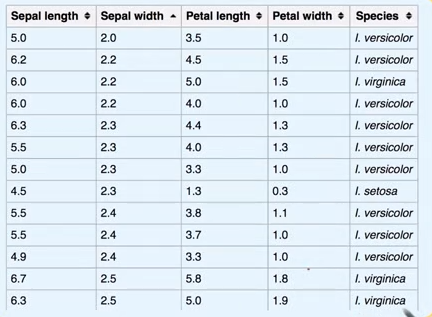
多元统计分析在市场营销、金融行业、医疗及学术研究等各个领域都有着广泛的应用。
1 随机变量数据描述
样本就是通过采样获得的部分数据点。
随机采样的样本均值可以用来估计总体均值。
样本方差是对总体方差的无偏估计。
对于多元随机向量，样本的期望是由各个分量的期望组成的向量
随机向量：由多个随机变量组成的向量。一般用来代表整个数据集对应的样本向量Y = (y1,……,yn)。
随机样本：是指总体中的每个个体都有同等的机会被选中。一般代表数据集中任意一个样本对应的特征向量。yn = (yn1,……,ynp)
对于二元随机变量，协方差等于变量乘积的均值减去变量均值的乘积
。变量间正相关则协方差cov(x,y) > 0，负相关cov(x,y) < 0，不相关则cov(x,y) = 0，此处所谓正相关负相关皆属于线性相关关系。
相关系数实际上是消除了量纲的协方差，将度量尺度标准化为[1,-1]区间，其中σ=0时说明X与Y不相关（线性独立）。
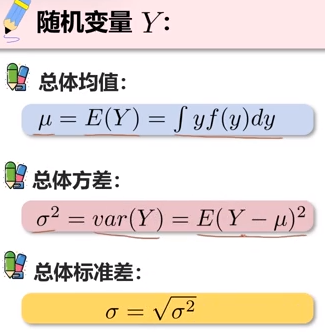
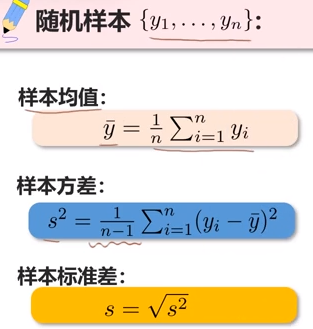
值得注意的是，σ=0时只能说明X与Y线性独立，而仍有可能以某种非线性的方式关联，但如果X和Y服从二元正态分布，并满足σ=0，则可认为是相互独立的。
为了简化数据集的处理过程，我们常将数据用矩阵的方式进行表达和计算，如n个样本、p种特征的数据集可以表示为n×p维矩阵：
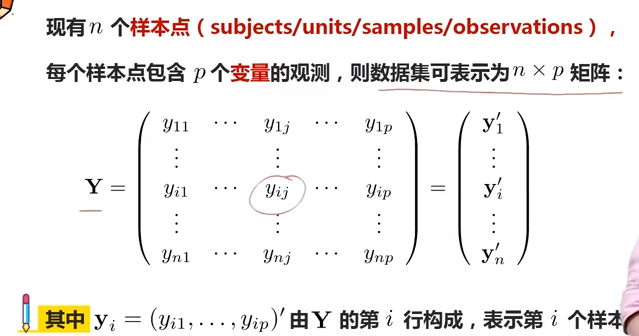
均值向量：即由随机变量的期望组成的向量。比如鸢尾花数据集中，针对随机样本而言，其均值向量就是由样本总体中各个特征的均值组成的向量，或者说其样本的期望（均值向量）是由各个分量的期望组成的向量。如上图第三张所示，多元数据的均值，由多个维度上的均值组合而成。
协方差矩阵：由各个随机变量两两之间的协方差（方差）组成。比如鸢尾花数据集中各个变量之间均可求得协方差，即可组成一个协方差矩阵。矩阵中左上到右下的对角线元素因为对应各个变量本身，因此代表方差；其他位置是两两变量之间的协方差。上图展示了针对随机向量总体的协方差矩阵Σ和针对随机样本的协方差矩阵之间的关系，个人认为可以这样理解：总体协方差矩阵是一个数据集确定的性质，是我们要获得的信息；而样本协方差矩阵是利用任意一个样本求出的，它在实际操作中作为对总体协方差的估计，其中除以n是最大似然估计，除以n-1是无偏估计，二者不相等。
协方差矩阵性质（百度百科）：
* 
* 
，其中A为矩阵，b是向量
* 
此外，协方差矩阵转化成的行列式|S|被称为广义方差（Generalized variance），如果|S|的值很小，可能是数据波动比较小，也有可能是存在共线性现象。
协方差矩阵的迹tr(S)（主对角线求和）被称为总方差，其刻画了各变量波动程度的总和，但忽略了变量间的相关性。
同理，样本相关系数矩阵也可以看做对总体相关系数矩阵的估计，主对角线作为为相同变量的相关系数，均等于1。
2 欧式距离与统计距离
协方差矩阵S的用途除了刻画数据的离散型，另外就是用于定义统计距离：
欧式距离是欧几里得空间中两点间的“直线距离”，相当于在多维空间中对两点间求距离方法的拓展。马氏距离是依据数据间协方差定义的距离，实际上是对不同方差的变量进行了归一化使其更加公平地参与比较，且与数据的测量尺度无关。当协方差矩阵为单位矩阵时，马氏距离等同于欧式距离。如上方第四张图中所示，马氏距离可看做对两个样本做标准化后求欧氏距离，y1和y2乘以协方差矩阵转置后（逆）的平方根。（一个矩阵乘以一个向量相当于对向量做了旋转和伸缩变换）新形成的两个向量自身的方差标准化为1，彼此之间协方差为0。
3 向量的分割和随机变量的线性组合
向量的分割：
以鸢尾花数据为例：
随机变量的线性组合：随机变量的线性组合往往用于将多维向量转变为一维向量。
