树、二叉树、二叉搜索树
二叉树Binary Tree
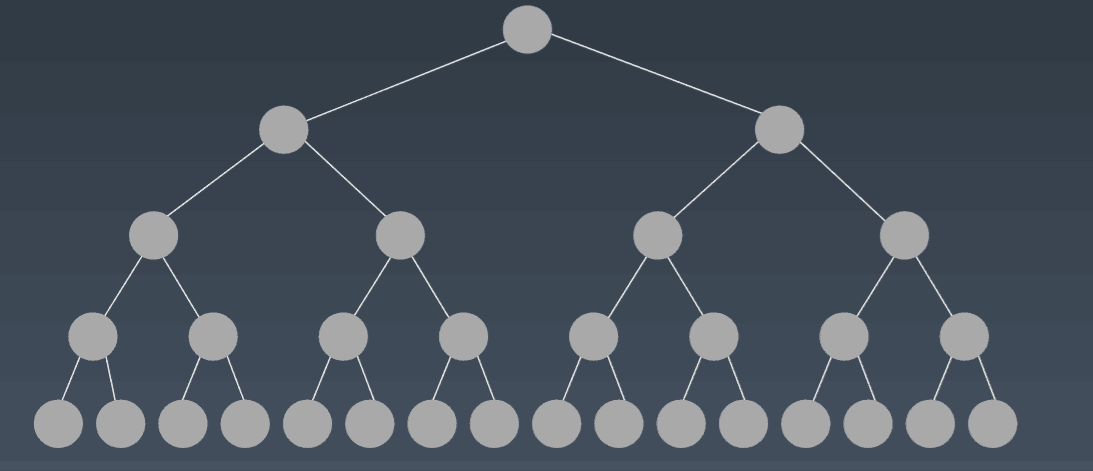
图Graph
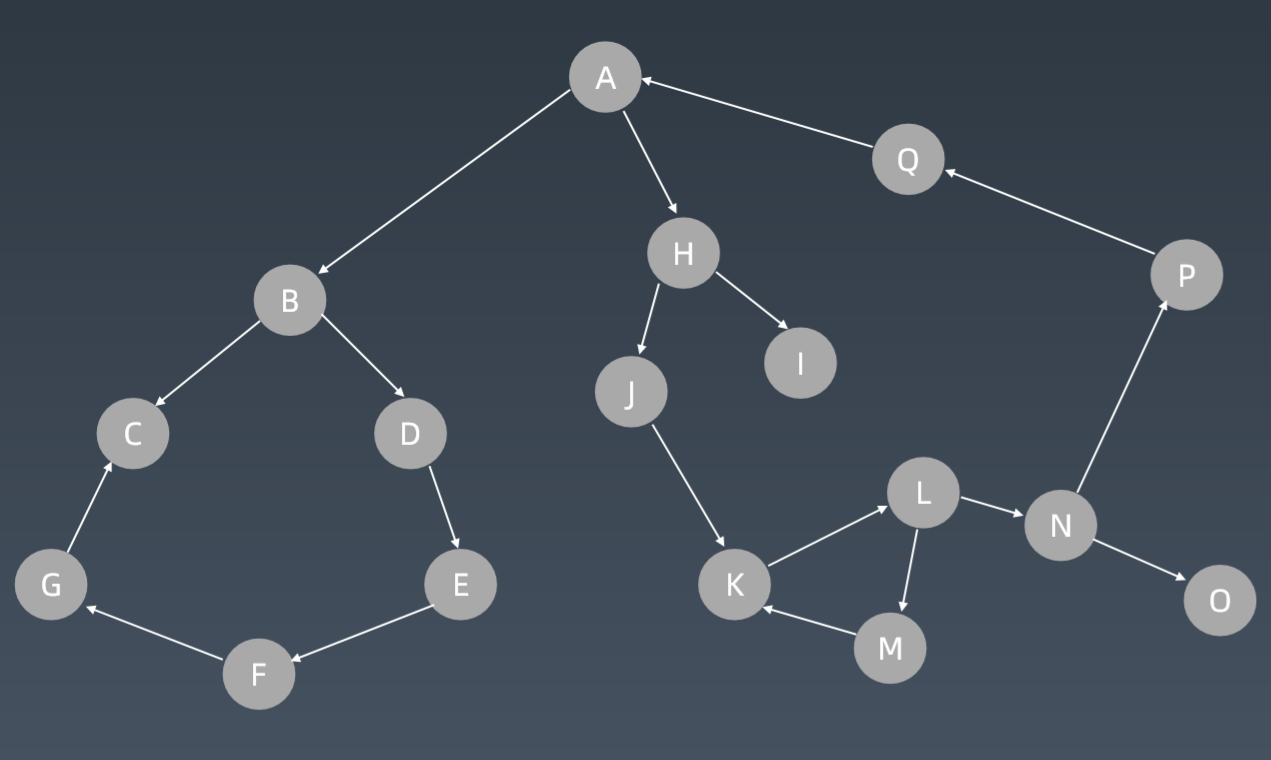
linked list是特殊化的tree tree是特殊化的graph
示例代码
class TreeNode:
def _init_(self,val)
self.val=val
self.left,self.right=None,None
struct TreeNode{
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x):val(x),left(NULL),right(NULL){}
}
public class TreeNode{
public int val;
public TreeNode left,right;
public TreeNode(int val)
{
this.val=val;
this.left=null;
this.right=null;
}
}
二叉树遍历Pre-order/In-order/Post-order
- 前序(Pre-order):根-左-右
- 中序(In-order):左-根-右
- 后序(Post-order):左-右-根
二叉搜索树Binary Search Tree
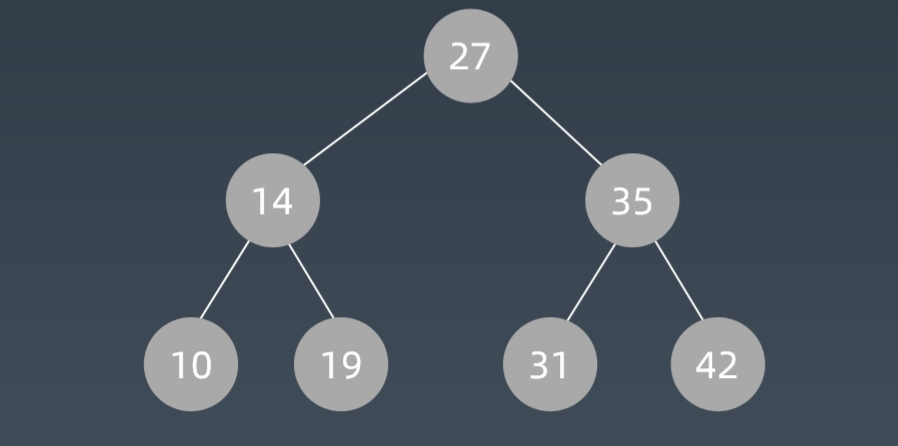
- 二叉搜索树,也称有序二叉树(Ordered Binary Tree)、排序二叉树(Sort Binary Tree),是指一颗空树或者具有下列性质的二叉树:
- 左子树上所有结点的值均小于它的根结点的值;
- 右字数上所有结点的值均大于它的根结点的值;
- 以此类推:左、右子树也分别为二叉查找树。(这就是重复性!)
中序遍历:升序排列
二叉搜索树常见操作
- 查询
- 插入新结点(创建)
- 删除
复杂度分析
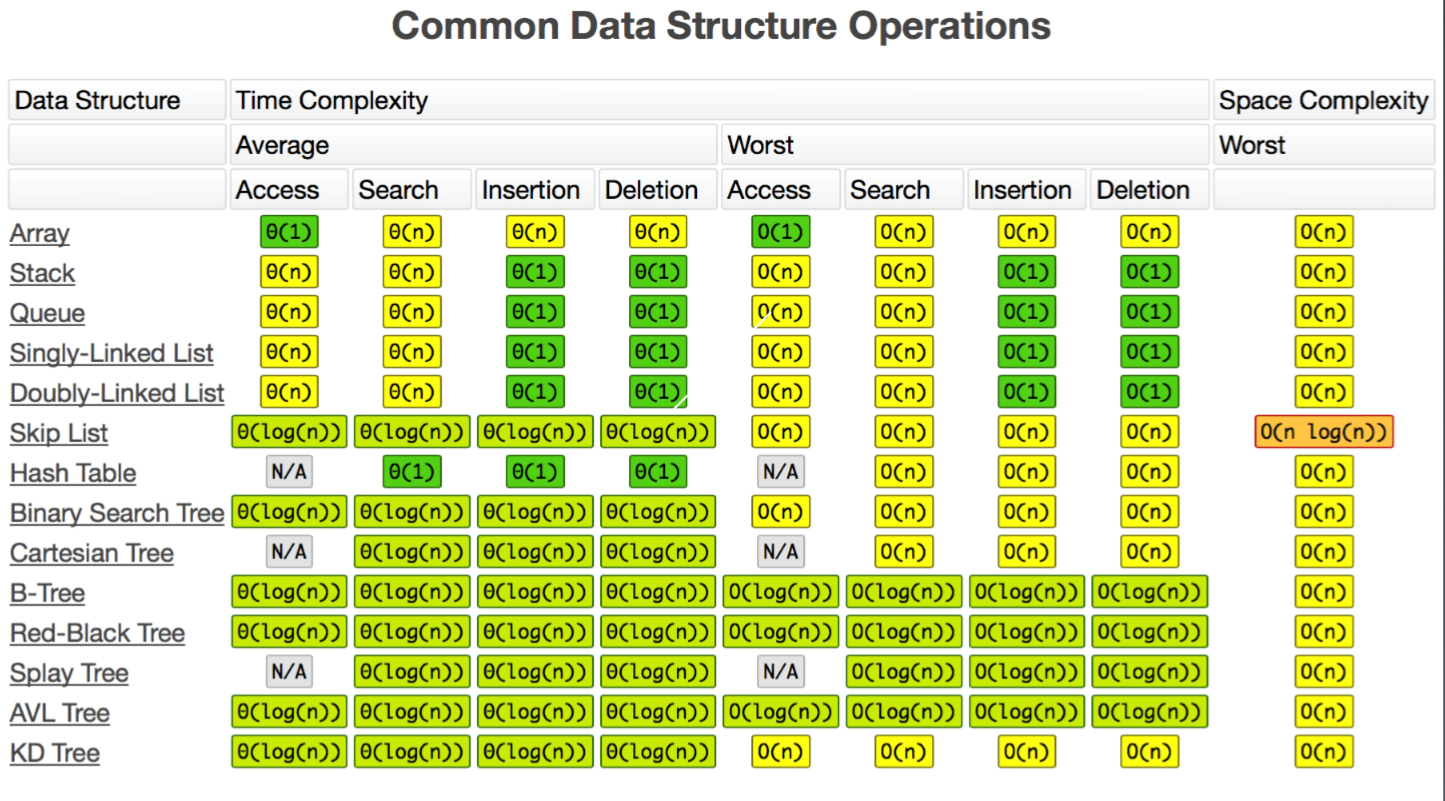
树的面试题解法一般都是递归为什么?
树的遍历LeetCode练习
lass Solution {
public:
vector<int> ans; // 答案数组
vector<TreeNode*> st; // vector 模拟栈
vector<int> inorderTraversal(TreeNode* root) {
// 特殊情况处理
if(root == NULL) return ans;
st.push_back(root);
// 对根节点实现操作 1
while(root -> left != NULL)
{
root = root -> left;
st.push_back(root);
}
while(st.size() > 0)
{
// 弹出栈顶根节点
root = st[st.size() - 1];
ans.push_back(root -> val);
st.pop_back();
// 如果当前根节点存在右节点
if(root -> right != NULL)
{
// 进入右节点
root = root -> right;
st.push_back(root);
// 重复操作 1
while(root -> left != NULL)
{
root = root -> left;
st.push_back(root);
}
}
}
return ans;
}
};
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> out;
if(!root)
return out;
vector<TreeNode*> todo;
todo.push_back(root);
while(todo.size() != 0)
{
TreeNode* n = todo.back();
out.push_back(n->val);
todo.pop_back();
if(n->right)
todo.push_back(n->right);
if(n->left)
todo.push_back(n->left);
}
return out;
}
};
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> res;
vector<Node*> nodes; nodes.push_back(root);
Node* tmp;
while(!nodes.empty()){
tmp = nodes.front(); nodes.erase(nodes.begin());
if(tmp == NULL) continue;
res.push_back(tmp->val);
nodes.insert(nodes.begin(), tmp->children.begin(), tmp->children.end());
}
return res;
}
};
lass Solution {
public:
vector<int> postorder(Node* root) {
stack <Node*> nodes;
Node* temp;
vector<int> ret;
if(root)
{
nodes.push(root);
while(!nodes.empty())
{
temp=nodes.top();
if(temp->children.size())
{
nodes.push(temp->children[0]);
temp->children.erase(temp->children.begin());
}
else
{
ret.push_back(temp->val);
nodes.pop();
}
}
}
return ret;
}
};
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
if (!root) return {};
vector<vector<int>> to_return;
to_return.push_back({root->val});
vector<int> vec;
int curr_level = 0;
queue<pair<Node*, int>> q;
q.push(make_pair(root, 0));
while (!q.empty()) {
Node* tmp = q.front().first;
int level = q.front().second;
q.pop();
if (level > curr_level) {
to_return.push_back(vec);
vec.clear();
curr_level = level;
}
for (auto n : tmp->children) {
vec.push_back(n->val);
q.push(make_pair(n, curr_level + 1));
}
}
return to_return;
}
};