前言
今天要介绍栈和队列相关算法,栈和队列这种数据结构相对简单,但是结合算法就变化莫测了,一起来看一下吧
一、栈
1、简介
栈这种数据结构可以用数组、线性表和链表等来实现,但要保证先进后出这种性质;
可能会问栈有什么应用呢?
应用非常广泛,像编辑器的撤销功能,先把“操作”入栈,然后最后入栈的,先弹出,就实现撤销功能了;
像linux内核实现的函数调用,也是把函数不断入栈,然后再弹出,还有栈和递归和密不可分的。
2、题目
LeetCode上第20号题,题目如下:
给定一个只包含字符“(”、“)”、“{”、“}”、“[”和“]”的字符串,确定输入字符串是否有效。
如果:输入字符串有效:
开括号必须用相同类型的括号括起来。
开括号必须按正确的顺序关闭。
注意,空字符串也被认为是有效的。
示例1:
输入:“()”
输出:正确
示例2:
输入:“()(){ }”
输出:正确
示例3:
输入:“(]”
输出:假
示例4:
输入:“([))”
输出:假
例5:
输入:“{[]}”
输出:正确
进行画图讲解吧,如下图: PS:依旧是全网最丑图!很努力去画,依旧很丑,看来画图的天赋了!
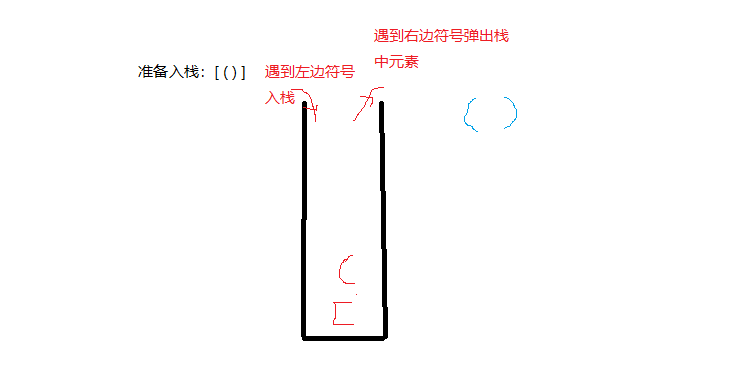
说明:
假如,[()]要入栈,规则:遇到“左边符号”入栈,“右边符号”弹出栈顶元素,进行比较,“()”符合要求,就是正确的,以此类推;还有一点要注意的,最后栈不是空的,说明栈里还有“左边符号”,这是不正确的。
3、代码及演示
代码如下:

#include <iostream> #include <stack> #include <cassert> using namespace std; // 20. Valid Parentheses // https://leetcode.com/problems/valid-parentheses/description/ // 时间复杂度: O(n) // 空间复杂度: O(n) class Solution { public: bool isValid(string s) { stack<char> stack; for( int i = 0 ; i < s.size() ; i ++ ) if( s[i] == '(' || s[i] == '{' || s[i] == '[') stack.push(s[i]); else{ if( stack.size() == 0 ) return false; char c = stack.top(); stack.pop(); char match; if( s[i] == ')' ) match = '('; else if( s[i] == ']' ) match = '['; else{ assert( s[i] == '}' ); match = '{'; } if(c != match) return false; } if( stack.size() != 0 ) return false; return true; } }; int main() { if(Solution().isValid("()")) cout << "() is valid." << endl; else cout << "() is invalid." << endl; if(Solution().isValid("()[]{}")) cout << "()[]{} is valid." << endl; else cout << "()[]{} is invalid." << endl; if(Solution().isValid("(]")) cout << "(] is valid." << endl; else cout << "(] is invalid." << endl; if(Solution().isValid("([)]")) cout << "([)] is valid." << endl; else cout << "([)] is invalid." << endl; return 0; }
我对几组数据进行了测试:()、()[]{}等,运行结果如下:

4、总结
栈的应用非常多,主要理解栈的先进后出的特性!
二、队列
1、简介
队列也是一种线性数据结构,特性是先进先出;队列有一个重要应用:广度优先遍历,相对于广度还有一种深度优先遍历,可能对于一些人还不知道广度、深度优先遍历,所以来解释一下。
对于二叉树来说:
广度优先遍历叫层序遍历更贴切,一层一层来遍历的,下面会详细讲解这种应用;
深度优先遍历就是先序、中序和后序遍历;
对图来说:就分为广度优先遍历和深度优先遍历了,图这部分之后我还会详细讲解;
2、题目
LeetCode第102题,题目如下:
给定二叉树,返回其节点值的层次顺序遍历。(例如,从左到右,逐层排列)。 例如: 给定二叉树[3,9,20,null,null,15,7], 3 / 9 20 / 15 7 返回其水平顺序遍历如下: [ [3], [9,20], [15,7] ]
这是二叉树典型的层序遍历,还有二叉树的先序、中序和后序遍历,统称为深度优先遍历!不懂的老铁可以参考这篇博客:https://www.cnblogs.com/liudw-0215/p/9835691.html,讲的很详细。
用图进行讲解吧,图如下:
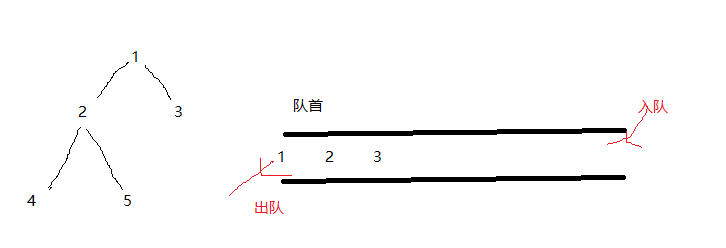
说明:先把根节点1入队,然后是2、3,以此类推,然后再出队,就可以实现层序遍历了。
3、代码实现
代码如下:

#include <iostream> #include <vector> #include <queue> #include <cassert> using namespace std; /// 102. Binary Tree Level Order Traversal /// https://leetcode.com/problems/binary-tree-level-order-traversal/description/ /// 二叉树的层序遍历 /// 时间复杂度: O(n), n为树的节点个数 /// 空间复杂度: O(n) /// Definition for a binary tree node. struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> res; if(root == NULL) return res; queue<pair<TreeNode*,int>> q; q.push(make_pair(root, 0)); while(!q.empty()){ TreeNode* node = q.front().first; int level = q.front().second; q.pop(); if(level == res.size()) res.push_back(vector<int>()); assert( level < res.size() ); res[level].push_back(node->val); if(node->left) q.push(make_pair(node->left, level + 1 )); if(node->right) q.push(make_pair(node->right, level + 1 )); } return res; } }; int main() { return 0; }
总结
栈和队列的应用非常之多,要不断理解它们的特性:先进后出、先进先出!喜欢的欢迎随时点赞,不懂的欢迎随时留言!
