前言:
先立flag吧,18年每天一个算法或数据结构知识点的学习与总结!每周5个,大约会有50个吧,感觉基础的数据结构和算法都应该掌握了!但不能每天都写博客,时间有限,每周一篇或两篇进行分享,年底进行检验结果,加油!
这次要介绍的是二分搜索树,从名字也能看出它的实现和作用了,实现是以二叉树为基础来实现的,作用是进行数据查找。
一、二分查找
二分查找应该应熟悉了吧?要在顺序储存结构中进行查找,跟最中间的数据进行比较,小的话去前半部分进行查找,否则,去后半部分去查找,其实,可以用迭代和递归分别来实现二分查找。
1、迭代法
首先,用迭代法来实现,代码如下:
// 二分查找法,在有序数组arr中,查找target // 如果找到target,返回相应的索引index // 如果没有找到target,返回-1 template<typename T> int binarySearch(T arr[], int n, T target){ // 在arr[l...r]之中查找target int l = 0, r = n-1; while( l <= r ){ //int mid = (l + r)/2; int mid = l + (r-l)/2; if( arr[mid] == target ) return mid; if( arr[mid] > target ) r = mid - 1; else l = mid + 1; } return -1; }
需要注意的一点是:int mid = (l + r)/2;我注释的这个求mid会有一个bug,当l和r达到int的最大值时,会出现越界的问题。这也是算法的魅力,需要注意很多细节并有很多地方需要优化!学无止境!
2、递归法
用递归法实现,代码如下:
// 用递归的方式写二分查找法 template<typename T> int __binarySearch2(T arr[], int l, int r, T target){ if( l > r ) return -1; int mid = (l+r)/2; if( arr[mid] == target ) return mid; else if( arr[mid] > target ) return __binarySearch2(arr, 0, mid-1, target); else return __binarySearch2(arr, mid+1, r, target); }
用递归最重要的一点就是:要有结束条件
3、main函数测试两种方法
写一个main函数,进行简单的测试,数据量用的比较大,PS:用一个算法进行一下优化,一看数据量就几百,根本没必要优化,数据量不过万,谈算法意义并不大!
main函数主要对两种算法进行时间对比:

int main() { int n = 1000000; int* a = new int[n]; for( int i = 0 ; i < n ; i ++ ) a[i] = i; // 测试非递归二分查找法 clock_t startTime = clock(); for( int i = 0 ; i < 2*n ; i ++ ){ int v = binarySearch(a, n, i); if( i < n ) assert( v == i ); else assert( v == -1 ); } clock_t endTime = clock(); cout << "Binary Search (Without Recursion): " << double(endTime - startTime) / CLOCKS_PER_SEC << " s"<<endl; // 测试递归的二分查找法 startTime = clock(); for( int i = 0 ; i < 2*n ; i ++ ){ int v = binarySearch2(a, n, i); if( i < n ) assert( v == i ); else assert( v == -1 ); } endTime = clock(); cout << "Binary Search (Recursion): " << double(endTime - startTime) / CLOCKS_PER_SEC << " s"<<endl; delete[] a; return 0; }
运行结果如下:
会发现递归运行时间长,因为递归会反复调用,会耗时的。
二、二分搜索树
1、介绍
什么是二叉搜索树呢?
首先,它是一颗二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
如下图就是二叉搜索树:
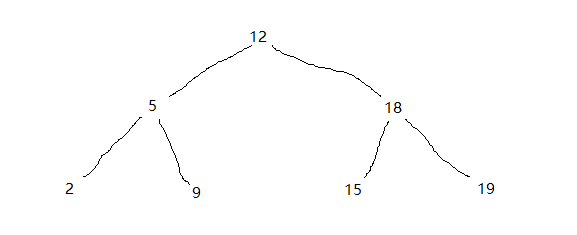
2、构建一个BST类
先建一个BST类用于存放二叉搜索树,还包括一些构造函数、插入和查找等,代码如下:

template <typename Key, typename Value> class BST { private: struct Node { Key key; Value value; //key和value值相等 Node *left; //左子树 Node *right; //右子树 //结构体的构造函数 Node(Key key, Value value) { this->key = key; this->value = value; this->left = this->right = NULL; } Node(Node *node) { this->key = node->key; this->value = node->value; this->left = node->left; this->right = node->right; } }; Node *root; int count; public: BST() { //类的构造函数 root = NULL; count = 0; } ~BST() { destroy(root); } int size() { return count; } bool isEmpty() { return count == 0; } void insert(Key key, Value value) { root = insert(root, key, value); } bool contain(Key key) { //是否包含 return contain(root, key); } Value* search(Key key) { //查找 return search(root, key); } // 前序遍历 void preOrder() { preOrder(root); } // 中序遍历 void inOrder() { inOrder(root); } // 后序遍历 void postOrder() { postOrder(root); } // 层序遍历 void levelOrder() { queue<Node*> q; q.push(root); while (!q.empty()) { Node *node = q.front(); q.pop(); cout << node->key << endl; if (node->left) q.push(node->left); if (node->right) q.push(node->right); } } // 寻找最小的键值 Key minimum() { assert(count != 0); Node* minNode = minimum(root); return minNode->key; } // 寻找最大的键值 Key maximum() { assert(count != 0); Node* maxNode = maximum(root); return maxNode->key; } // 从二叉树中删除最小值所在节点 void removeMin() { if (root) root = removeMin(root); } // 从二叉树中删除最大值所在节点 void removeMax() { if (root) root = removeMax(root); } // 从二叉树中删除键值为key的节点 void remove(Key key) { root = remove(root, key); }
3、插入节点
首先,它是二叉树,都具有的性质是递归,所以用递归相对比较简单,画一张图如下供参考:

假如,先插入8,跟根节点12比较,比它小去左子树,跟节点5比较,比它大去右子树;再例如,插入13,跟根节点12比较,比它大去右子树;代码如下:
// 向以node为根的二叉搜索树中,插入节点(key, value) // 返回插入新节点后的二叉搜索树的根 Node* insert(Node *node, Key key, Value value) { if (node == NULL) { count++; return new Node(key, value); } if (key == node->key) node->value = value; else if (key < node->key) node->left = insert(node->left, key, value); else // key > node->key node->right = insert(node->right, key, value); return node; }
4、查找节点
跟插入的思想很像,也是不断比较,用递归的思想去查找,代码如下:
// 在以node为根的二叉搜索树中查找key所对应的value Value* search(Node* node, Key key) { if (node == NULL) return NULL; if (key == node->key) return &(node->value); else if (key < node->key) return search(node->left, key); else // key > node->key return search(node->right, key); }
5、三种遍历方法
三种方法分别是:先序遍历、中序遍历和后序遍历。画图讲解一下吧,如下图: PS:依旧是全网最丑图,不接受反驳!
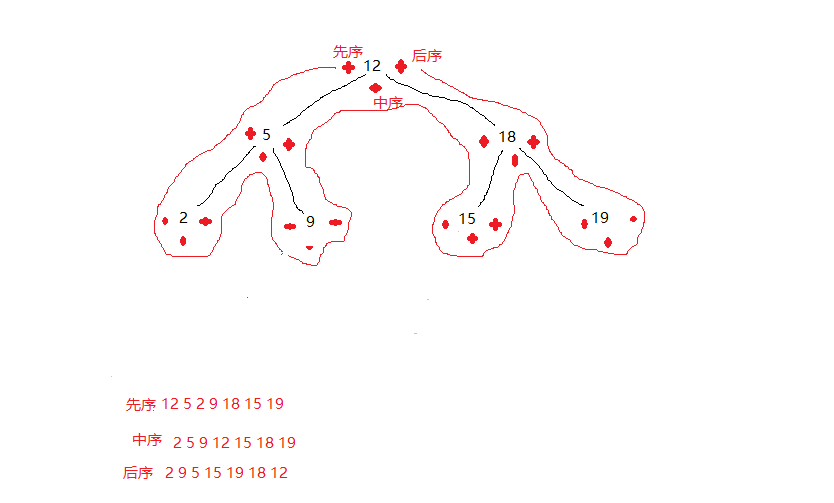
三种遍历的本质:访问路径一样,访问顺序不一样。
先序遍历:根左右,先访问根节点、再左节点、其次右节点
中序遍历:左根右,先访问左节点、再根节点、其次右节点
后序遍历:左右根,先访问左节点、再右节点、其次根节点
用上面的图解释这句话,那条红线就是访问路径,三种遍历方式都是这条访问路径;用节点旁边的三个红点来表示访问和顺序,这么说,可能还是懵。
拿先序来举个例子吧:访问路径一样,都从根节点12出发,遇到“先序红点”,直接输出12,然后是5,最后的先序结果上图下面的结果。
(1)先序遍历
先序遍历程序如下:
// 对以node为根的二叉搜索树进行先序遍历 void preOrder(Node* node) { if (node != NULL) { cout << node->key << endl; preOrder(node->left); preOrder(node->right); } }
(2)中序遍历
中序遍历程序如下:
// 对以node为根的二叉搜索树进行中序遍历 void inOrder(Node* node) { if (node != NULL) { inOrder(node->left); cout << node->key << endl; inOrder(node->right); } }
(3)后序遍历
后序遍历程序如下:
// 对以node为根的二叉搜索树进行后序遍历 void postOrder(Node* node) { if (node != NULL) { postOrder(node->left); postOrder(node->right); cout << node->key << endl; } }
6、总体程序
总体的程序如下,方便调试和使用,程序如下:

#include <iostream> #include <queue> #include <cassert> #include<ctime> using namespace std; template <typename Key, typename Value> class BST { private: struct Node { Key key; Value value; Node *left; Node *right; Node(Key key, Value value) { this->key = key; this->value = value; this->left = this->right = NULL; } Node(Node *node) { this->key = node->key; this->value = node->value; this->left = node->left; this->right = node->right; } }; Node *root; int count; public: BST() { root = NULL; count = 0; } ~BST() { destroy(root); } int size() { return count; } bool isEmpty() { return count == 0; } void insert(Key key, Value value) { root = insert(root, key, value); } bool contain(Key key) { return contain(root, key); } Value* search(Key key) { return search(root, key); } // 前序遍历 void preOrder() { preOrder(root); } // 中序遍历 void inOrder() { inOrder(root); } // 后序遍历 void postOrder() { postOrder(root); } // 层序遍历 void levelOrder() { queue<Node*> q; q.push(root); while (!q.empty()) { Node *node = q.front(); q.pop(); cout << node->key << endl; if (node->left) q.push(node->left); if (node->right) q.push(node->right); } } // 寻找最小的键值 Key minimum() { assert(count != 0); Node* minNode = minimum(root); return minNode->key; } // 寻找最大的键值 Key maximum() { assert(count != 0); Node* maxNode = maximum(root); return maxNode->key; } // 从二叉树中删除最小值所在节点 void removeMin() { if (root) root = removeMin(root); } // 从二叉树中删除最大值所在节点 void removeMax() { if (root) root = removeMax(root); } // 从二叉树中删除键值为key的节点 void remove(Key key) { root = remove(root, key); } private: // 向以node为根的二叉搜索树中,插入节点(key, value) // 返回插入新节点后的二叉搜索树的根 Node* insert(Node *node, Key key, Value value) { if (node == NULL) { count++; return new Node(key, value); } if (key == node->key) node->value = value; else if (key < node->key) node->left = insert(node->left, key, value); else // key > node->key node->right = insert(node->right, key, value); return node; } // 查看以node为根的二叉搜索树中是否包含键值为key的节点 bool contain(Node* node, Key key) { if (node == NULL) return false; if (key == node->key) return true; else if (key < node->key) return contain(node->left, key); else // key > node->key return contain(node->right, key); } // 在以node为根的二叉搜索树中查找key所对应的value Value* search(Node* node, Key key) { if (node == NULL) return NULL; if (key == node->key) return &(node->value); else if (key < node->key) return search(node->left, key); else // key > node->key return search(node->right, key); } // 对以node为根的二叉搜索树进行前序遍历 void preOrder(Node* node) { if (node != NULL) { cout << node->key << endl; preOrder(node->left); preOrder(node->right); } } // 对以node为根的二叉搜索树进行中序遍历 void inOrder(Node* node) { if (node != NULL) { inOrder(node->left); cout << node->key << endl; inOrder(node->right); } } // 对以node为根的二叉搜索树进行后序遍历 void postOrder(Node* node) { if (node != NULL) { postOrder(node->left); postOrder(node->right); cout << node->key << endl; } } void destroy(Node* node) { if (node != NULL) { destroy(node->left); destroy(node->right); delete node; count--; } } // 在以node为根的二叉搜索树中,返回最小键值的节点 Node* minimum(Node* node) { if (node->left == NULL) return node; return minimum(node->left); } // 在以node为根的二叉搜索树中,返回最大键值的节点 Node* maximum(Node* node) { if (node->right == NULL) return node; return maximum(node->right); } // 删除掉以node为根的二分搜索树中的最小节点 // 返回删除节点后新的二分搜索树的根 Node* removeMin(Node* node) { if (node->left == NULL) { Node* rightNode = node->right; delete node; count--; return rightNode; } node->left = removeMin(node->left); return node; } // 删除掉以node为根的二分搜索树中的最大节点 // 返回删除节点后新的二分搜索树的根 Node* removeMax(Node* node) { if (node->right == NULL) { Node* leftNode = node->left; delete node; count--; return leftNode; } node->right = removeMax(node->right); return node; } // 删除掉以node为根的二分搜索树中键值为key的节点 // 返回删除节点后新的二分搜索树的根 Node* remove(Node* node, Key key) { if (node == NULL) return NULL; if (key < node->key) { node->left = remove(node->left, key); return node; } else if (key > node->key) { node->right = remove(node->right, key); return node; } else { // key == node->key if (node->left == NULL) { Node *rightNode = node->right; delete node; count--; return rightNode; } if (node->right == NULL) { Node *leftNode = node->left; delete node; count--; return leftNode; } // node->left != NULL && node->right != NULL Node *successor = new Node(minimum(node->right)); count++; successor->right = removeMin(node->right); successor->left = node->left; delete node; count--; return successor; } } }; void shuffle(int arr[], int n) { srand(time(NULL)); for (int i = n - 1; i >= 0; i--) { int x = rand() % (i + 1); swap(arr[i], arr[x]); } } int main() { srand(time(NULL)); BST<int, int> bst = BST<int, int>(); int n = 10; for (int i = 0; i < n; i++) { int key = rand() % n; // 为了后续测试方便,这里value值取和key值一样 int value = key; //cout<<key<<" "; bst.insert(key, value); } // test remove // remove elements in random order int order[10] = {0}; for (int i = 0; i < n; i++) order[i] = i; shuffle(order, n); for (int i = 0; i < n; i++) if (bst.contain(order[i])) { bst.remove(order[i]); cout << "After remove " << order[i] << " size = " << bst.size() << endl; } system("pause"); return 0; }
总结:
坚持学习与分享!喜欢的帮忙推荐,有问题欢迎随时留言!
