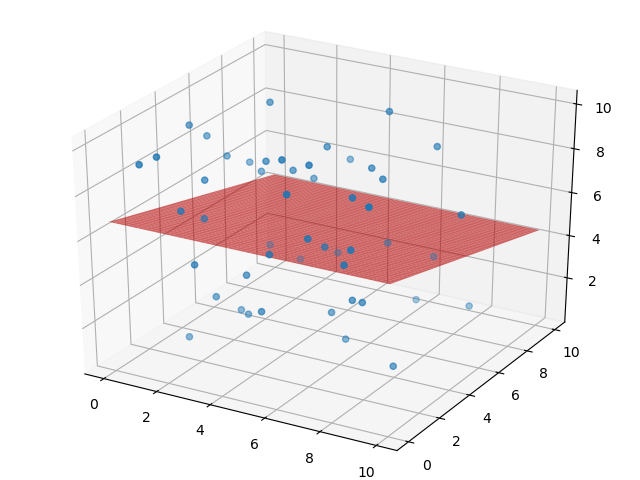
对于2个变量的样本回归分析,L2和L1正则化基本相同,仅仅正则化项不同
LASSO回归为在损失函数加入(||omega||_1) ,(omega) 的1范数 而 岭回归为(||omega||_2^2),(omega) 的2范数
*矩阵、向量范数
*L1正则化(岭回归)
LASSO Regression
Loss Function
[J(omega)= (X omega - Y)^T(X omega - Y) + lambda ||omega||_1
]
(||omega||_1)导数不连续,采用坐标下降法求(omega)
坐标下降法推导过程
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
M = 3 #变量个数+1 变量加 偏移项b, 一个3个参数
N = 50 #样本个数
#随机生成两个属性的N个样本
feature1 = np.random.rand(N)*10
feature2 = np.random.rand(N)*10
splt = np.ones((1, N))
#
temp_X1 = np.row_stack((feature1, feature2))
temp_X = np.vstack((temp_X1, splt))
X_t = np.mat(temp_X)
X = X_t.T
temp_Y = np.random.rand(N)*10
Y_t = np.mat(temp_Y)
Y = Y_t.T
#画样本散点图
fig = plt.figure()
ax1 = Axes3D(fig)
ax1.scatter(feature1, feature2, temp_Y)
######
def errors(X, Y, Omega) :
err = (X*Omega - Y).T*(X*Omega - Y)
return err
#坐标下降算法
def lasso_regression(X, Y, lambd, threshold):
#
Omega = np.mat(np.zeros((M, 1)))
err = errors(X, Y, Omega)
counts = 0 #统计迭代次数
# 使用坐标下降法优化回归系数Omega
while err > threshold:
counts += 1
for k in range(M):
# 计算常量值z_k和p_k
z_k = (X[:, k].T*X[:, k])[0, 0]
p_k = 0
for i in range(N):
p_k += X[i, k]*(Y[i, 0] - sum([X[i, j]*Omega[j, 0] for j in range(M) if j != k]))
if p_k < -lambd/2:
w_k = (p_k + lambd/2)/z_k
elif p_k > lambd/2:
w_k = (p_k - lambd/2)/z_k
else:
w_k = 0
Omega[k, 0] = w_k
err_prime = errors(X, Y, Omega)
delta = abs(err_prime - err)[0, 0]
err = err_prime
print('Iteration: {}, delta = {}'.format(counts, delta))
if delta < threshold:
break
return Omega
#求Omega
lambd = 10.0
threshold = 0.1
Omega = lasso_regression(X, Y, lambd, threshold)
#画分回归平面
xx = np.linspace(0,10, num=50)
yy = np.linspace(0,10, num=50)
xx_1, yy_1 = np.meshgrid(xx, yy)
Omega_h = np.array(Omega.T)
zz_1 = Omega_h[0, 0]*xx_1 + Omega_h[0, 1]*yy_1 + Omega_h[0, 2]
ax1.plot_surface(xx_1, yy_1, zz_1, alpha= 0.6, color= "r")
plt.show()
效果