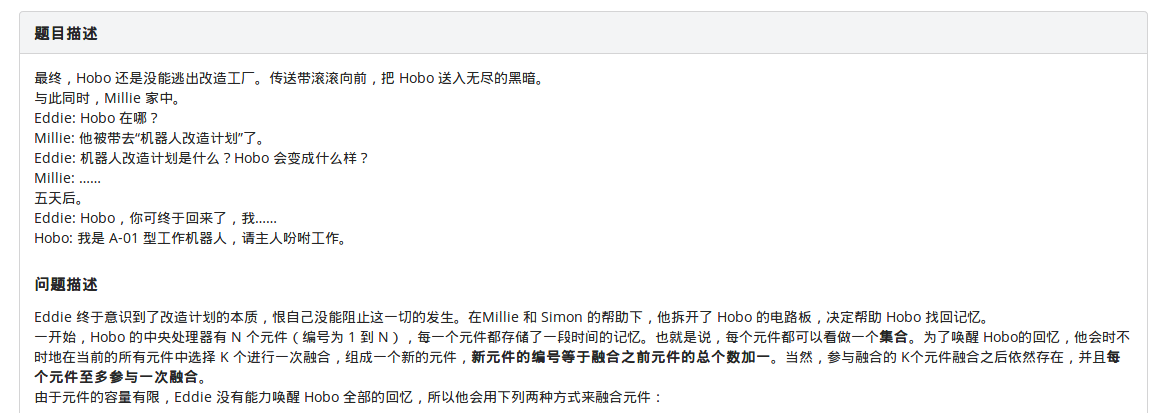
题目描述

分析
考虑离线处理之后建树
如果 (a_1,a_2,...,a_k) 的交是 (b)
那我们从 (b) 到 (a_1,a_2,...,a_k) 建一条边权为 (0) 的边
同样地,如果 (a_1,a_2,...,a_k) 的并是 (b)
那我们从 (b) 到 (a_1,a_2,...,a_k) 建一条边权为 (1) 的边
(k=1) 既是交又是并,要特殊处理一下,可以建边权为 (2) 的边
询问时,我们通过 (dfn) 序判断两个节点是否有父子关系
如果没有,直接输出 (0)
否则如果 (x) 是 (y) 的祖先,当(x) 到 (y) 的路径中边权只为 (0) 或 (2) 时输出 (1)
如果 (y) 是 (x) 的祖先,当(x) 到 (y) 的路径中边权只为 (1) 或 (2) 时输出 (1)
其它情况输出 (0)
代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
int n,m,now,h[maxn],tot=1;
struct asd{
int to,nxt,val;
}b[maxn<<1];
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
int dfn[maxn],siz[maxn],dfnc,dep[maxn],dis[maxn],du[maxn],haha[maxn];
void dfs(int now,int fa){
dfn[now]=++dfnc;
siz[now]=1;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(u==fa) continue;
haha[u]=haha[now];
if(b[i].val==2) haha[u]++;
dep[u]=dep[now]+b[i].val;
dis[u]=dis[now]+1;
dfs(u,now);
siz[now]+=siz[u];
}
}
int pd(int aa,int bb){
if(dfn[aa]>dfn[bb] && dfn[aa]<=dfn[bb]+siz[bb]-1) return bb;
if(dfn[bb]>dfn[aa] && dfn[bb]<=dfn[aa]+siz[aa]-1) return aa;
return 0;
}
int x[maxn],y[maxn],cnt;
int main(){
memset(h,-1,sizeof(h));
n=read(),m=read();
now=n;
rg int aa,bb,cc,dd;
for(rg int i=1;i<=m;i++){
aa=read(),bb=read(),cc=read();
if(aa==0){
now++;
if(cc==1){
dd=read();
ad(dd,now,2);
ad(now,dd,2);
du[dd]++;
} else if(bb==0){
for(rg int j=1;j<=cc;j++){
dd=read();
ad(now,dd,0);
du[dd]++;
}
} else {
for(rg int j=1;j<=cc;j++){
dd=read();
ad(now,dd,1);
du[dd]++;
}
}
} else {
x[++cnt]=bb;
y[cnt]=cc;
}
}
for(rg int i=1;i<=now;i++){
if(du[i]==0){
dfs(i,0);
}
}
for(rg int i=1;i<=cnt;i++){
rg int now=pd(x[i],y[i]);
if(x[i]==y[i]) printf("1
");
else if(now==0) printf("0
");
else if(now==x[i]){
if(dep[x[i]]-dep[y[i]]==(haha[x[i]]-haha[y[i]])*2) printf("1
");
else printf("0
");
} else {
if(dep[y[i]]-dep[x[i]]==dis[y[i]]-dis[x[i]]+haha[y[i]]-haha[x[i]]) printf("1
");
else printf("0
");
}
}
return 0;
}