写在前面:这道题并不是简单的思维题,而是一道数学题,所以大家一定要认真推理,不要直接抄代码,理解最重要
题目描述

输入格式
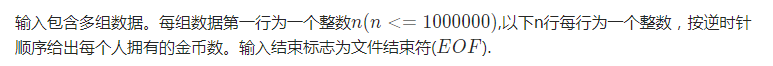
输出格式

输入输出样例
输入样例

3 100 100 100 4 1 2 5 4
输出样例

0 4
一句话题意:有n个人围成一圈,每个人有一定数量的金币,每个人可以给和他相邻的人一些金币,求挪动的最少金币使他们平分金币
分析
对于每一个人,他的金币数只能从他前面那一个人或者后面那一个人那里得到
同样地,他的金币也只能传递给前面的那个人或者后面的那个人
但是无论怎么传递,他们最终剩余的金币数是相同的,而且这个金币数我们可以直接算出来
我们设最终每个人都有的金币数为m,人数为n
在读入时,我们开一个变量ans记录n个人的金币数之和,那么m=ans/n
我们设b[i]为第i个人给第i-1个人的金币数,需要注意的是,因为题目中说n个人围成了一个环,所以b[1]为第1个人给第n个人的金币数
(注意,这里的b数组可正可负,如果是正数,表明第i个人给了第i-1个人金币,如果为负数,表明第i-1个人给了第i个人金币,如果为0,则两个人不发生金币交换)
对于第一个人,他给了第n个人b[1]个金币,同时,第二个人又给了他b[2]个金币,他的初始金币数为a[1],最终金币数为m
所以我们可以列出式子 m=a[1]-b[1]+b[2] -------- 1式
同样,对于第二个人 m=a[2]-b[2]+b[3] -------- 2式
……
对于第n个人:m=a[n]-b[n]+b[1] -------- n式
所以m=a[n]-b[n]+b[n+1]
为了找规律方便,我们引入一个数组c,令c[1]=a[1]-m,c[2]=a[1]+a[2]-m*2,c[n]=a[1]+a[2]+...+a[n]-m*n
通式为c[0]=0,c[i]=a[i]+c[i-1]-m;
对于第二个人(由1式得):b[2]=m-a[1]+b[1]=b[1]-c[1];
对于第三个人(由2式得):b[3]=m-a[2]+b[2]=m-a[2]+m-a[1]+b[1](将b[2]=m-a[1]+b[1]代入)=2m-a[1]-a[2]+b[1]=b[1]-c[2];
对于第四个人(由3式得):b[4]=m-a[3]+b[3]=3m-a[1]-a[2]-a[3]+b[1]=b[1]-c[3]
……
我们希望所有的b[i]的绝对值之和尽量小,也就是使
|b[1]-c[0]|+|b[1]-c[1]|+|b[1]-c[2]|+|b[1]-c[3]|+……+|b[1]-c[n-1]|最小
对于任意两个数a、b,我们知道|a-b|的绝对值表示它们在数轴上的距离
所以原式我们可以看成坐标为b[1]的点到以上所有点距离之和的最小值
这时,就有一个结论,给定数轴上的n个点,在数轴上所有点中,中位数离所有顶点的距离之和最小
下面我们给出简单的证明
如果n为奇数,我们举一个5的例子
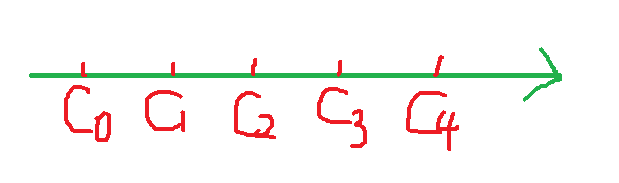
根据结论,这时c2点为最优决策
我们用反证法,如果我们将决策点向左移动一个单位,那么该点到c0、c1的距离分别减小1,到c2、c3、c4的距离分别增加1,总的距离增加了1,显然不是最优决策
如果我们将决策点向右移动一个单位,那么该点到c0、c1、c2的距离分别增加1,到c3、c4的距离分别减小1,总的距离增加了1,显然不是最优决策
所以中位数最优
同样的,如果n为偶数,我们只需要在[c[n/2-1],c[n/2]]这个区间内任取一个数就是最优决策,证明同上
不要忘了排一下序
所以,最终我们要将b[1]的值赋值成c[n/2]
而c数组我们提前处理得到,所以问题就迎刃而解了
到这里,其实b数组并没有什么用,只是在证明过程中出现,所以我们只要定义一个整形变量存储b[1]就可以了
记得要开long long哦
代码

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 const int maxn=1e6+5; 8 typedef long long ll;//注意要开long long 9 ll a[maxn],c[maxn]; 10 ll n; 11 int main(){ 12 while(scanf("%d",&n)!=EOF){ 13 memset(c,0,sizeof(c)); 14 memset(a,0,sizeof(a)); 15 ll tot=0; 16 for(ll i=1;i<=n;i++){ 17 scanf("%lld",&a[i]); 18 tot+=a[i]; 19 } 20 ll pj=tot/n;//求出每个人最终拥有的金币数 21 for(ll i=1;i<n;i++){ 22 c[i]=a[i]+c[i-1]-pj; 23 }//预处理c数组 24 sort(c,c+n);//排序,不要忘了 25 ll ans=c[n/2]; 26 ll cnt=0; 27 for(ll i=0;i<n;i++){ 28 cnt+=abs(ans-c[i]); 29 } 30 printf("%lld ",cnt); 31 } 32 return 0; 33 }
