看了很多大佬的博客,每看一篇博客懂一部分,总算是大概理解了树状数组这个神奇又强大的东西;
在这里我做个整合,把我认为好的部分摘录下来;
参考博客1:https://blog.csdn.net/flushhip/article/details/79165701
参考博客2:https://blog.csdn.net/int64ago/article/details/7429868
下面是这两位大佬写的乐章合奏篇~~~~~~~~
首先,我们需要通篇以二进制的视角来学习树状数组,树状数组就是应用二进制的特点来简化不必要的计算过程,利用位运算以实现高效的增删改查;
说到树状数组,顾名思义,这两幅图完全体现了它的核心思想;
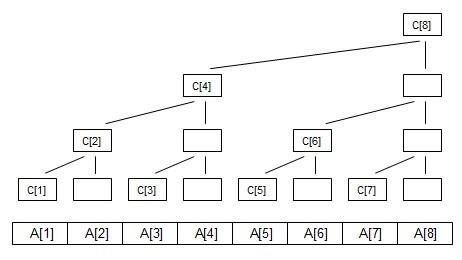
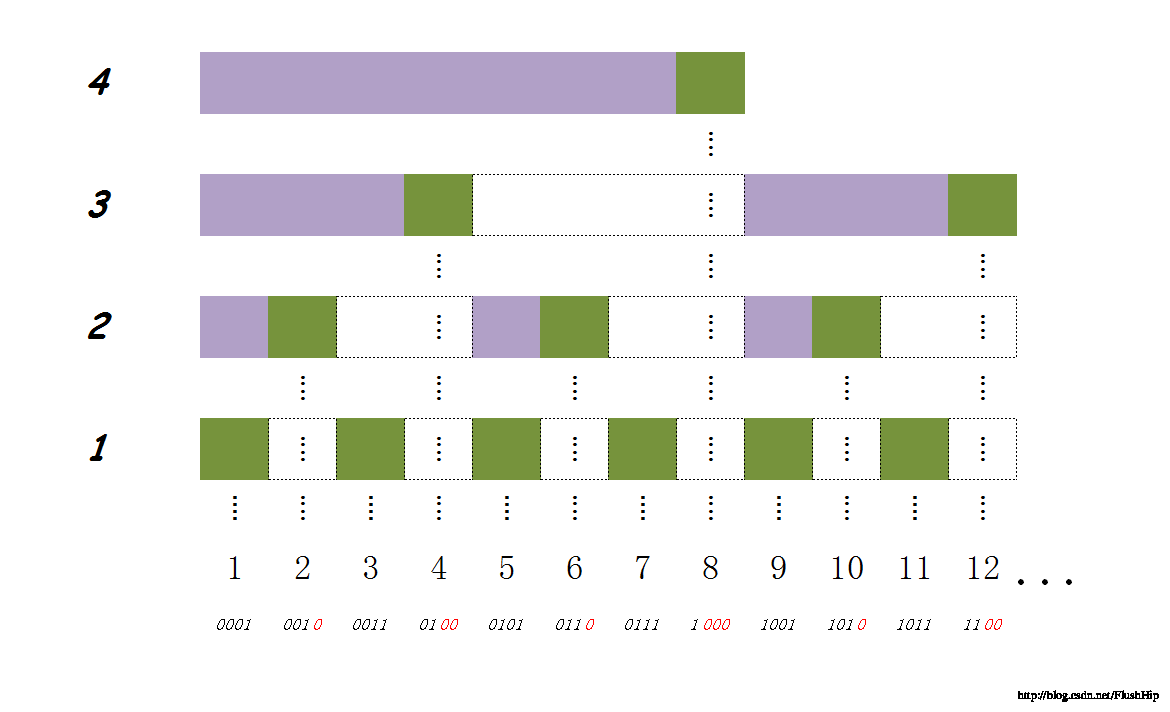
树状数组的作用
首先我们搞明白树状数组是用来干嘛的,现在有一个这样的问题:有一个数组a,下标从0到n-1,现在给你w次修改,q次查询,修改的话是修改数组中某一个元素的值;查询的话是查询数组中任意一个区间的和;
这个问题很常见,首先分析下朴素做法的时间复杂度,修改是O(1)O(1)的时间复杂度,而查询的话是O(n)O(n)的复杂度,总体时间复杂度为O(qn)O(qn);可能你会想到前缀和来优化这个查询,我们也来分析下,查询的话是O(1)O(1)的复杂度,而修改的时候修改一个点,那么在之后的所有前缀和都要更新,所以修改的时间复杂度是O(n)O(n),总体时间复杂度还是O(qn)O(qn)。
可以发现,两种做法中,要么查询是O(1)O(1),修改是O(n)O(n);要么修改是O(1)O(1),查询是O(n)O(n)。那么就有没有一种做法可以综合一下这两种朴素做法,然后整体时间复杂度可以降一个数量级呢?有的,对,就是树状数组。
树状数组的思想
假设数组a是我们增删改查的对象,但树状数组的思想维护的是 c 数组, 从上面的图我们可以看到,c[i]不是通常意义上的1~i 元素的和;
由图来看看c数组的规则,其中c8 = c4+c6+c7+a8,c6 = c5+a6……先不必纠结怎么做到的,我们只要知道c数组的大致规则即可,很容易知道c8表示a1~a8的和,但是c6却是表示a5~a6的和,为什么会产生这样的区别的呢?或者说发明她的人为什么这样区别对待呢?答案是,这样会使操作更简单!看到这相信有些人就有些感觉了,为什么复杂度被lg了呢?可以看到,c8可以看作a1~a8的左半边和+右半边和,而其中左半边和是确定的c4,右半边其实也是同样的规则把a5~a8一分为二……继续下去都是一分为二直到不能分,可以看看B图。说白了树状数组就是巧妙的利用了二分!
具体如何一分为二的规则通过 lowbit() 函数实现;
lowbit函数
lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1,举个例子,x = 6,它的二进制为110,那么lowbit(x)就返回2。
那么怎么求lowbit呢?
-
先消掉最后一位
1,然后再用原数减去消掉最后一位1后的数,答案就是lowbit(x)的结果; -
第二种方法就是计算机组成原理课上老师教过我们求负数的补码的简便方法:把这个数的二进制写出来,然后从右向左找到第一个
1(这个1就是我们要求的结果,但是现在表示不出来,后来的操作就是让这个1能表示出来),这个1不要动和这个1右边的二进制不变,左边的二进制依次取反,这样就求出的一个数的补码,说这个方法主要是让我们理解一个负数的补码在二进制上的特征,然后我们把这个负数对应的正数与该负数与运算一下,由于这个1的左边的二进制与正数的原码对应的部分是相反的,所以相与一定都为0,;由于这个1和这个1右边的二进制都是不变的,因此,相与后还是原来的样子,故,这样搞出来的结果就是lowbit(x)的结果。
两种方法对应的代码依次如下:
1 int lowbit(x) 2 { 3 return x - (x & (x - 1)); 4 }
int lowbit(x) { return x & -x; }
树状数组的实现
更新操作:只要更新修改这个点会影响到的c数组,假设现在修改6(110)这个点,依据树状数组的性质三,它影响的直系父层就是c[6(110) + lowbit(6(110))] = c[8(1000)],但是它肯定不是只影响直系父层,上面所有包含这一层和的层都要更新,但是我们把这个更新传递给直系父层c[8],8这个点的直系父层是c[16],依次类推地更新就行了;
查询前缀和:
1 int sum(int x, ArrayInt c, int n) 2 { 3 int ret = 0; 4 for ( ; x > 0; ret += c[x], x -= lowbit(x)); 5 return ret; 6 }
更新操作:
1 void update(int x, int val, ArrayInt c, int n) 2 { 3 for ( ; x <= n; c[x] += val, x += lowbit(x)); 4 }