这里主要针对上篇的sort排序算法进行简单的总结,具体代码实现和分析见
排序sort(一):http://www.cnblogs.com/liuamin/p/6698307.html
先贴一张图:(网上找的)
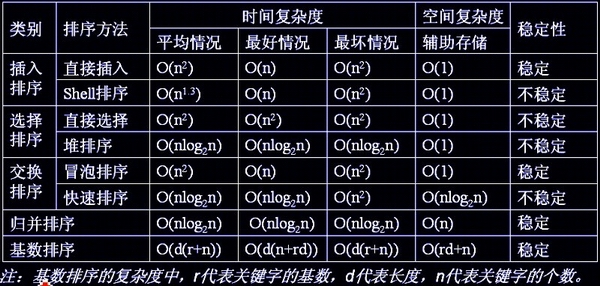
上图分别是各个算法的时间复杂度和稳定性分析。下面我的总结顺序和其中的部分片段代码和上篇http://www.cnblogs.com/liuamin/p/6698307.html一样。
(1)交换排序
交换排序包括:冒泡排序和快速排序。
【1】首先冒泡排序是相邻的元素之间进行比较,当无序时进行交换,相等时不交换(所以是稳定的排序算法),直到有序。
时间复杂度分析:
最好的情况下是序列本身有序,则只要进行
for (int j = a.size() - 2; j >= i; j--)
这里的一轮比较,也就是n-1次比较,标志位为false,则说明元素有序,没有交换,所以时间复杂度为o(n)。
最坏情况下是元素逆序,这里需要进行
for (int i = 0; i<a.size() && change; i++) for (int j = a.size() - 2; j >= i; j--)
i等于每一个值都要进行一轮比较,直到 i<a.size(),也就是进行了(n-1)+........3+2+1=n(n-1)/2次比较,同时移动(交换)了等量的次数。所以时间复杂度为0(n^2)。
平均情况也是0(n^2)。
空间复杂度分析:
这里当元素无序时,要进行交换元素(swap函数),借助了一个辅助空间,所以空间复杂度为0(1)。
【2】快速排序主要是对序列的【low到high】选择pivotkey,使得它左边元素均小于它,右边的元素均大于它,返回pivotkey的下标pivot,然后再对这两部分
(【low到pivot-1】和【pivot+1到high】)重复进行快排,(递归)这里比较和交换是跳跃的,所以是不稳定的排序方法。
时间复杂度分析:
快排最坏情况下,pivotkey选择的不好,刚好是里面最大(最小)的元素,递归树是一个斜树(递归深度为n-1),也就是进行n-1次调用,第i次调用需要比较n-i次才能找到pivot, i从1到n-1,也就是比较(n-1)+........3+2+1=n(n-1)/2次,(当i=1时,比较n-1,i等于2时,比较n-2,.......,i等于n-1时,比较1次),所以时间复杂度为o(n^2)。
最好情况下,pivotkey选择的较好,是中间元素,所以每次划分的很均匀,递归树的深度为log(2n)+1,通过不等式推断,时间复杂度为o(nlog2n)。
平均情况下,数学归纳法证明,数量级为o(nlog2n)。
空间复杂度分析:
空间复杂度,主要是递归造成的栈空间,最坏是递归深度为n-1,空间复杂度为o(n),好的情况下为o(log2n),所以平均情况空间复杂度为o(log2n)。
(2)选择排序
选择排序包括简单选择排序和堆排序
【1】简单选择排序是每一轮比较后选择好最小(最大)的元素之后再进行交换,优点在于不进行频繁的交换,它是选择最小的元素进行交换,是跳跃式交换,所以是不稳定的排序算法。
for (int i = 0; i < a.size(); i++) for (int j = i + 1; j < a.size(); j++)
时间复杂度分析:
最好,最坏情况下都是比较(n-1)+........3+2+1=n(n-1)/2次,但最好情况下不交换(0次),最坏情况下也只交换n-1次。
因此简单选择排序最好,最坏,平均复杂度均为o(n^2)。
空间复杂度分析:
空间复杂度和冒泡排序类似,swap函数,借助辅助空间,所以空间复杂度为o(1)。
【2】堆排序是建立好大顶堆(小顶堆),交换(移走)最大(最小)的堆顶元素,再对剩下的n-1个元素重建堆,如此重复。。。
这里交换是跳跃的,也就是交换的是堆顶元素和堆底元素,所以是不稳定的排序方法。
swap(a[0], a[i]);
时间复杂度分析:
它所用时间主要消耗在开始建堆,和后面重建堆的时间上,开始建堆是针对非叶节点进行(约等于堆元素的一半),时间复杂度为o(n),推导见算法导论。
for (int i = (a.size() - 2) / 2; i >= 0; i--) HeapAdjust(a, i, a.size());
对重建堆,每次对剩下的i-1个元素进行重建,重建的复杂度为o(log2n),(完全二叉树的深度,n为剩下的节点数目,n=i-1,),需要取n-1次,所以时间复杂度为o(nlog2n)。
for (int i = a.size() - 1; i>0;i--) { swap(a[0], a[i]); HeapAdjust(a, 0,i-1); }
通过分析堆排序对原始记录的排序并不敏感,所以最好,最坏,平均时间复杂度都为o(nlog2n)。
空间复杂度分析:
空间复杂度也是swap函数(一个交换的暂存单元),所以空间复杂度为o(1)。
注:它的时间复杂度主要在堆的建立上,所以不适合排序元素少的序列。。
(3)插入排序
插入排序包括直接插入排序和希尔排序
【1】直接插入排序是将一个记录插入到已经排序好的有序表中,从而得到一个新的,记录数增1的有序表。i从1开始,每次将a[i]和a[i-1]进行比较,如果无序,则将元素后移,直到找出正确的位置插入a[i]。当插入的第i个元素如果与之前一个元素相等,插入的位置为相等元素a[i-1]的后面,所以是一种稳定的排序算法。
时间复杂度分析:
最坏的情况是i每为一个数,for循环要比较i-1次,i从1到n-1,所以比较了1+2+3......+(n-1)=n(n-1)/2次,交换次数也是n^2数量级的,所以时间复杂度为o(n^2),但是和冒泡和简单选择排序相比,直接插入排序性能好一点。
if (a[i] < a[i - 1]) for (j = i - 1; j >= 0 && temp < a[j]; j--)
最好的情况是比较了n-1次(a[i]和a[i-1]比较),不需要交换(0次)。
平均情况时间复杂度也是o(n^2)。
空间复杂度分析:
这里借助了一个temp的交换暂存空间,所以空间复杂度为o(1)。
【2】希尔排序是跳跃式的向前移动(a[i] 与a[i - increasment]比较),跳跃的距离取决于增量序列 increasment,但最后的增量值一定是1,这样和直接插入排列一样,但移动的次数大大减小,因为元素已经基本有序。因为是跳跃式的移动和比较,所以是一种不稳定的排序方法。
时间复杂度分析:
希尔排序时间复杂度分析很难,它比较次数与移动(交换)次数依赖于增量因子序列increasment的选取,目前还没有人给出选取最好的增量因子序列的方法。增量因子序列可以有各种取法,但是最后一个增量因子必须为1。大量的研究表明当取得合适的增量因子序列时,时间复杂度为o(n^3/2),效率高于n^2。
空间复杂度分析:
与直接插入排序一样,也是借助了一个temp的交换暂存空间,所以空间复杂度为o(1)。
(4)归并排序是借助辅助空间temp[ ],将待排序序列a分成若干个子序列,再进行归并为有序的temp[ ],之后再把有序的temp[ ]归并为整体有序序列a,因为它比较元素时如果相等,先将位于序列前面的元素归并在前面,所以不会改变相等元素的顺序,是一种稳定的排序方法。
空间复杂度分析:
归并排序有两种实现方式:第一种是递归方法实现,空间复杂度除了temp[ ],还有递归用到的栈空间,所以整体的空间复杂度为o(n+log2n);
另一种是非递归方法,只有辅助空间temp[ ],所以它的空间复杂度为o(n),
因此归并排序更推荐使用非递归归并排序方法。
时间复杂度分析:
所有元素扫描时间为n(MergePass函数),再进行归并排序要进行 o(log2n)次(由完全二叉树的深度确定,while循环),所以时间复杂度为o(nlog2n)。
注:归并排序是一种比较占内存的排序方式,(利用空间换取了时间),但很高效稳定。
综上:
像冒泡,简单选择排序和直接插入排序,适合待排序序列的元素个数不是很多的情况,他们的平均时间复杂度和空间复杂度都是一样的,且都是稳定的。
当待排序序列的元素个数不是很多时,选择直接插入排序,但是如果每个元素的关键字记录很大(占内存)时,则选择简单选择排序,因为它移动次数少,最多才n-1次。
当序列元素个数很多时,选择快速排序,但是要求稳定时,选择归并排序,但是归并排序又比较占内存。。
所以要根据自己需求和具体分析,选择合适的排序方法。。