dinic 网络流算法 :
网络流数组要开大一点
反悔边的意义:当一条流量被流入,反向流入的时候,就相当于没有流过。
分层图的意义:对于给定的点,流入< =dep[ u ] 是没有意义的,不会使得当前流更优。
当前弧优化:当前的边已经流光,不再流入。
炸点优化:当前点已经流光,设dep为-1,不再流入。
多路增广:如果一个点可以多条流出去,一次dfs多条路径。
BFS :每次建立一个分层图。
DFS:流过一条流
最大流=最小割
P3376 【模板】网络最大流
模板。
 View Code
View Code1001: [BeiJing2006]狼抓兔子
一个1e6的图,求最小割,数组开小了,TLE
 View Code
View Code网络流24题:
P2756 飞行员配对方案问题
简单二分图匹配,

#include<bits/stdc++.h> using namespace std; #define pb push_back const int N=1e3+5; int gp[N][N],match[N],vis[N]; int n,m; bool findpath(int u){ for(int i=m+1;i<=n+m;i++){ if(gp[u][i]&&!vis[i]){ vis[i]=1; if(!match[i]||findpath(match[i])){ match[i]=u; return 1; } } } return 0; } void init(){ memset(gp,0,sizeof gp); memset(match,0,sizeof match); } int main(){ init(); scanf("%d %d",&m,&n); int u,v; while(~scanf("%d %d",&u,&v)){ if(u+v<0)break; gp[u][v]=1; } vector<int>ans; for(int i=1;i<=m;i++){ memset(vis,0,sizeof vis); if(findpath(i))ans.pb(i); } for(int i=m+1;i<=n+m;i++){ if(match[i])match[ match[i] ]=i; } cout<<ans.size()<<endl; for(int i=0;i<ans.size();i++){ printf("%d %d ",ans[i],match[ ans[i] ]); } // system("pause"); return 0; }
P4015 运输问题
将源点到每个仓库连一条费用为0,流量为 a [ i ] 的边,仓库与店铺连一条边,最后所有店铺与汇点连一条费用为0,流量为b [ i ] 的边;
跑一遍费用流即可。然后最大费用就是把费用全部变负,跑一遍费用流,然后最后结果取负即可。
但数组开小了,汇点越界,

#include<bits/stdc++.h> using namespace std; const int N=1e4+50; const int inf=0x3f3f3f3f; int a[200],b[200],c[200][200]; int n,m,S,T; int mincost; struct Dinic{ int head[N],dis[N],pre[N],flow[N],last[N]; bool inq[N]; int ecnt; struct edge{ int v,w,flow,next; }e[N*10]; void init(){ memset(head,-1,sizeof head); ecnt = 0; } void addedge(int u,int v,int w,int flow){ e[ecnt].v=v;e[ecnt].w=w;e[ecnt].flow=flow;e[ecnt].next=head[u];head[u]=ecnt++; } bool spfa(){ memset(dis,inf,sizeof dis); memset(flow,inf,sizeof flow); memset(inq,0,sizeof inq); queue<int>Q; Q.push(S);inq[S]=1;dis[S]=0;pre[T]=-1; while(!Q.empty()){ int u=Q.front();Q.pop();inq[u]=0; for(int i=head[u];~i;i=e[i].next){ int v=e[i].v,w=e[i].w; if(e[i].flow>0&&dis[v]>dis[u]+w){ dis[v]=dis[u]+w;pre[v]=u;last[v]=i; flow[v]=min(flow[u],e[i].flow); if(!inq[v]){ Q.push(v);inq[v]=1; } } } } return pre[T]!=-1; } void MCMF(){ mincost=0; while(spfa()){ int cur=T; mincost+=flow[T]*dis[T]; while(cur!=S){ e[last[cur]].flow-=flow[T]; e[last[cur]^1].flow+=flow[T]; cur=pre[cur]; } } } }dinic; void init_add(int t){ for(int i=1;i<=m;i++){ dinic.addedge(S,i,0,a[i]); dinic.addedge(i,S,0,0); } for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ dinic.addedge(i,j+m,t*c[i][j],b[j]); dinic.addedge(j+m,i,-c[i][j]*t,0); } } for(int i=1;i<=n;i++){ dinic.addedge(i+m,T,0,b[i]); dinic.addedge(T,i+m,0,0); } } int main(){ scanf("%d %d",&m,&n); S=0,T=10005; for(int i=1;i<=m;i++)scanf("%d",&a[i]); for(int i=1;i<=n;i++)scanf("%d",&b[i]); for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ scanf("%d",&c[i][j]); } } dinic.init(); init_add(1); dinic.MCMF(); printf("%d ",mincost); dinic.init(); init_add(-1); dinic.MCMF(); printf("%d ",-mincost); // system("pause"); return 0; }
C - C
题意:一张图,找出p条路径,每条路径的流均为x,求最大的p*x;
考虑直接流就是每一条流增广流量为x,但这样不好check;
于是考虑如下做法,把每一条流 拆成 f / x , 最后判断最大流流是否大于p即可。
二分精度注意,小了大了都会爆。

#include<bits/stdc++.h> using namespace std; typedef double db; const db eps=1e-6; const int inf=0x3f3f3f3f; const int N=1e4+5; int n,m,S,T; struct Dinic{ int head[N],dep[N]; int ecnt; struct edge{ int v,flow,next; }e[N*10]; void init(){ memset(head, -1, sizeof head); ecnt = 0; } void addedge(int u, int v, int flow) { e[ecnt].v=v;e[ecnt].flow=flow;e[ecnt].next=head[u];head[u]=ecnt++; } bool BFS(){//分层图找增广路 memset(dep,0,sizeof dep); queue<int>Q; Q.push(S);dep[S]=1; while(!Q.empty()){ int u=Q.front();Q.pop(); for(int i=head[u];~i;i=e[i].next){ if(e[i].flow&&!dep[e[i].v]){ dep[e[i].v]=dep[u]+1; Q.push(e[i].v); } } } return dep[T]; } int DFS(int u, int f){//推进新流 if(u==T||f==0)return f; int w,used=0; for(int i=head[u];~i;i=e[i].next){ if(e[i].flow&&dep[e[i].v]==dep[u]+1){ w=DFS(e[i].v,min(f,e[i].flow));//多路增广 e[i].flow-=w;e[i^1].flow+=w; used+=w;f-=w; } } if(!used)dep[u]=-1;//炸点优化 return used; } int maxflow() { int ans=0; while(BFS()){ ans+=DFS(S,inf); } return ans; } }dinic; int p; struct node{int x,y;db z;}G[N]; bool check(db k){ dinic.init(); for(int i=1;i<=m;i++){ int tmp=min(p*1.0,G[i].z/k); dinic.addedge(G[i].x,G[i].y,tmp); dinic.addedge(G[i].y,G[i].x,0); } int cur=dinic.maxflow(); // printf("k = %lf cur = %d ",k,cur); return cur>=p; } int main(){ scanf("%d %d %d",&n,&m,&p); S=1,T=n; for(int i=1;i<=m;i++){ int u,v;db f; scanf("%d %d %lf",&G[i].x,&G[i].y,&G[i].z); } db mid,l=0,r=1e12; for(int i=1;i<=100;i++){ mid=(r+l)/2; if(check(mid))l=mid; else r=mid; // printf("%.6lf ",mid); } printf("%.6lf ",l*p); // system("pause"); return 0; }
Farm Tour
POJ - 2135题意:从1走到n,再从n走到1,不能重复走一条边,求最短路。
费用流做法:源点到1连一条流量2,费用0的边,汇点到n连一条流量为2,费用为0的边,跑一遍费用流。

#include <cstdio> #include <cstring> #include <queue> #include <vector> #include <algorithm> using namespace std; typedef double db; const db eps=1e-6; const int inf=0x3f3f3f3f; const int N=1e4+5; int n,m,S,T,mincost; struct Dinic{ int head[N],dep[N],dis[N],pre[N],flow[N],last[N]; //dep记录分层图,pre点前驱,flow点的流,last点的前一条边,dis表示费用 bool inq[N]; int ecnt; struct edge{ int v,w,flow,next; }e[N*10]; void init(){ memset(head, -1, sizeof head); ecnt = 0; } void addedge(int u,int v,int w,int flow){ e[ecnt].v=v;e[ecnt].w=w;e[ecnt].flow=flow;e[ecnt].next=head[u];head[u]=ecnt++; } bool spfa(){//spfa找增广路 memset(dis,inf,sizeof dis); memset(flow,inf,sizeof flow); memset(inq,0,sizeof inq); queue<int>Q; Q.push(S);inq[S]=1;dis[S]=0;pre[T]=-1; while(!Q.empty()){ int u=Q.front();Q.pop();inq[u]=0; for(int i=head[u];~i;i=e[i].next){ int v=e[i].v,w=e[i].w; if(e[i].flow>0&&dis[v]>dis[u]+w){ dis[v]=dis[u]+w;pre[v]=u;last[v]=i; flow[v]=min(flow[u],e[i].flow); if(!inq[v]){ Q.push(v);inq[v]=1; } } } } return pre[T]!=-1; } void MCMF(){ mincost=0; while(spfa()){//推进新流 int cur=T; // maxflow+=flow[T]; mincost+=flow[T]*dis[T]; while(cur!=S){//汇点向前回溯 e[last[cur]].flow-=flow[T]; e[last[cur]^1].flow+=flow[T]; cur=pre[cur]; } } } }dinic; int main(){ scanf("%d %d",&n,&m); dinic.init(); for(int i=1,u,v,w;i<=m;i++){ scanf("%d %d %d",&u,&v,&w); dinic.addedge(u,v,w,1); dinic.addedge(v,u,-w,0); dinic.addedge(v,u,w,1); dinic.addedge(u,v,-w,0); } S=0,T=n+1; dinic.addedge(S,1,0,2); dinic.addedge(1,S,0,0); dinic.addedge(n,T,0,2); dinic.addedge(T,n,0,0); dinic.MCMF(); printf("%d ",mincost); // system("pause"); return 0; }
T123574 Voluntary Hotel
毒题;
题意:一个无向带权图里,r个医生,p个医院,q个宾馆,每个医生对应着一个医院,每个宾馆有一个容量h[ i ] ,
可以从家到医院,或者从宾馆到医院,求所有医生去上班的最大路径最小。
解法:考虑最大值最小化,二分一个d,判断在距离 d 内,所有的医生是否能走到对应的医院,
先预处理每一个点到医院的距离。
如果医生家到医院的距离小于d,无需考虑。否则都要通过宾馆而行。
将每一个宾馆与源点连一条 流量为 h [ i ] 的边,表示宾馆的人数限制,
将每个医院与汇点连一条 流量为 cnt [ i ] 的边,表示需要到该医院上班的人数限制,
for一遍每一个医院和宾馆,判断距离<=d,则宾馆和医院可以联通,两者连一条流量为 inf 的边。
最后check是否满流即可,
总复杂度O(p*q*(n^3));注意数组开大。
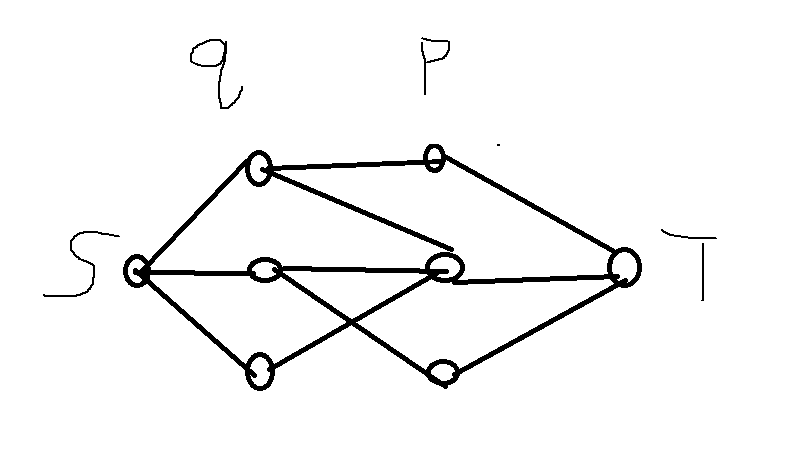

#include<bits/stdc++.h> using namespace std; #define pb push_back #define mp make_pair #define fi first #define se second typedef long long ll; const ll inf=1e15; const int N=1e6+50; int n,m,p,q,r,S,T; struct Dinic{ int head[N],dep[N]; int ecnt; struct edge{ int v; ll flow;int next; }e[N*10]; void init(){ memset(head, -1, sizeof head); ecnt = 0; } void addedge(int u, int v,ll flow) { e[ecnt].v=v;e[ecnt].flow=flow;e[ecnt].next=head[u];head[u]=ecnt++; } bool BFS(){//分层图找增广路 memset(dep,0,sizeof dep); queue<int>Q; Q.push(S);dep[S]=1; while(!Q.empty()){ int u=Q.front();Q.pop(); for(int i=head[u];~i;i=e[i].next){ if(e[i].flow&&!dep[e[i].v]){ dep[e[i].v]=dep[u]+1; Q.push(e[i].v); } } } return dep[T]; } ll DFS(int u, ll f){//推进新流 if(u==T||f==0)return f; ll w,used=0; for(int i=head[u];~i;i=e[i].next){ if(e[i].flow&&dep[e[i].v]==dep[u]+1){ w=DFS(e[i].v,min(f,e[i].flow));//多路增广 e[i].flow-=w;e[i^1].flow+=w; used+=w;f-=w; } } if(!used)dep[u]=-1;//炸点优化 return used; } ll maxflow() { ll ans=0; while(BFS()){ ans+=DFS(S,inf); } return ans; } }dinic; int X[N],Y[N],H[N],s[N],K[N]; struct edge{int v;ll w;int next;}e[N]; int ecnt,head[N]; void add(int u,int v,ll w){ e[ecnt].v=v;e[ecnt].w=w;e[ecnt].next=head[u];head[u]=ecnt++; } struct node{int id;ll dis; node(int x,ll y){id=x,dis=y;} friend bool operator<(node a,node b){ return a.dis>b.dis; } }; bool done[150][N];ll dis[150][N]; void dijkstra(int s,int k){ for(int i=1;i<=n+100;i++)dis[k][i]=inf,done[k][i]=0; dis[k][s]=0; priority_queue<node>Q; Q.push(node(s,0)); while(!Q.empty()){ int u=Q.top().id;Q.pop(); if(done[k][u])continue; done[k][u]=1; for(int i=head[u];i!=-1;i=e[i].next){ int v=e[i].v; if(done[k][v])continue; if(dis[k][v]>dis[k][u]+e[i].w){ dis[k][v]=dis[k][u]+e[i].w;//更新距离 Q.push(node(v,dis[k][v])); } } } } ll cnt[200]; bool check(ll d){ memset(cnt,0,sizeof cnt); for(int i=1;i<=r;i++)if(dis[ K[i] ][ s[i] ]>d)cnt[ K[i] ]++; ll sum=0; for(int i=1;i<=p;i++)sum+=cnt[i]; S=0,T=p+q+50;dinic.init(); for(int i=1;i<=q;i++){ dinic.addedge(S,i,H[i]); dinic.addedge(i,S,0); } for(int i=1;i<=q;i++){ for(int j=1;j<=p;j++){ if(dis[j][ Y[i] ]<=d){ dinic.addedge(i,q+j,inf); dinic.addedge(q+j,i,0); } } } for(int i=1;i<=p;i++){ dinic.addedge(q+i,T,cnt[i]); dinic.addedge(T,q+i,0); } if(dinic.maxflow()>=sum)return 1; else return 0; } int main(){ scanf("%d %d %d %d %d",&n,&m,&p,&q,&r); memset(head,-1,sizeof head);ecnt=0; for(int i=1,u,v;i<=m;i++){ ll w; scanf("%d %d %lld",&u,&v,&w); add(u,v,w);add(v,u,w); } for(int i=1;i<=p;i++)scanf("%d",&X[i]); for(int i=1;i<=p;i++)dijkstra(X[i],i); for(int i=1;i<=q;i++)scanf("%d %d",&Y[i],&H[i]); for(int i=1;i<=r;i++)scanf("%d %d",&s[i],&K[i]); ll mid,L=0,R=(ll)1e14,ans=(ll)1e14; while(L<=R){ mid=(L+R)>>1; if(check(mid))ans=mid,R=mid-1; else L=mid+1; } printf("%lld ",ans); // system("pause"); return 0; }
I - March of the Penguins
题意:给出n个岛屿,每个岛屿有ci 个企鹅,限制人数 lim i , 如果两个岛屿之间距离小于pos,那么企鹅可以相互到达,求
有多少个点可以作为终点,使得所有企鹅都可以跳到哪里。
做法:一一枚举终点,
每次建图:将 源点向所有左点连一条 ci ,表示最初有多少人,
将所有点左点和右点连一条 lim i ,表示这个点经过限制最多可以出去企鹅,
枚举每两个点,如果距离小于pos,那么 i 的右点向 j 的左点连一条 inf 的边,表示 i 经过流量限制 可以到达 j
那么 j 的右点向 i 的左点连一条 inf 的边,表示 j 经过流量限制可以到达 i
最后将枚举的 k 点的 左点 向汇点连一条inf的边,表示不经过限制可以流到汇点。
然后判断是否满流即可。

#include<cstdio> #include<algorithm> #include<queue> #include<cmath> #include<cstring> using namespace std; #define mp make_pair typedef double db; const int inf=0x3f3f3f3f; const int N=1e5+5; #define pb push_back int n,m,S,T; struct Dinic{ int head[N],dep[N]; int ecnt; struct edge{ int v,flow,next; }e[N*10]; void init(){ memset(head, -1, sizeof head); ecnt = 0; } void addedge(int u, int v, int flow) { e[ecnt].v=v;e[ecnt].flow=flow;e[ecnt].next=head[u];head[u]=ecnt++; e[ecnt].v=u;e[ecnt].flow=0;e[ecnt].next=head[v];head[v]=ecnt++; } bool BFS(){//分层图找增广路 memset(dep,0,sizeof dep); queue<int>Q; Q.push(S);dep[S]=1; while(!Q.empty()){ int u=Q.front();Q.pop(); for(int i=head[u];~i;i=e[i].next){ if(e[i].flow&&!dep[e[i].v]){ dep[e[i].v]=dep[u]+1; Q.push(e[i].v); } } } return dep[T]; } int DFS(int u, int f){//推进新流 if(u==T||f==0)return f; int w,used=0; for(int i=head[u];~i;i=e[i].next){ if(e[i].flow&&dep[e[i].v]==dep[u]+1){ w=DFS(e[i].v,min(f,e[i].flow));//多路增广 e[i].flow-=w;e[i^1].flow+=w; used+=w;f-=w; } } if(!used)dep[u]=-1;//炸点优化 return used; } int maxflow() { int ans=0; while(BFS()){ ans+=DFS(S,inf); } return ans; } }dinic; struct point{db x,y;}P[100000]; db dis(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));} int C[100000],lim[100000]; int main(){ int t; scanf("%d",&t); while(t--){ db pos; scanf("%d %lf",&n,&pos); int sum=0; for(int i=1;i<=n;i++) scanf("%lf %lf %d %d",&P[i].x,&P[i].y,&C[i],&lim[i]),sum+=C[i]; vector<int>ans; S=0,T=2*n+50; for(int k=1;k<=n;k++){ dinic.init(); for(int i=1;i<=n;i++){ dinic.addedge(S,i,C[i]); dinic.addedge(i,n+i,lim[i]); } for(int i=1;i<=n;i++){ for(int j=i+1;j<=n;j++){ if(dis(P[i],P[j])<=pos){ dinic.addedge(i+n,j,inf); dinic.addedge(j+n,i,inf); } } } dinic.addedge(k,T,inf); if(dinic.maxflow()==sum)ans.pb(k); } int len=ans.size(); if(!len){puts("-1");continue;} for(int i=0;i<len;i++){ printf("%d%c",ans[i]-1,i==len-1?' ':' '); } } // system("pause"); return 0; } // 做法应该就是枚举每一个点,当做汇点,判断是否满流
