HZNU Training 17 for Zhejiang Provincial Competition 2020

A - 2016

 CSU - 1803 

题意：给你n，m，

1. 1≤a≤n,1≤b≤m;

2. a×b 是 2016 的倍数。

求组合数。n,m (1≤n,m≤10 ⁹).

解法：暴力求解肯定是不行的，考虑如下优化：
对于在2016以内的解，a，b：

a*b%2016=0,那么(a+2016)*b%2016=0,如此类推即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll C=2016;
int main(){
    ll n,m;
    while(~scanf("%lld %lld",&n,&m)){
        ll ans=0;
        for(int i=1;i<=min(n,C);i++){
            for(int j=1;j<=min(m,C);j++){
            if((i*j)%2016==0){
                ll a=n/C+1,b=m/C+1;
                if(n%C<i)a--;
                if(m%C<j)b--;
                ans+=a*b;
            }
            }
        }
        printf("%lld
",ans);
    }
    // system("pause");
    return 0;
}

 

B - 有向无环图

 CSU - 1804 

题意：
给你一张图：求

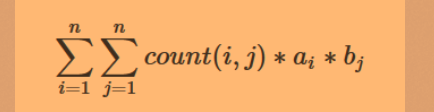
 解法：考虑如下性质：

1 传递：a如果能走到b，b能走到c，a一定可以走到c，

2.不可反：DAG，a能走到b，那么b走不到a；

于是如下解法：按拓扑序选取，把当前的值累加到下个节点。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD=1e9+7;
const int N=1e5+5;
#define pb push_back
vector<int>e[N];
int n,m;
int in[N];
ll  a[N],b[N];
ll ans;
void topo(){   
    queue<int>Q;
    for(int i=1;i<=n;i++)if(in[i]==0)Q.push(i);
    while(!Q.empty()){
        int u=Q.front();Q.pop();
        for(int i=0;i<e[u].size();i++){
            int v=e[u][i];--in[v];
        if(!in[v])Q.push(v);
        ans+=(a[u]*b[v])%MOD;ans%=MOD;
        a[v]=(a[v]+a[u])%MOD;
        }
    }
}
int main(){
    while(~scanf("%d %d",&n,&m)){
    ans=0;
    for(int i=1;i<=n;i++)e[i].clear(),in[i]=0;
    for(int i=1;i<=n;i++)scanf("%lld %lld",&a[i],&b[i]);
    for(int i=1,u,v;i<=m;i++)scanf("%d %d",&u,&v),e[u].pb(v),++in[v];
    topo();
    printf("%lld
",ans);
    }
    return 0;
}

H - Reverse

 CSU - 1810 

没意思